Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 Chuyên đề học tập của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong sách, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở mục 2 này, chúng ta sẽ cùng nhau giải quyết các bài tập liên quan đến các kiến thức đã học trong chương. Các lời giải được trình bày một cách rõ ràng, logic, kèm theo các lưu ý quan trọng để các em hiểu sâu sắc hơn về bài học.
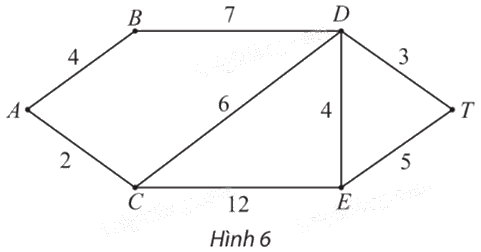
Cho đồ thị có trọng số như Hình 6.
Cho đồ thị có trọng số như Hình 6.
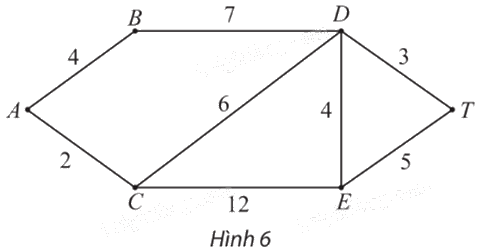
a) Tìm tất cả các đường đi từ A đến T (đi qua mỗi đỉnh nhiều nhất một lần) và tính độ dài của mỗi đường đi đó.
b) Từ đó, tìm đường đi ngắn nhất từ A đến T.
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
a) Tất cả các đường đi từ A đến T (đi qua mỗi đỉnh nhiều nhất một lần) là: ABDT, ACDT, ACET, ACDET, ACEDT, ABDET, ABDCET.
Ta có:
\({l_{ABDT}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BD}}\; + {\rm{ }}{w_{DT}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}14;\)
\(\begin{array}{l}{l_{ACDT}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CD}}\; + {\rm{ }}{w_{DT}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}11;\\\begin{array}{*{20}{l}}{{l_{ACET}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}12{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}19;}\\{{l_{ACDET}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CD}}\; + {\rm{ }}{w_{DE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}17;}\\{{l_{ACEDT}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{ED}}\; + {\rm{ }}{w_{DT}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}12{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}21;}\\{{l_{ABDET}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BD}}\; + {\rm{ }}{w_{DE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}20;}\\{{l_{ABDCET}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BD}}\; + {\rm{ }}{w_{DC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}12{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}34.}\end{array}\end{array}\)
b) Vì \(11{\rm{ }} < {\rm{ }}14{\rm{ }} < {\rm{ }}17{\rm{ }} < {\rm{ }}19{\rm{ }} < {\rm{ }}20{\rm{ }} < {\rm{ }}21{\rm{ }} < {\rm{ }}34.\)
Nên \({l_{ACDT}}\; < {\rm{ }}{l_{ABDT}}\; < {\rm{ }}{l_{ACDET}}\; < {\rm{ }}{l_{ACET}}\; < {\rm{ }}{l_{ABDET}}\; < {\rm{ }}{l_{ACEDT}}\; < {\rm{ }}{l_{ABDCET}}.\)
Vậy đường đi ngắn nhất từ A đến T là ACDT (có độ dài bằng 11).
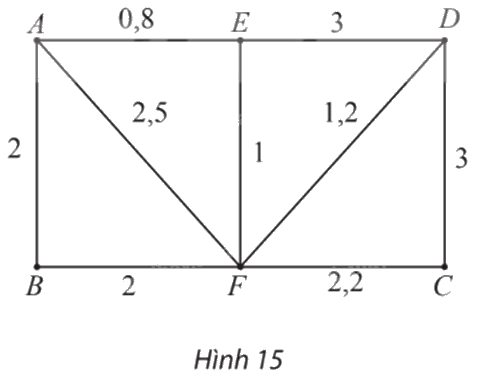
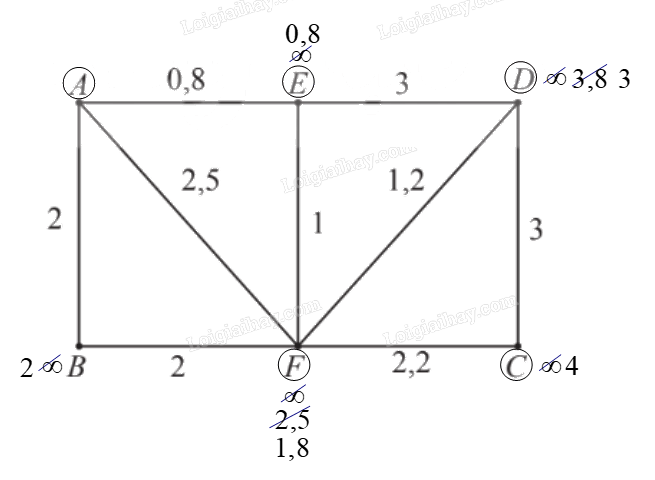
Trong đồ thị có trọng số ở Hình 15, mỗi cạnh biểu diễn một tuyến xe buýt giữa hai bến trong các bến xe A, B, C, D, E và F, trọng số của mỗi cạnh biểu diễn thời gian tính bằng giờ của tuyến xe buýt tương ứng. Một người cần ít nhất bao nhiêu thời gian để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên? Biết rằng thời gian tại bến để chuyển tiếp từ tuyến này qua tuyến kia là không đáng kể.
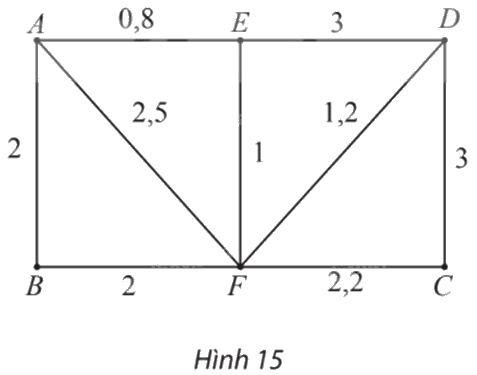
Phương pháp giải:
Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh C gọi là đường đi ngắn nhất từ A đến C.
Lời giải chi tiết:
Ta tìm khoảng thời gian ít nhất để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên bằng cách sử dụng thuật toán Dijkstra như sau:
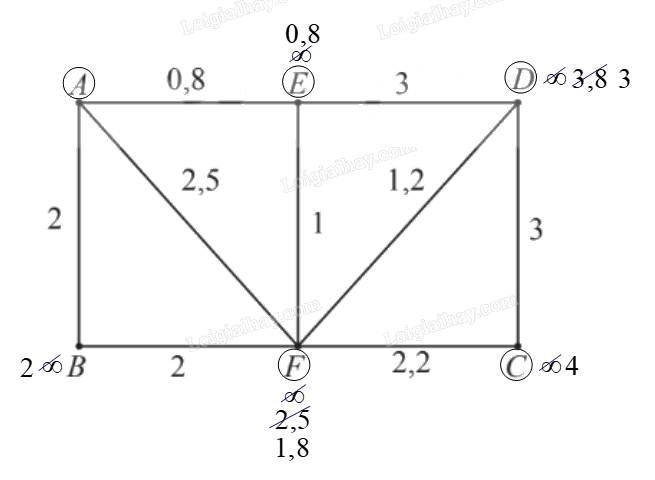
– Gán nhãn cho A bằng 0 (tức là, \({n_A}\; = {\rm{ }}0\)), các đỉnh khác bằng \(\infty \). Khoanh tròn đỉnh A.
– Tại các đỉnh kề với đỉnh A, gồm E, F, B, ta có:
⦁ \({n_E}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}0,8{\rm{ }} = {\rm{ }}0,8\).Vì \(0,8{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của E thành 0,8.
⦁ \({n_F}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AF}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}2,5{\rm{ }} = {\rm{ }}2,5\).Vì \(2,5{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của F thành 2,5.
\({n_B}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}2\).Vì \(2{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của B thành 2.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần đỉnh A nhất, chỉ tính các đỉnh khác đỉnh A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E gồm D, F, ta có:
⦁ \({n_D}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{DE}}\; = {\rm{ }}0,8{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}3,8\).Vì \(3,8{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của D thành 3,8.
⦁ \({n_F}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EF}}\; = {\rm{ }}0,8{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}1,8\).Vì \(1,8{\rm{ }} < {\rm{ }}2,5\) (2,5 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 1,8.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F gồm B, C, D, ta có:
⦁ \({n_B}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FB}}\; = {\rm{ }}1,8{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}3,8\).Vì \(3,8{\rm{ }} > {\rm{ }}2\) (2 là nhãn hiện tại của B) nên ta giữ nguyên nhãn của B là 2.
⦁ \({n_C}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FC}}\; = {\rm{ }}1,8{\rm{ }} + {\rm{ }}2,2{\rm{ }} = {\rm{ }}4\).Vì \(4{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của C thành 4.
⦁ \({n_D}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FD}}\; = {\rm{ }}1,8{\rm{ }} + {\rm{ }}1,2{\rm{ }} = {\rm{ }}3\).Vì \(3{\rm{ }} < {\rm{ }}3,8\) (3,8 là nhãn hiện tại của D) nên ta đổi nhãn của D thành 3.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B. Nhưng do trong các đỉnh chưa được khoanh tròn còn lại, ta thấy không có đỉnh nào kề với đỉnh B nên ta chọn lại đỉnh có nhãn bé nhất (ngoại trừ đỉnh B) là đỉnh D (đỉnh gần A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ còn đỉnh C, ta có:
\({n_C}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DC}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}6\).Vì \(6{\rm{ }} > {\rm{ }}4\) (4 là nhãn hiện tại của C) nên ta giữ nguyên nhãn của C là 4.
Lúc này, ngoại trừ đỉnh B, ta thấy chỉ còn đỉnh C chưa được khoanh tròn nên ta khoanh tròn đỉnh C (đỉnh gần A thứ tư).
– Nhìn ngược lại các bước trên, ta thấy:
\(\begin{array}{*{20}{l}}{{n_C}\; = {\rm{ }}4{\rm{ }} = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{l_{AEFC}}.}\end{array}\)
Vậy người đó cần ít nhất 4 giờ để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên.
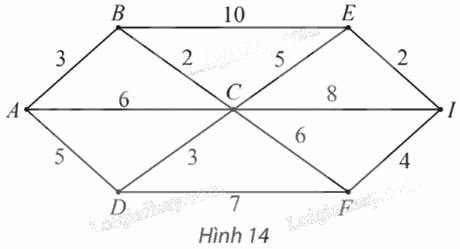
Tìm đường đi ngắn nhất từ đỉnh A đến đỉnh I trong đồ thị có trọng số ở Hình 14.
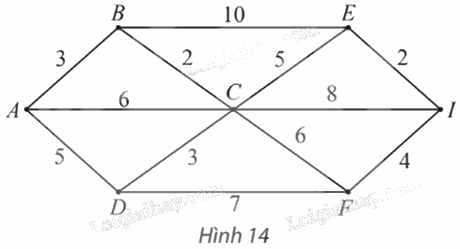
Phương pháp giải:
Tổng trọng số (hay độ dài) của các cạnh tạo thành đường đi gọi là độ dài của đường đi đó. Độ dài đường đi m kí hiệu là \({l_m}\). Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh B gọi là đường đi ngắn nhất từ A đến B
Lời giải chi tiết:

– Gán nhãn cho A bằng 0 (tức là, nA = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với A, gồm B, C, D, ta có:
⦁ \({n_B}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}3\).Vì \(3{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của B thành 3.
⦁ \({n_C}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AC}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}6\).Vì \({\rm{6 }} < {\rm{ }}\infty \) nên ta đổi nhãn của C thành 6.
⦁ \({n_D}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}5\).Vì \({\rm{5 }} < {\rm{ }}\infty \) nên ta đổi nhãn của D thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần đỉnh A nhất, chỉ tính các đỉnh khác đỉnh A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B gồm C, E, ta có:
⦁ \({n_C}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}5\).Vì \(5{\rm{ }} < {\rm{ }}6\) (6 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 5.
⦁ \({n_E}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BE}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}10{\rm{ }} = {\rm{ }}13\) .Vì \(13{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của E thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C, D (đều có nhãn là 5) nên ta tùy ý khoanh tròn đỉnh C (đỉnh gần đỉnh A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh C gồm E, D, F, I, ta có:
⦁ \({n_E}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CE}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}10\).Vì \(10{\rm{ }} < {\rm{ }}13\) (13 là nhãn hiện tại của E) nên ta đổi nhãn của E thành 10.
⦁ \({n_D}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CD}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}8\) .Vì \(8{\rm{ }} > {\rm{ }}5\) (5 là nhãn hiện tại của D) nên ta giữ nguyên nhãn của D là 5.
⦁ \({n_F}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CF}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}11\).Vì \(11{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của F thành 11.
⦁ \({n_I}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CI}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}8{\rm{ }} = {\rm{ }}13\).Vì \(13{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của I thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta khoanh tròn đỉnh D (đỉnh gần đỉnh A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ có đỉnh F, ta có:
\({n_F}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}12.\)
Vì \(12{\rm{ }} > {\rm{ }}11\) (11 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 11.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần đỉnh A thứ tư).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E chỉ có đỉnh I, ta có:
\({n_I}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EI}}\; = {\rm{ }}10{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}12.\)
Vì \(12{\rm{ }} < {\rm{ }}13\) (13 là nhãn hiện tại của I) nên ta đổi nhãn của I thành 12.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ năm).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F chỉ còn đỉnh I, ta có:
\({n_I}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FI}}\; = {\rm{ }}11{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}15.\)
Vì \(15{\rm{ }} > {\rm{ }}12\) (12 là nhãn hiện tại của I) nên ta giữ nguyên nhãn của I là 12.
Lúc này, ta thấy chỉ còn đỉnh I chưa được khoanh tròn nên ta khoanh tròn đỉnh I (đỉnh gần A thứ sáu).
– Nhìn ngược lại các bước trên, ta thấy:
\(\begin{array}{l}{n_I}\; = {\rm{ }}12{\rm{ }} = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EI}} = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}}\\ = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}}\\ = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}}\\ = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}} = {\rm{ }}{l_{ABCEI}}.\end{array}\)
Vậy ABCEI là đường đi ngắn nhất từ A đến I, với độ dài bằng 12.
Cho đồ thị có trọng số như Hình 6.
a) Tìm tất cả các đường đi từ A đến T (đi qua mỗi đỉnh nhiều nhất một lần) và tính độ dài của mỗi đường đi đó.
b) Từ đó, tìm đường đi ngắn nhất từ A đến T.
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
a) Tất cả các đường đi từ A đến T (đi qua mỗi đỉnh nhiều nhất một lần) là: ABDT, ACDT, ACET, ACDET, ACEDT, ABDET, ABDCET.
Ta có:
\({l_{ABDT}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BD}}\; + {\rm{ }}{w_{DT}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}14;\)
\(\begin{array}{l}{l_{ACDT}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CD}}\; + {\rm{ }}{w_{DT}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}11;\\\begin{array}{*{20}{l}}{{l_{ACET}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}12{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}19;}\\{{l_{ACDET}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CD}}\; + {\rm{ }}{w_{DE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}17;}\\{{l_{ACEDT}}\; = {\rm{ }}{w_{AC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{ED}}\; + {\rm{ }}{w_{DT}}\; = {\rm{ }}2{\rm{ }} + {\rm{ }}12{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}21;}\\{{l_{ABDET}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BD}}\; + {\rm{ }}{w_{DE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}4{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}20;}\\{{l_{ABDCET}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BD}}\; + {\rm{ }}{w_{DC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{ET}}\; = {\rm{ }}4{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}12{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}34.}\end{array}\end{array}\)
b) Vì \(11{\rm{ }} < {\rm{ }}14{\rm{ }} < {\rm{ }}17{\rm{ }} < {\rm{ }}19{\rm{ }} < {\rm{ }}20{\rm{ }} < {\rm{ }}21{\rm{ }} < {\rm{ }}34.\)
Nên \({l_{ACDT}}\; < {\rm{ }}{l_{ABDT}}\; < {\rm{ }}{l_{ACDET}}\; < {\rm{ }}{l_{ACET}}\; < {\rm{ }}{l_{ABDET}}\; < {\rm{ }}{l_{ACEDT}}\; < {\rm{ }}{l_{ABDCET}}.\)
Vậy đường đi ngắn nhất từ A đến T là ACDT (có độ dài bằng 11).
Tìm đường đi ngắn nhất từ đỉnh A đến đỉnh I trong đồ thị có trọng số ở Hình 14.
Phương pháp giải:
Tổng trọng số (hay độ dài) của các cạnh tạo thành đường đi gọi là độ dài của đường đi đó. Độ dài đường đi m kí hiệu là \({l_m}\). Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh B gọi là đường đi ngắn nhất từ A đến B
Lời giải chi tiết:

– Gán nhãn cho A bằng 0 (tức là, nA = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với A, gồm B, C, D, ta có:
⦁ \({n_B}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}3\).Vì \(3{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của B thành 3.
⦁ \({n_C}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AC}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}6\).Vì \({\rm{6 }} < {\rm{ }}\infty \) nên ta đổi nhãn của C thành 6.
⦁ \({n_D}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}5\).Vì \({\rm{5 }} < {\rm{ }}\infty \) nên ta đổi nhãn của D thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần đỉnh A nhất, chỉ tính các đỉnh khác đỉnh A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B gồm C, E, ta có:
⦁ \({n_C}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}5\).Vì \(5{\rm{ }} < {\rm{ }}6\) (6 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 5.
⦁ \({n_E}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BE}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}10{\rm{ }} = {\rm{ }}13\) .Vì \(13{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của E thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C, D (đều có nhãn là 5) nên ta tùy ý khoanh tròn đỉnh C (đỉnh gần đỉnh A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh C gồm E, D, F, I, ta có:
⦁ \({n_E}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CE}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}10\).Vì \(10{\rm{ }} < {\rm{ }}13\) (13 là nhãn hiện tại của E) nên ta đổi nhãn của E thành 10.
⦁ \({n_D}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CD}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}8\) .Vì \(8{\rm{ }} > {\rm{ }}5\) (5 là nhãn hiện tại của D) nên ta giữ nguyên nhãn của D là 5.
⦁ \({n_F}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CF}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}11\).Vì \(11{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của F thành 11.
⦁ \({n_I}\; = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CI}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}8{\rm{ }} = {\rm{ }}13\).Vì \(13{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của I thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta khoanh tròn đỉnh D (đỉnh gần đỉnh A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ có đỉnh F, ta có:
\({n_F}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}12.\)
Vì \(12{\rm{ }} > {\rm{ }}11\) (11 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 11.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần đỉnh A thứ tư).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E chỉ có đỉnh I, ta có:
\({n_I}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EI}}\; = {\rm{ }}10{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}12.\)
Vì \(12{\rm{ }} < {\rm{ }}13\) (13 là nhãn hiện tại của I) nên ta đổi nhãn của I thành 12.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ năm).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F chỉ còn đỉnh I, ta có:
\({n_I}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FI}}\; = {\rm{ }}11{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}15.\)
Vì \(15{\rm{ }} > {\rm{ }}12\) (12 là nhãn hiện tại của I) nên ta giữ nguyên nhãn của I là 12.
Lúc này, ta thấy chỉ còn đỉnh I chưa được khoanh tròn nên ta khoanh tròn đỉnh I (đỉnh gần A thứ sáu).
– Nhìn ngược lại các bước trên, ta thấy:
\(\begin{array}{l}{n_I}\; = {\rm{ }}12{\rm{ }} = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EI}} = {\rm{ }}{n_C}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}}\\ = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}}\\ = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}}\\ = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CE}}\; + {\rm{ }}{w_{EI}} = {\rm{ }}{l_{ABCEI}}.\end{array}\)
Vậy ABCEI là đường đi ngắn nhất từ A đến I, với độ dài bằng 12.
Trong đồ thị có trọng số ở Hình 15, mỗi cạnh biểu diễn một tuyến xe buýt giữa hai bến trong các bến xe A, B, C, D, E và F, trọng số của mỗi cạnh biểu diễn thời gian tính bằng giờ của tuyến xe buýt tương ứng. Một người cần ít nhất bao nhiêu thời gian để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên? Biết rằng thời gian tại bến để chuyển tiếp từ tuyến này qua tuyến kia là không đáng kể.
Phương pháp giải:
Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh C gọi là đường đi ngắn nhất từ A đến C.
Lời giải chi tiết:
Ta tìm khoảng thời gian ít nhất để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên bằng cách sử dụng thuật toán Dijkstra như sau:
– Gán nhãn cho A bằng 0 (tức là, \({n_A}\; = {\rm{ }}0\)), các đỉnh khác bằng \(\infty \). Khoanh tròn đỉnh A.
– Tại các đỉnh kề với đỉnh A, gồm E, F, B, ta có:
⦁ \({n_E}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}0,8{\rm{ }} = {\rm{ }}0,8\).Vì \(0,8{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của E thành 0,8.
⦁ \({n_F}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AF}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}2,5{\rm{ }} = {\rm{ }}2,5\).Vì \(2,5{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của F thành 2,5.
\({n_B}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}2\).Vì \(2{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của B thành 2.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần đỉnh A nhất, chỉ tính các đỉnh khác đỉnh A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E gồm D, F, ta có:
⦁ \({n_D}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{DE}}\; = {\rm{ }}0,8{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}3,8\).Vì \(3,8{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của D thành 3,8.
⦁ \({n_F}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EF}}\; = {\rm{ }}0,8{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}1,8\).Vì \(1,8{\rm{ }} < {\rm{ }}2,5\) (2,5 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 1,8.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F gồm B, C, D, ta có:
⦁ \({n_B}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FB}}\; = {\rm{ }}1,8{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}3,8\).Vì \(3,8{\rm{ }} > {\rm{ }}2\) (2 là nhãn hiện tại của B) nên ta giữ nguyên nhãn của B là 2.
⦁ \({n_C}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FC}}\; = {\rm{ }}1,8{\rm{ }} + {\rm{ }}2,2{\rm{ }} = {\rm{ }}4\).Vì \(4{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của C thành 4.
⦁ \({n_D}\; = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FD}}\; = {\rm{ }}1,8{\rm{ }} + {\rm{ }}1,2{\rm{ }} = {\rm{ }}3\).Vì \(3{\rm{ }} < {\rm{ }}3,8\) (3,8 là nhãn hiện tại của D) nên ta đổi nhãn của D thành 3.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B. Nhưng do trong các đỉnh chưa được khoanh tròn còn lại, ta thấy không có đỉnh nào kề với đỉnh B nên ta chọn lại đỉnh có nhãn bé nhất (ngoại trừ đỉnh B) là đỉnh D (đỉnh gần A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ còn đỉnh C, ta có:
\({n_C}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DC}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}6\).Vì \(6{\rm{ }} > {\rm{ }}4\) (4 là nhãn hiện tại của C) nên ta giữ nguyên nhãn của C là 4.
Lúc này, ngoại trừ đỉnh B, ta thấy chỉ còn đỉnh C chưa được khoanh tròn nên ta khoanh tròn đỉnh C (đỉnh gần A thứ tư).
– Nhìn ngược lại các bước trên, ta thấy:
\(\begin{array}{*{20}{l}}{{n_C}\; = {\rm{ }}4{\rm{ }} = {\rm{ }}{n_F}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EF}}\; + {\rm{ }}{w_{FC}}}\\{ = {\rm{ }}{l_{AEFC}}.}\end{array}\)
Vậy người đó cần ít nhất 4 giờ để di chuyển từ bến A đến bến C bằng xe buýt của các tuyến trên.
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Các bài tập trong mục này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khảo sát hàm số.
Chúng ta sẽ đi vào giải chi tiết từng bài tập từ trang 61 đến trang 65:
Để giải quyết hiệu quả các bài tập trong mục 2, các em cần nắm vững các phương pháp sau:
Ví dụ: Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Giải:
Trong quá trình giải bài tập, các em cần lưu ý:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết các bài tập trong mục 2 trang 61, 62, 63, 64, 65 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!