Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 7 trang 19, giúp bạn hiểu rõ phương pháp và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin chinh phục môn Toán.
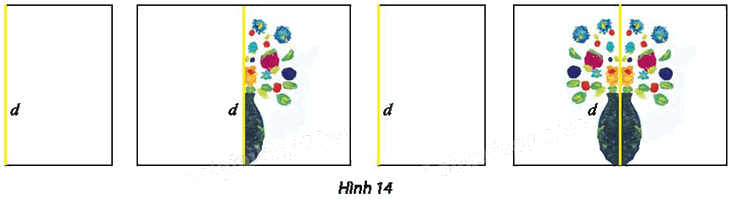
Vận dụng phép đối xứng trục để vẽ nhanh bình hoa theo hướng dẫn trong Hình 14.
Đề bài
Vận dụng phép đối xứng trục để vẽ nhanh bình hoa theo hướng dẫn trong Hình 14.
– Gấp đôi một tờ giấy trắng A4 theo nếp gấp d.
– Mở tờ giấy ra, ở một phía của nếp gấp d, nhỏ vài giọt màu nước có màu khác nhau làm hoa và một giọt màu đen làm bình hoa.
– Gấp lại tờ giấy theo nếp gấp d, chà nhẹ để màu thấm đều sang hai bên.
– Mở tờ giấy ra, ta có một bình hoa đẹp.
Tìm trục đối xứng của hình vừa vẽ.
Phương pháp giải - Xem chi tiết
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết

Lấy điểm A nằm trên hình bình hoa vừa vẽ nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên hình bình hoa vừa vẽ.
Lấy điểm B nằm trên hình bình hoa vừa vẽ và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình bình hoa vừa vẽ, ta đều xác định được ảnh của các điểm đó qua Đd trên hình bình hoa vừa vẽ.
Do đó \({Đ_d}\) biến hình bình hoa vừa vẽ thành chính nó.
Vậy đường thẳng d là trục đối xứng của hình bình hoa vừa vẽ.
Bài 7 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài, xác định rõ yêu cầu và các thông tin đã cho. Sau đó, cần lựa chọn phương pháp giải phù hợp, dựa trên kiến thức đã học và đặc điểm của bài toán. Một số phương pháp thường được sử dụng để giải bài tập về hàm số bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 7 trang 19. Giả sử bài 7 yêu cầu chúng ta xét hàm số f(x) = x3 - 3x2 + 2:
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là R (tập hợp tất cả các số thực).
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy x = 0 hoặc x = 2
Xét dấu f'(x) trên các khoảng:
Vậy hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Dựa vào các thông tin đã phân tích, ta có thể vẽ đồ thị hàm số f(x) = x3 - 3x2 + 2. Đồ thị hàm số có dạng đường cong đi qua các điểm cực trị và có tính đối xứng qua điểm uốn.
Khi giải bài tập về hàm số, cần chú ý các điểm sau:
Kiến thức về hàm số có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Bài 7 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin giải quyết bài tập này và các bài tập tương tự.