Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O bán kính R = 9 và cho điểm A khác O.
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O bán kính R = 9 và cho điểm A khác O. Gọi (C’) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow {OA} \) và phép vị tự \({V_{\left( {O; - \frac{1}{3}} \right)}}\). Tìm diện tích hình tròn (C’).
Phương pháp giải - Xem chi tiết
Diện tích hình tròn \(S = \pi {R^2}\), R là bán kính hình tròn.
Lời giải chi tiết
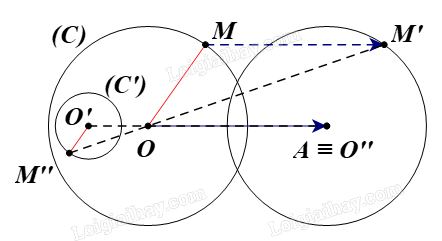
Phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo \(\overrightarrow {OA} \) và phép vị tự \({V_{\left( {O; - \frac{1}{3}} \right)}}\) biến đường tròn (C) thành đường tròn (C’).
Suy ra phép đồng dạng đó có tỉ số là \(k = \left| { - \frac{1}{3}} \right| = \frac{1}{3}\)
Đường tròn (C’) có tâm O’, bán kính R’.
Suy ra O’ là ảnh của O qua phép đồng dạng tỉ số \(\frac{1}{3}\)
Gọi M là điểm bất kì nằm trên đường tròn (C).
Suy ra M’ là ảnh của M qua phép đồng dạng tỉ số \(\frac{1}{3}\)
Khi đó ta có \(O'M' = \frac{1}{3}OM\)
Vì vậy \(R' = \frac{1}{3}R = \frac{1}{3}.9 = 3\)
Diện tích hình tròn (C’) là: \({S_{(C')}} = \pi R{'^2} = \pi {3^2} = 9\pi \)
Vậy diện tích hình tròn (C’) là \(9\pi \).
Bài 3 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải có sự hiểu biết sâu sắc về lý thuyết và khả năng áp dụng linh hoạt các công thức, định lý đã học.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải bài 3 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ: Cho hàm số y = x2 - 4x + 3. Hãy xác định tập xác định, tập giá trị, tìm điểm cực trị và vẽ đồ thị hàm số.
Giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các trang web học toán online.
Học Toán 11 đòi hỏi sự kiên trì và nỗ lực. Hãy dành thời gian ôn tập lý thuyết, làm bài tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| y = ax2 + bx + c | Hàm số bậc hai |
| x = -b/2a | Hoành độ đỉnh của parabol |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |