Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11 Chuyên đề học tập. Bài viết này sẽ hướng dẫn bạn giải quyết bài 8 trang 68 một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
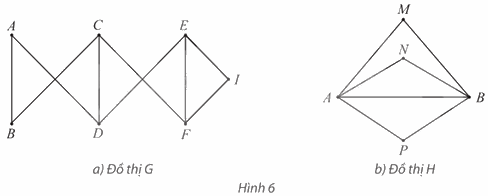
Mỗi đồ thị trong Hình 6 có chu trình Hamilton không? Nếu có hãy chỉ ra một chu trình như vậy.
Đề bài
Mỗi đồ thị trong Hình 6 có chu trình Hamilton không? Nếu có hãy chỉ ra một chu trình như vậy. Nếu không, đồ thị có đường đi Hamilton không? Nếu có, hãy chỉ ra một đường đi như vậy.
Phương pháp giải - Xem chi tiết
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton.
Lời giải chi tiết
a) Đồ thị G:
Đồ thị G có các đỉnh A, B, I có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh AB, AD, BC, EI, FI.
Do đó ta có một chu trình Hamilton h của đồ thị G là: CBADEIFC.
b) Đồ thị H:
Đồ thị H có các đỉnh M, N, P có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh MA, MB, NA, NB, PA, PB.
Ta thấy chu trình Hamilton h (nếu có) đi qua ba cạnh MA, NA, PA nối với đỉnh A nên chu trình Hamilton h không tồn tại.
Đồ thị H có đường đi Hamilton, chẳng hạn MANBP.
Vậy đồ thị G không có chu trình Hamilton và cũng không có đường đi Hamilton; đồ thị H không có chu trình Hamilton và có đường đi Hamilton.
Bài 8 trang 68 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 8 trang 68, chúng tôi sẽ cung cấp lời giải chi tiết cho từng dạng bài tập. Dưới đây là một ví dụ minh họa:
Cho hàm số y = f(x) = (x2 + 1)3. Hãy tính đạo hàm f'(x).
Lời giải:
Áp dụng quy tắc đạo hàm hàm hợp, ta có:
f'(x) = 3(x2 + 1)2 * (2x) = 6x(x2 + 1)2
Để học tốt môn Toán 11, bạn nên:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 8 trang 68 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các lời khuyên hữu ích trên đây, bạn sẽ tự tin hơn trong việc giải quyết bài tập này và đạt kết quả tốt trong môn Toán 11.
| Công thức | Mô tả |
|---|---|
| (u + v)' | Đạo hàm của tổng hai hàm số |
| (u - v)' | Đạo hàm của hiệu hai hàm số |
| (u * v)' | Đạo hàm của tích hai hàm số |