Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 79 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Phác họa hình chiếu vuông góc của:
Đề bài
Phác họa hình chiếu vuông góc của:
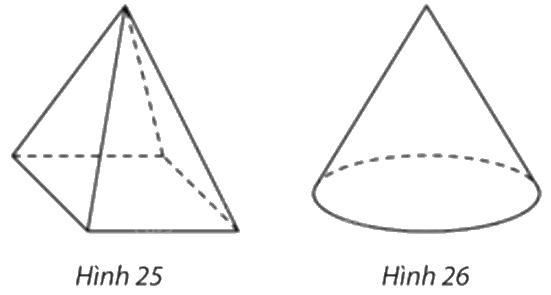
a) Khối chóp tứ giác đều (Hình 25).
b) Khối nón tròn xoay (Hình 26).
Phương pháp giải - Xem chi tiết
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết
a) Hình chiếu vuông góc của khối chóp tứ giác đều ở Hình 25 được biểu diễn trên bản vẽ như sau:

b) Hình chiếu vuông góc của khối nón tròn xoay ở Hình 26 được biểu diễn trên bản vẽ như sau:

Bài 1 trang 79 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 1 thường xoay quanh việc xét tính đơn điệu của hàm số. Cụ thể, học sinh cần:
Để giải bài 1 trang 79 Chuyên đề học tập Toán 11 Chân trời sáng tạo, chúng ta sẽ thực hiện các bước sau:
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2. Ta tính đạo hàm f'(x) như sau:
f'(x) = 3x2 - 6x
Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Dựa vào bảng biến thiên, ta có thể kết luận:
Việc giải bài 1 trang 79 Chuyên đề học tập Toán 11 Chân trời sáng tạo không chỉ giúp học sinh hiểu rõ về tính đơn điệu của hàm số mà còn là nền tảng để giải quyết các bài toán phức tạp hơn liên quan đến cực trị, khoảng đồng biến, nghịch biến và ứng dụng của đạo hàm trong các lĩnh vực khác.
Để học tập và ôn luyện môn Toán 11 hiệu quả, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã có thể tự tin giải bài 1 trang 79 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!