Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục kiến thức.
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).
Đề bài
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).
a) Tìm ảnh của A qua \({Đ_{Ox}}\) và ảnh của B qua \({Đ_{Oy}}\).
b) Biết M là ảnh của N qua \({Đ_{Oy}}\). Xác định tọa độ của N.
Phương pháp giải - Xem chi tiết
Nếu \(M' = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu\(M' = {Đ_{Oy}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết
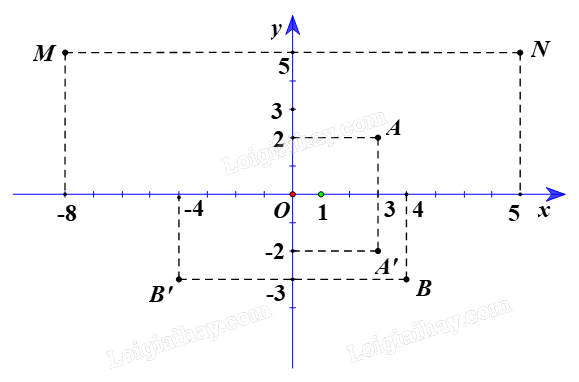
a)
+ Gọi A’ là ảnh của A qua \({Đ_{Ox}}\).
Suy ra Ox là đường trung trực của đoạn AA’ hay A’ đối xứng với A qua Ox
Do đó hai điểm A(3; 2) và A’ có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ điểm A’(3; –2).
+ Gọi B’ là ảnh của B qua \({Đ_{Oy}}\).
Suy ra Oy là đường trung trực của đoạn BB’ hay B’ đối xứng với B qua Oy
Do đó hai điểm B(4; –3) và B’ có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm B’(–4; –3).
Vậy ảnh của A qua \({Đ_{Ox}}\) là A’(3; –2) và ảnh của B qua \({Đ_{Oy}}\) là B’(–4; –3).
b) Ta có M là ảnh của N qua \({Đ_{Oy}}\)
Suy ra Oy là đường trung trực của đoạn MN hay M và N đối xứng với nhau qua Oy
Do đó hai điểm M(–8; 5) và N có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm N(8; 5).
Vậy tọa độ N(8; 5).
Bài 3 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm cơ bản, nắm vững các phương pháp giải và có khả năng áp dụng linh hoạt vào thực tế.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 3 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ: Cho hàm số y = x2 - 4x + 3. Hãy xác định tập xác định, tập giá trị, xét tính đơn điệu và vẽ đồ thị của hàm số.
Giải:
Khi giải bài 3 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo, học sinh cần lưu ý:
Để học tập và ôn luyện kiến thức về hàm số và đồ thị hàm số, học sinh có thể tham khảo các tài liệu sau:
Bài 3 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và đồ thị hàm số. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán.