Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 75, 76, 77, 78, 79 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập.
Bài giải này được xây dựng bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và phù hợp với chương trình học.
Cho hình hộp chữ nhật (OABC.{O_1}{A_1}{B_1}{C_1}.)
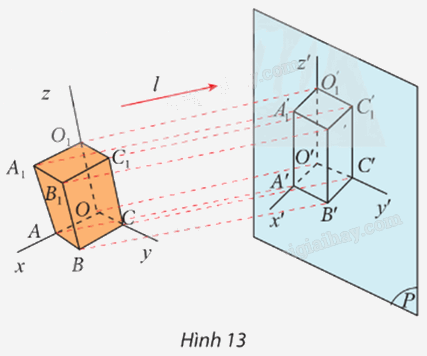
Cho hình hộp chữ nhật \(OABC.{O_1}{A_1}{B_1}{C_1}.\) Ba tia Ox, Oy, Oz lần lượt chứa ba cạnh OA, OC, OO1. Cho mặt phẳng (P) và đường thẳng l không song song với (P). Tìm ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
Phương pháp giải:
Để tìm ảnh của hình ta tìm ảnh của từng điểm qua phép chiếu song song theo phương l lên mặt phẳng (P).
Lời giải chi tiết:
– Ta có OO’ // l và \(O' \in \left( P \right).\)
Suy ra O’ là ảnh của O qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được A’, B’, C’, lần lượt là ảnh của A, B, C, O1, A1, B1, C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
Do đó là ảnh của hình hộp chữ nhật OABC.O1A1B1C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
– Ta có O’, A’ lần lượt là ảnh của O, A qua phép chiếu song song theo phương l lên mặt phẳng (P).
Suy ra O’A’ là ảnh của OA qua phép chiếu song song theo phương l lên mặt phẳng (P).
Mà A’ ∈ O’x’.
Do đó O’x’ là ảnh của Ox qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được O’y’, O’z’ lần lượt là ảnh của Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
Vậy ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P) lần lượt là hình hộp chữ nhật và các tia O’x’, O’y’, O’z’.
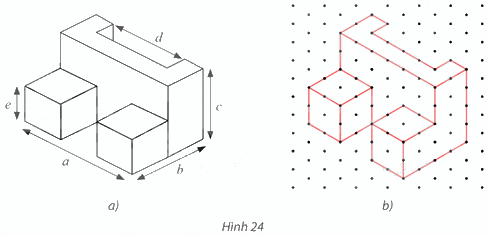
Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a có hình biểu diễn được vẽ trên giấy kẻ ô li là Hình 24b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm.
Phương pháp giải:
Quan sát hình 24 để trả lời
Lời giải chi tiết:
Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a được biểu diễn trên Hình 24b như sau:
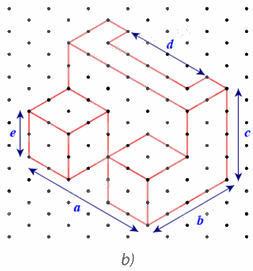
Do mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm nên ta có:
Chiều dài a = 6 cm; chiều rộng b = 4 cm; chiều cao c = 4 cm; bề dày d = 4 cm; bề dày e = 2 cm.
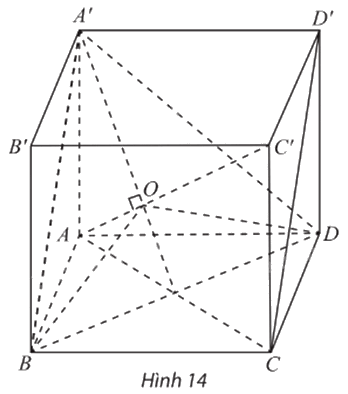
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng đơn vị (Hình 14).
a) Chỉ ra rằng \(AC' \bot \left( {A'BD} \right).\)
b) Gọi O là tâm của tam giác đều A’BD. Hình chiếu vuông góc của ba đoạn AB, AD và AA’ lên (A’BD) có bằng nhau không?
c) Chỉ ra rằng \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
Phương pháp giải:
Để chứng minh đường thẳng \(d \bot (P)\) ta chứng minh d vuông góc với 2 đường thẳng cắt nhau nằm trong (P).
Lời giải chi tiết:
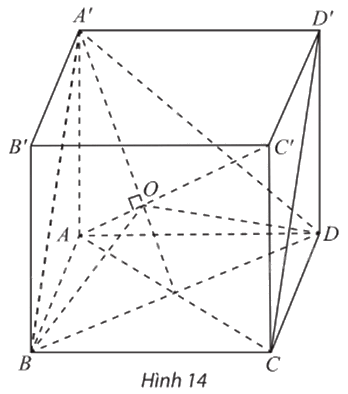
a) Ta có \(A'D \bot AD'\) (AA’D’D là hình vuông) và \(A'D \bot C'D'{\rm{ }}(C'D' \bot \left( {AA'D'D} \right)).\) Suy ra \(A'D \bot \left( {AC'D'} \right).\)
Do đó \(A'D \bot AC'{\rm{ }}\left( 1 \right)\)
Chứng minh tương tự, ta được \(A'B \bot AC'{\rm{ }}\left( 2 \right)\)
Từ (1), (2), ta thu được \(AC' \bot \left( {A'BD} \right).\)
b) Gọi M là trung điểm BD.
Ta có AB = AD (do ABCD là hình vuông).
Suy ra tam giác ABD cân tại A.
Do đó AM ⊥ BD.
Lại có O là tâm của tam giác đều A’BD.
Suy ra \(A'M \bot BD\) và \(O \in A'M\).
Ta có \(AM \bot BD\) và \(A'M \bot BD\) (chứng minh trên).
Suy ra \(BD \bot \left( {AA'M} \right).\)
Do đó \(BD \bot AO{\rm{ }}\left( 3 \right)\)
Chứng minh tương tự, ta được \(A'D \bot AO{\rm{ }}\left( 4 \right)\)
Từ (3), (4), suy ra \(AO \bot \left( {A'BD} \right).\)
Khi đó O là hình chiếu vuông góc của A lên mặt phẳng (A’BD).
Mà B là hình chiếu vuông góc của B lên mặt phẳng (A’BD).
Suy ra OB là hình chiếu vuông góc của AB lên mặt phẳng (A’BD).
Chứng minh tương tự, ta được: OD, OA’ lần lượt là hình chiếu vuông góc của AD, AA’ lên mặt phẳng (A’BD).
Tam giác A’BD đều có tâm O.
Suy ra OA’ = OB = OD.
Vậy hình chiếu vuông góc OB, OD và OA’ lần lượt của ba đoạn AB, AD và AA’ lên (A’BD) có độ dài bằng nhau.
c) Ta có tam giác A’BD đều. Suy ra \(\widehat {BA'D} = 60^\circ \)
Tam giác A’BD đều có tâm O. Suy ra O là tâm đường tròn ngoại tiếp tam giác A’BD.
Khi đó \(\widehat {BOD} = 2\widehat {BA'D} = 2.60^\circ = 120^\circ \)
Chứng minh tương tự, ta được \(\widehat {DOA'} = 120^\circ \) và \(\widehat {A'OB} = 120^\circ \)
Vậy \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
Cho hình hộp chữ nhật \(OABC.{O_1}{A_1}{B_1}{C_1}.\) Ba tia Ox, Oy, Oz lần lượt chứa ba cạnh OA, OC, OO1. Cho mặt phẳng (P) và đường thẳng l không song song với (P). Tìm ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
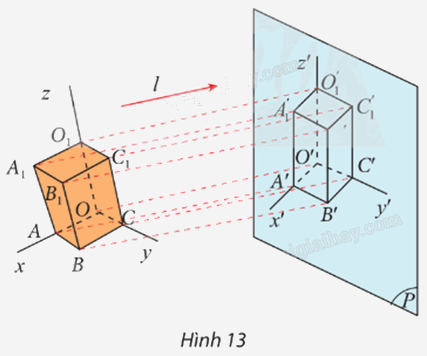
Phương pháp giải:
Để tìm ảnh của hình ta tìm ảnh của từng điểm qua phép chiếu song song theo phương l lên mặt phẳng (P).
Lời giải chi tiết:
– Ta có OO’ // l và \(O' \in \left( P \right).\)
Suy ra O’ là ảnh của O qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được A’, B’, C’, lần lượt là ảnh của A, B, C, O1, A1, B1, C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
Do đó là ảnh của hình hộp chữ nhật OABC.O1A1B1C1 qua phép chiếu song song theo phương l lên mặt phẳng (P).
– Ta có O’, A’ lần lượt là ảnh của O, A qua phép chiếu song song theo phương l lên mặt phẳng (P).
Suy ra O’A’ là ảnh của OA qua phép chiếu song song theo phương l lên mặt phẳng (P).
Mà A’ ∈ O’x’.
Do đó O’x’ là ảnh của Ox qua phép chiếu song song theo phương l lên mặt phẳng (P).
Chứng minh tương tự, ta được O’y’, O’z’ lần lượt là ảnh của Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).
Vậy ảnh của hình hộp chữ nhật OABC.O1A1B1C1 và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P) lần lượt là hình hộp chữ nhật và các tia O’x’, O’y’, O’z’.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng đơn vị (Hình 14).
a) Chỉ ra rằng \(AC' \bot \left( {A'BD} \right).\)
b) Gọi O là tâm của tam giác đều A’BD. Hình chiếu vuông góc của ba đoạn AB, AD và AA’ lên (A’BD) có bằng nhau không?
c) Chỉ ra rằng \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
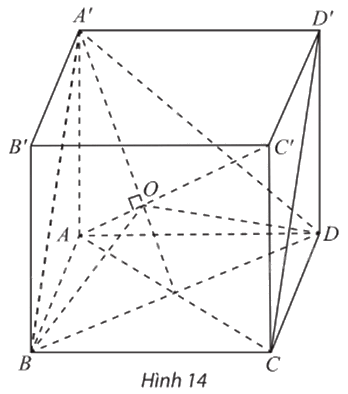
Phương pháp giải:
Để chứng minh đường thẳng \(d \bot (P)\) ta chứng minh d vuông góc với 2 đường thẳng cắt nhau nằm trong (P).
Lời giải chi tiết:
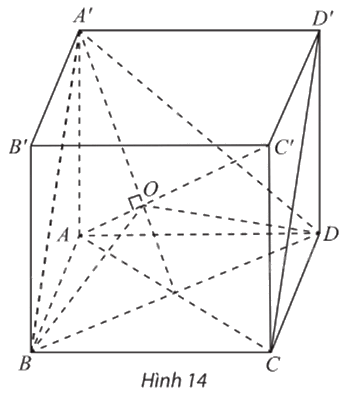
a) Ta có \(A'D \bot AD'\) (AA’D’D là hình vuông) và \(A'D \bot C'D'{\rm{ }}(C'D' \bot \left( {AA'D'D} \right)).\) Suy ra \(A'D \bot \left( {AC'D'} \right).\)
Do đó \(A'D \bot AC'{\rm{ }}\left( 1 \right)\)
Chứng minh tương tự, ta được \(A'B \bot AC'{\rm{ }}\left( 2 \right)\)
Từ (1), (2), ta thu được \(AC' \bot \left( {A'BD} \right).\)
b) Gọi M là trung điểm BD.
Ta có AB = AD (do ABCD là hình vuông).
Suy ra tam giác ABD cân tại A.
Do đó AM ⊥ BD.
Lại có O là tâm của tam giác đều A’BD.
Suy ra \(A'M \bot BD\) và \(O \in A'M\).
Ta có \(AM \bot BD\) và \(A'M \bot BD\) (chứng minh trên).
Suy ra \(BD \bot \left( {AA'M} \right).\)
Do đó \(BD \bot AO{\rm{ }}\left( 3 \right)\)
Chứng minh tương tự, ta được \(A'D \bot AO{\rm{ }}\left( 4 \right)\)
Từ (3), (4), suy ra \(AO \bot \left( {A'BD} \right).\)
Khi đó O là hình chiếu vuông góc của A lên mặt phẳng (A’BD).
Mà B là hình chiếu vuông góc của B lên mặt phẳng (A’BD).
Suy ra OB là hình chiếu vuông góc của AB lên mặt phẳng (A’BD).
Chứng minh tương tự, ta được: OD, OA’ lần lượt là hình chiếu vuông góc của AD, AA’ lên mặt phẳng (A’BD).
Tam giác A’BD đều có tâm O.
Suy ra OA’ = OB = OD.
Vậy hình chiếu vuông góc OB, OD và OA’ lần lượt của ba đoạn AB, AD và AA’ lên (A’BD) có độ dài bằng nhau.
c) Ta có tam giác A’BD đều. Suy ra \(\widehat {BA'D} = 60^\circ \)
Tam giác A’BD đều có tâm O. Suy ra O là tâm đường tròn ngoại tiếp tam giác A’BD.
Khi đó \(\widehat {BOD} = 2\widehat {BA'D} = 2.60^\circ = 120^\circ \)
Chứng minh tương tự, ta được \(\widehat {DOA'} = 120^\circ \) và \(\widehat {A'OB} = 120^\circ \)
Vậy \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)
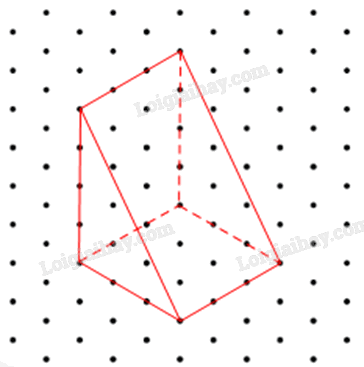
Vẽ trên giấy kẻ ô li hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 (quy tắc mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm).
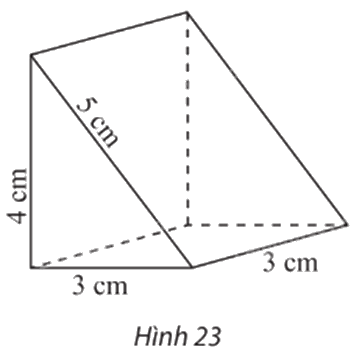
Phương pháp giải:
Hình biểu diễn của một hình khối H trong không gian là hình chiếu song song hoặc vuông góc của H lên mặt phẳng.
Lời giải chi tiết:
Hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 là:

Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a có hình biểu diễn được vẽ trên giấy kẻ ô li là Hình 24b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm.
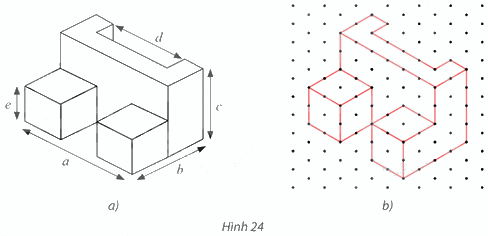
Phương pháp giải:
Quan sát hình 24 để trả lời
Lời giải chi tiết:
Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a được biểu diễn trên Hình 24b như sau:
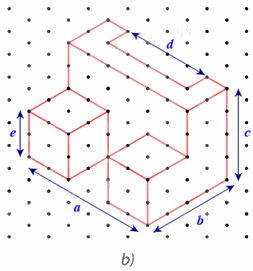
Do mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm nên ta có:
Chiều dài a = 6 cm; chiều rộng b = 4 cm; chiều cao c = 4 cm; bề dày d = 4 cm; bề dày e = 2 cm.
Vẽ trên giấy kẻ ô li hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 (quy tắc mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm).
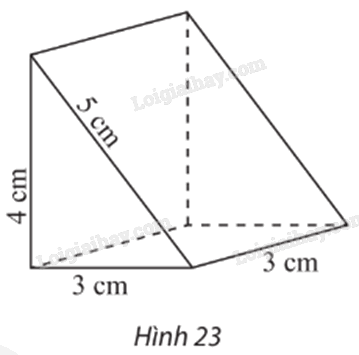
Phương pháp giải:
Hình biểu diễn của một hình khối H trong không gian là hình chiếu song song hoặc vuông góc của H lên mặt phẳng.
Lời giải chi tiết:
Hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 là:
Mục 3 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số lượng giác. Đây là một phần quan trọng trong chương trình Toán 11, đòi hỏi học sinh phải nắm vững các công thức và kỹ năng tính đạo hàm. Việc giải các bài tập trong mục này sẽ giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán.
Các bài tập trang 75 chủ yếu tập trung vào việc tính đạo hàm của các hàm số lượng giác cơ bản như sin(x), cos(x), tan(x), cot(x). Các em cần áp dụng các công thức đạo hàm đã học để giải quyết các bài tập này. Ví dụ:
Trang 76 giới thiệu các bài tập về đạo hàm của tổng, hiệu, tích, thương của các hàm số lượng giác. Các em cần sử dụng các quy tắc đạo hàm để giải quyết các bài tập này. Ví dụ:
Các bài tập trang 77 tập trung vào việc tính đạo hàm của hàm hợp. Các em cần sử dụng quy tắc đạo hàm của hàm hợp để giải quyết các bài tập này. Ví dụ:
Trang 78 giới thiệu các bài tập về đạo hàm cấp hai của hàm số lượng giác. Các em cần tính đạo hàm cấp nhất trước, sau đó tính đạo hàm của đạo hàm cấp nhất để được đạo hàm cấp hai. Ví dụ:
Các bài tập trang 79 là các bài tập tổng hợp, kết hợp các kiến thức đã học về đạo hàm của hàm số lượng giác. Các em cần vận dụng linh hoạt các công thức và quy tắc đạo hàm để giải quyết các bài tập này. Ví dụ:
Đạo hàm hàm số lượng giác có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về đạo hàm hàm số lượng giác và tự tin giải các bài tập trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!