Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 39, 40 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chuyên đề học tập Toán 11 - Chân trời sáng tạo là một tài liệu quan trọng, giúp các em củng cố và nâng cao kiến thức.
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
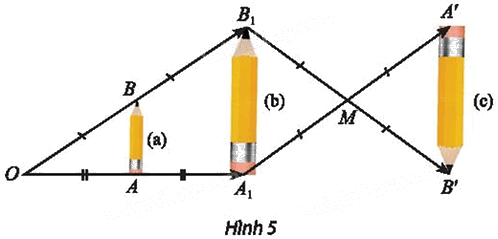
Tìm các cặp hình đồng dạng với nhau có trong Hình 5.
Phương pháp giải:
Quan sát hình 5 để tìm các cặp hình đồng dạng
Lời giải chi tiết:
⦁ Xét cặp hình (a) và (b):
Ta có \(O{A_1}\; = {\rm{ }}2OA\) và \(\overrightarrow {O{A_1}} \;,\,\overrightarrow {OA} \) cùng phương.
Suy ra \(\overrightarrow {O{A_1}} = 2\,\overrightarrow {OA} \)
Do đó \({V_{\left( {O,{\rm{ }}2} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Chứng minh tương tự, ta được \({V_{\left( {O,{\rm{ }}2} \right)}}\left( B \right){\rm{ }} = {\rm{ }}{B_1}.\)
Vì vậy \({V_{\left( {O,{\rm{ }}2} \right)}}\left( {AB} \right){\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Khi đó \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) biến hình (a) thành hình (b).
Vì vậy phép đồng dạng tỉ số 2 biến hình (a) thành hình (b).
Do đó hình (a) và hình (b) đồng dạng với nhau.
⦁ Ta xét hình (b) và hình (c):
Ta có M là trung điểm B1B’.
Suy ra \(B'{\rm{ }} = {\rm{ }}{Đ_M}({B_1}).\)
Chứng minh tương tự, ta được \(A'{\rm{ }} = {\rm{ }}{Đ_M}({A_1}).\)
Do đó
Khi đó \({Đ_M}\) biến hình (b) thành hình (c).
Vì vậy phép đồng dạng tỉ số 1 biến hình (b) thành hình (c).
Do đó hình (b) và hình (c) đồng dạng với nhau.
⦁ Ta xét hình (a) và hình (c):
Ta có phép đồng dạng có được bằng cách thực hiện liên tiếp \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) và \({Đ_M}\) biến hình (a) thành hình (c).
Do đó hình (a) và hình (c) đồng dạng với nhau.
Vậy các cặp hình đồng dạng với nhau có trong Hình 5 là: cặp hình (a) và (b); cặp hình (b) và (c); cặp hình (c) và (a).
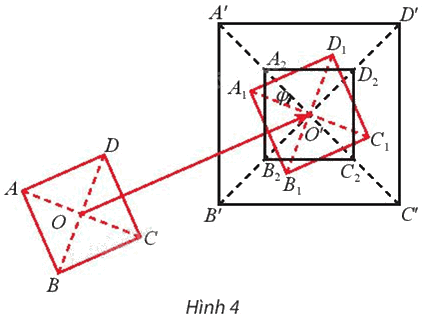
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
a) Gọi \({A_1}{B_1}{C_1}{Đ_1}\) là ảnh của hình vuông ABCD qua phép tịnh tiến theo vectơ . Gọi φ là góc lượng giác (O’A1, O’A’). Tìm ảnh \({A_2}{B_2}{C_2}{Đ_2}\) của hình vuông A1B1C1D1 qua phép quay \({Q_{\left( {O',{\rm{ }}\varphi } \right)}}.\)
b) Cho biết \(\overrightarrow {OA'} = k\overrightarrow {O{A_2}} \). Tìm ảnh của hình vuông \({A_2}{B_2}{C_2}{Đ_2}\) qua phép vị tự \({V_{\left( {O',{\rm{ }}k} \right)}}.\)
c) Từ kết quả của câu a) và b), hãy cho biết ta có thể kết luận là hai hình vuông tùy ý luôn đồng dạng với nhau được không. Giải thích.
Phương pháp giải:
Để tìm ảnh của một hình qua một phép biến hình ta tìm ảnh của các điểm thuộc hình đó qua phép biến hình. Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
a) Do phép quay là phép dời hình nên ảnh A2B2C2D2 của hình vuông A1B1C1D1 cũng là hình vuông có kích thước bằng hình vuông A1B1C1D1.
Theo đề, ta có A1B1C1D1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo \(\overrightarrow {{\rm{OO}}'} \).
Mà O là tâm của hình vuông ABCD.
Nên ta có O’ là tâm của hình vuông A1B1C1D1.
Mà A2B2C2D2 là ảnh của hình vuông A1B1C1D1 qua \({Q_{(O',\;\varphi )}}\;\) (giả thiết).
Suy ra O’ cũng là tâm của hình vuông A2B2C2D2.
Do đó O’A2 = O’B2 = O’C2 = O’D2.
Để tìm ảnh A2B2C2D2 của hình vuông A1B1C1D1 qua ta tìm vị trí các điểm A2, B2, C2, D2 theo thứ tự là ảnh của các điểm A1, B1, C1, D1 qua \({Q_{(O',\;\varphi )}}.\)
Ta có \({A_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({A_1}).\)
Suy ra \(O'{A_2}\; = {\rm{ }}O'{A_1}\;,{\rm{ }}(O'{A_1},{\rm{ }}O'{A_2}){\rm{ }} = {\rm{ }}\varphi .\)
Mà \(\varphi {\rm{ }} = {\rm{ }}(O'{A_1},{\rm{ }}O'A')\) (giả thiết).
Do đó A2 nằm trên đường thẳng O’A’.
Vì vậy A2 là một điểm nằm trên đường thẳng O’A’ thỏa mãn O’A2 = O’A1.
Ta có \({B_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({B_1}).\)
Suy ra \(O'{B_2}\; = {\rm{ }}O'{B_1},(O'{B_1},{\rm{ }}O'{B_2}){\rm{ }} = {\rm{ }}\varphi .\)
Ta có O’ là tâm của hình vuông A2B2C2D2 và hình vuông A’B’C’D’.
Khi đó \(\widehat {{A_1}O'B} = {90^o} - \widehat {{A_2}O'{A_1}}\) và \(\widehat {{A_1}O'B'} = {90^o} - \widehat {A'O'{A_1}}\)
Suy ra \(\widehat {{A_1}O'{B_2}} = \widehat {{A_1}O'B'}\)
Do đó B2 nằm trên đường thẳng O’B’.
Vì vậy B2 là một điểm nằm trên đường thẳng O’B’ thỏa mãn \(O'{B_2}\; = {\rm{ }}O'{B_1}.\)
Chứng minh tương tự, ta được:
⦁ C2 nằm trên đường thẳng O’C’ thỏa mãn O’C2 = O’C1;
⦁ D2 nằm trên đường thẳng O’D’ thỏa mãn O’D2 = O’D1.
Vậy ảnh của hình vuông A1B1C1D1 qua Q(O’, φ) là hình vuông A2B2C2D2 thỏa mãn A2, B2, C2, D2 lần lượt nằm trên O’A’, O’B’, O’C’, O’D’ và O’B2 = O’C2 = O’D2 = O’A2 = O’A1.
b) Để tìm ảnh của hình vuông A2B2C2D2 qua V(O’, k), ta tìm ảnh của các điểm A2, B2, C2, D2 qua V(O’, k).
Theo đề, ta có \(\overrightarrow {O'A'} = k\overrightarrow {O'{A_2}} \) .
Suy ra \({V_{\left( {O',{\rm{ }}k} \right)}}({A_2}){\rm{ }} = {\rm{ }}A',{\rm{ }}O'A'{\rm{ }} = {\rm{ }}\left| k \right|.O'{A_2}.\)
Ta có O’A2 = O’B2 (chứng minh trên) và O’A’ = O’B’ (O’ là tâm của hình vuông A’B’C’D’).
Suy ra \(\frac{{O'{B_2}}}{{O'B'}} = \frac{{O'{A_2}}}{{O'A'}} = \frac{1}{{\left| k \right|}}\)
Do đó O’B’ = |k|.O’B2.
Mà \(\overrightarrow {O'B'} ,\overrightarrow {O'{B_2}} \) cùng phương (B2 là một điểm nằm trên đường thẳng O’B’).
Suy ra \(\overrightarrow {O'B'} = k.\overrightarrow {O'{B_2}} \)
Do đó \({V_{\left( {O',{\rm{ }}k} \right)}}({B_2}){\rm{ }} = {\rm{ }}B'.\)
Chứng minh tương tự, ta được \({V_{\left( {O',{\rm{ }}k} \right)}}({C_2}){\rm{ }} = {\rm{ }}C',{\rm{ }}{V_{\left( {O',{\rm{ }}k} \right)}}({Đ_2}){\rm{ }} = {\rm{ }}D'.\)
Vậy ảnh của hình vuông A2B2C2D2 qua \({V_{\left( {O',{\rm{ }}k} \right)}}\;\) là hình vuông A’B’C’D’.
c) Từ kết quả của câu a) và b), ta thấy phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O’, góc quay φ = (O’A1, O’A’) và phép vị tự tâm O, tỉ số k biến hình vuông ABCD thành hình vuông A’B’C’D’.
Do đó hai hình vuông ABCD và A’B’C’D’ đồng dạng với nhau.
Vậy hai hình vuông tùy ý luôn đồng dạng với nhau.
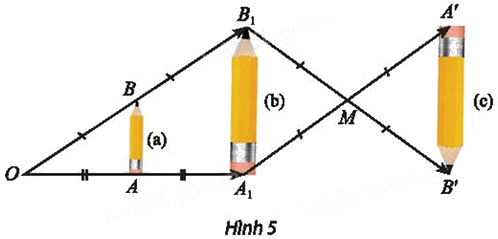
Cho hai hình vuông tùy ý ABCD và A’B’C’D’ có giao điểm hai đường chéo lần lượt là O và O’ (Hình 4).
a) Gọi \({A_1}{B_1}{C_1}{Đ_1}\) là ảnh của hình vuông ABCD qua phép tịnh tiến theo vectơ . Gọi φ là góc lượng giác (O’A1, O’A’). Tìm ảnh \({A_2}{B_2}{C_2}{Đ_2}\) của hình vuông A1B1C1D1 qua phép quay \({Q_{\left( {O',{\rm{ }}\varphi } \right)}}.\)
b) Cho biết \(\overrightarrow {OA'} = k\overrightarrow {O{A_2}} \). Tìm ảnh của hình vuông \({A_2}{B_2}{C_2}{Đ_2}\) qua phép vị tự \({V_{\left( {O',{\rm{ }}k} \right)}}.\)
c) Từ kết quả của câu a) và b), hãy cho biết ta có thể kết luận là hai hình vuông tùy ý luôn đồng dạng với nhau được không. Giải thích.
Phương pháp giải:
Để tìm ảnh của một hình qua một phép biến hình ta tìm ảnh của các điểm thuộc hình đó qua phép biến hình. Sau đó nối chúng lại với nhau.
Lời giải chi tiết:
a) Do phép quay là phép dời hình nên ảnh A2B2C2D2 của hình vuông A1B1C1D1 cũng là hình vuông có kích thước bằng hình vuông A1B1C1D1.
Theo đề, ta có A1B1C1D1 là ảnh của hình vuông ABCD qua phép tịnh tiến theo \(\overrightarrow {{\rm{OO}}'} \).
Mà O là tâm của hình vuông ABCD.
Nên ta có O’ là tâm của hình vuông A1B1C1D1.
Mà A2B2C2D2 là ảnh của hình vuông A1B1C1D1 qua \({Q_{(O',\;\varphi )}}\;\) (giả thiết).
Suy ra O’ cũng là tâm của hình vuông A2B2C2D2.
Do đó O’A2 = O’B2 = O’C2 = O’D2.
Để tìm ảnh A2B2C2D2 của hình vuông A1B1C1D1 qua ta tìm vị trí các điểm A2, B2, C2, D2 theo thứ tự là ảnh của các điểm A1, B1, C1, D1 qua \({Q_{(O',\;\varphi )}}.\)
Ta có \({A_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({A_1}).\)
Suy ra \(O'{A_2}\; = {\rm{ }}O'{A_1}\;,{\rm{ }}(O'{A_1},{\rm{ }}O'{A_2}){\rm{ }} = {\rm{ }}\varphi .\)
Mà \(\varphi {\rm{ }} = {\rm{ }}(O'{A_1},{\rm{ }}O'A')\) (giả thiết).
Do đó A2 nằm trên đường thẳng O’A’.
Vì vậy A2 là một điểm nằm trên đường thẳng O’A’ thỏa mãn O’A2 = O’A1.
Ta có \({B_2}\; = {\rm{ }}{Q_{(O',\;\varphi )}}({B_1}).\)
Suy ra \(O'{B_2}\; = {\rm{ }}O'{B_1},(O'{B_1},{\rm{ }}O'{B_2}){\rm{ }} = {\rm{ }}\varphi .\)
Ta có O’ là tâm của hình vuông A2B2C2D2 và hình vuông A’B’C’D’.
Khi đó \(\widehat {{A_1}O'B} = {90^o} - \widehat {{A_2}O'{A_1}}\) và \(\widehat {{A_1}O'B'} = {90^o} - \widehat {A'O'{A_1}}\)
Suy ra \(\widehat {{A_1}O'{B_2}} = \widehat {{A_1}O'B'}\)
Do đó B2 nằm trên đường thẳng O’B’.
Vì vậy B2 là một điểm nằm trên đường thẳng O’B’ thỏa mãn \(O'{B_2}\; = {\rm{ }}O'{B_1}.\)
Chứng minh tương tự, ta được:
⦁ C2 nằm trên đường thẳng O’C’ thỏa mãn O’C2 = O’C1;
⦁ D2 nằm trên đường thẳng O’D’ thỏa mãn O’D2 = O’D1.
Vậy ảnh của hình vuông A1B1C1D1 qua Q(O’, φ) là hình vuông A2B2C2D2 thỏa mãn A2, B2, C2, D2 lần lượt nằm trên O’A’, O’B’, O’C’, O’D’ và O’B2 = O’C2 = O’D2 = O’A2 = O’A1.
b) Để tìm ảnh của hình vuông A2B2C2D2 qua V(O’, k), ta tìm ảnh của các điểm A2, B2, C2, D2 qua V(O’, k).
Theo đề, ta có \(\overrightarrow {O'A'} = k\overrightarrow {O'{A_2}} \) .
Suy ra \({V_{\left( {O',{\rm{ }}k} \right)}}({A_2}){\rm{ }} = {\rm{ }}A',{\rm{ }}O'A'{\rm{ }} = {\rm{ }}\left| k \right|.O'{A_2}.\)
Ta có O’A2 = O’B2 (chứng minh trên) và O’A’ = O’B’ (O’ là tâm của hình vuông A’B’C’D’).
Suy ra \(\frac{{O'{B_2}}}{{O'B'}} = \frac{{O'{A_2}}}{{O'A'}} = \frac{1}{{\left| k \right|}}\)
Do đó O’B’ = |k|.O’B2.
Mà \(\overrightarrow {O'B'} ,\overrightarrow {O'{B_2}} \) cùng phương (B2 là một điểm nằm trên đường thẳng O’B’).
Suy ra \(\overrightarrow {O'B'} = k.\overrightarrow {O'{B_2}} \)
Do đó \({V_{\left( {O',{\rm{ }}k} \right)}}({B_2}){\rm{ }} = {\rm{ }}B'.\)
Chứng minh tương tự, ta được \({V_{\left( {O',{\rm{ }}k} \right)}}({C_2}){\rm{ }} = {\rm{ }}C',{\rm{ }}{V_{\left( {O',{\rm{ }}k} \right)}}({Đ_2}){\rm{ }} = {\rm{ }}D'.\)
Vậy ảnh của hình vuông A2B2C2D2 qua \({V_{\left( {O',{\rm{ }}k} \right)}}\;\) là hình vuông A’B’C’D’.
c) Từ kết quả của câu a) và b), ta thấy phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O’, góc quay φ = (O’A1, O’A’) và phép vị tự tâm O, tỉ số k biến hình vuông ABCD thành hình vuông A’B’C’D’.
Do đó hai hình vuông ABCD và A’B’C’D’ đồng dạng với nhau.
Vậy hai hình vuông tùy ý luôn đồng dạng với nhau.
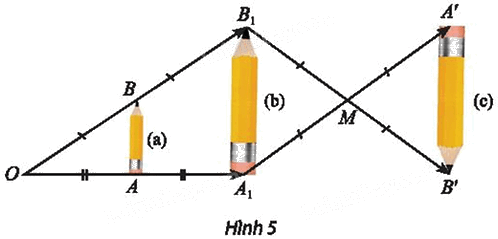
Tìm các cặp hình đồng dạng với nhau có trong Hình 5.
Phương pháp giải:
Quan sát hình 5 để tìm các cặp hình đồng dạng
Lời giải chi tiết:
⦁ Xét cặp hình (a) và (b):
Ta có \(O{A_1}\; = {\rm{ }}2OA\) và \(\overrightarrow {O{A_1}} \;,\,\overrightarrow {OA} \) cùng phương.
Suy ra \(\overrightarrow {O{A_1}} = 2\,\overrightarrow {OA} \)
Do đó \({V_{\left( {O,{\rm{ }}2} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Chứng minh tương tự, ta được \({V_{\left( {O,{\rm{ }}2} \right)}}\left( B \right){\rm{ }} = {\rm{ }}{B_1}.\)
Vì vậy \({V_{\left( {O,{\rm{ }}2} \right)}}\left( {AB} \right){\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Khi đó \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) biến hình (a) thành hình (b).
Vì vậy phép đồng dạng tỉ số 2 biến hình (a) thành hình (b).
Do đó hình (a) và hình (b) đồng dạng với nhau.
⦁ Ta xét hình (b) và hình (c):
Ta có M là trung điểm B1B’.
Suy ra \(B'{\rm{ }} = {\rm{ }}{Đ_M}({B_1}).\)
Chứng minh tương tự, ta được \(A'{\rm{ }} = {\rm{ }}{Đ_M}({A_1}).\)
Do đó
Khi đó \({Đ_M}\) biến hình (b) thành hình (c).
Vì vậy phép đồng dạng tỉ số 1 biến hình (b) thành hình (c).
Do đó hình (b) và hình (c) đồng dạng với nhau.
⦁ Ta xét hình (a) và hình (c):
Ta có phép đồng dạng có được bằng cách thực hiện liên tiếp \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) và \({Đ_M}\) biến hình (a) thành hình (c).
Do đó hình (a) và hình (c) đồng dạng với nhau.
Vậy các cặp hình đồng dạng với nhau có trong Hình 5 là: cặp hình (a) và (b); cặp hình (b) và (c); cặp hình (c) và (a).
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Việc nắm vững kiến thức nền tảng và phương pháp giải là yếu tố then chốt để giải quyết thành công các bài tập trong mục này. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 39 và 40, đồng thời phân tích các phương pháp tiếp cận hiệu quả.
Bài tập 1 thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết một vấn đề cụ thể. Để giải quyết bài tập này, chúng ta cần:
Ví dụ, nếu bài tập yêu cầu tính giá trị của một biểu thức, chúng ta cần xác định đúng thứ tự thực hiện các phép toán và áp dụng các quy tắc về dấu ngoặc.
Bài tập 2 thường mang tính ứng dụng cao, yêu cầu học sinh liên hệ kiến thức đã học với các tình huống thực tế. Để giải quyết bài tập này, chúng ta cần:
Ví dụ, nếu bài tập yêu cầu tính diện tích của một mảnh đất hình chữ nhật, chúng ta cần xác định đúng chiều dài và chiều rộng của mảnh đất và áp dụng công thức tính diện tích.
Bài tập 3 thường có độ khó cao hơn, yêu cầu học sinh vận dụng kiến thức một cách linh hoạt và sáng tạo. Để giải quyết bài tập này, chúng ta cần:
Ví dụ, nếu bài tập yêu cầu chứng minh một đẳng thức, chúng ta cần sử dụng các phép biến đổi đại số để đưa đẳng thức về dạng đơn giản nhất.
Bài tập 1: (Giải thích chi tiết từng bước giải, kèm theo công thức và kết quả).
Bài tập 2: (Giải thích chi tiết từng bước giải, kèm theo công thức và kết quả).
Bài tập 3: (Giải thích chi tiết từng bước giải, kèm theo công thức và kết quả).
Bài tập 1: (Giải thích chi tiết từng bước giải, kèm theo công thức và kết quả).
Bài tập 2: (Giải thích chi tiết từng bước giải, kèm theo công thức và kết quả).
Bài tập 3: (Giải thích chi tiết từng bước giải, kèm theo công thức và kết quả).
Để đạt kết quả tốt nhất khi giải bài tập Toán 11 - Chân trời sáng tạo, các em cần lưu ý:
Hy vọng rằng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải quyết các bài tập trong mục 2 trang 39, 40 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!