Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng.
Trong mặt phẳng tọa độ Oxy, tìm ảnh qua ĐO của
a) điểm M(3; –4);
b) đường thẳng d: x – 3y + 6 = 0;
c) đường tròn (C): (x + 2)2 + (y – 1)2 = 4.
Phương pháp giải:
Nếu \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
a) Gọi M’ là ảnh của M qua ĐO.
Suy ra O là trung điểm của MM’ với \(M\left( {3;{\rm{ }}-4} \right).\)
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_O} - {x_M} = 2.0 - 3 = - 3\\{y_{M'}} = 2{y_O} - {y_M} = 2.0 + 4 = 4\end{array} \right.\)
Vậy \(M'\left( {-3;{\rm{ }}4} \right).\)
b) • Chọn \(A\left( {0;{\rm{ }}2} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0.\)
Gọi A’là ảnh của A qua \({Đ_O}.\)
Suy ra O là trung điểm của AA’ với A(0; 2)
Do đó \(\left\{ \begin{array}{l}{x_{A'}} = 2{x_O} - {x_A} = 2.0 - 0 = 0\\{y_{A'}} = 2{y_O} - {y_A} = 2.0 - 2 = - 2\end{array} \right.\)
Vì vậy A’(0; –2).
• Đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\rm{\vec n}} = \left( {1; - 3} \right)\)
Gọi d’ là ảnh của d qua \({Đ_O}.\)
Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là \({\rm{\vec n}} = \left( {1; - 3} \right)\) làm vectơ pháp tuyến.
Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ \({\rm{\vec n}} = \left( {1; - 3} \right)\) pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x-3y-6 = 0.\)
c) Đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}\; = {\rm{ }}4\) có tâm I(–2; 1), bán kính R = 2.
Gọi (C’) là ảnh của (C) qua ĐO nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2.
Gọi I’= ĐO(I).
Suy ra O là trung điểm \(II'.\)
Do đó \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_O} - {x_I} = 2.0 + 2 = 2\\{y_{I'}} = 2{y_O} - {y_I} = 2.0 - 1 = - 1\end{array} \right.\)
Vì vậy tọa độ I’(2; –1).
Vậy đường tròn (C’) là ảnh của (C) qua ĐO, có tâm I’(2; –1) và R’ = 2 nên có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\)
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua ĐO. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.
Phương pháp giải:
Vẽ hình sau đó quan sát và so sánh
Lời giải chi tiết:

Theo đề, ta có \({Đ_O}\left( A \right){\rm{ }} = {\rm{ }}A'.\)
Suy ra O là trung điểm AA’, do đó \(OA{\rm{ }} = {\rm{ }}OA'.\)
Chứng minh tương tự, ta được \(OB{\rm{ }} = {\rm{ }}OB'.\)
Xét \(\Delta OAB\) và \(\Delta OA'B'\), có:
\(OA{\rm{ }} = {\rm{ }}OA'\) (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (đối đỉnh);
\(OB{\rm{ }} = {\rm{ }}OB'\) (chứng minh trên).
Do đó \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\left( {c.g.c} \right).\)
Suy ra \(A'B'{\rm{ }} = {\rm{ }}AB\) (cặp cạnh tương ứng).
Vậy \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\) và \(A'B'{\rm{ }} = {\rm{ }}AB.\)
Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.
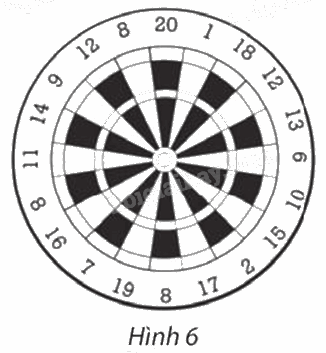
Phương pháp giải:
Quan sát hình 6 để tìm
Lời giải chi tiết:
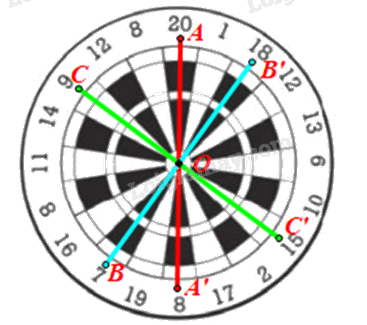
Gọi O là tâm bia.
• Lấy điểm A nằm trong ô có điểm ghi số 20. Lấy A’ đối xứng với A qua O.
Khi đó ta được điểm A’ nằm trong ô có điểm ghi số 8.
• Lấy điểm B nằm trong ô có điểm ghi số 7. Lấy B’ đối xứng với B qua O.
Khi đó ta được điểm B’ nằm trong ô có điểm ghi số 18.
• Lấy điểm C nằm trong ô có điểm ghi số 9. Lấy C’ đối xứng với C qua O.
Khi đó ta được điểm C’ nằm trong ô có điểm ghi số 15.
Vậy điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9 lần lượt là 8; 18; 15.
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua ĐO. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.
Phương pháp giải:
Vẽ hình sau đó quan sát và so sánh
Lời giải chi tiết:
Theo đề, ta có \({Đ_O}\left( A \right){\rm{ }} = {\rm{ }}A'.\)
Suy ra O là trung điểm AA’, do đó \(OA{\rm{ }} = {\rm{ }}OA'.\)
Chứng minh tương tự, ta được \(OB{\rm{ }} = {\rm{ }}OB'.\)
Xét \(\Delta OAB\) và \(\Delta OA'B'\), có:
\(OA{\rm{ }} = {\rm{ }}OA'\) (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (đối đỉnh);
\(OB{\rm{ }} = {\rm{ }}OB'\) (chứng minh trên).
Do đó \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\left( {c.g.c} \right).\)
Suy ra \(A'B'{\rm{ }} = {\rm{ }}AB\) (cặp cạnh tương ứng).
Vậy \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\) và \(A'B'{\rm{ }} = {\rm{ }}AB.\)
Trong mặt phẳng tọa độ Oxy, tìm ảnh qua ĐO của
a) điểm M(3; –4);
b) đường thẳng d: x – 3y + 6 = 0;
c) đường tròn (C): (x + 2)2 + (y – 1)2 = 4.
Phương pháp giải:
Nếu \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
a) Gọi M’ là ảnh của M qua ĐO.
Suy ra O là trung điểm của MM’ với \(M\left( {3;{\rm{ }}-4} \right).\)
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_O} - {x_M} = 2.0 - 3 = - 3\\{y_{M'}} = 2{y_O} - {y_M} = 2.0 + 4 = 4\end{array} \right.\)
Vậy \(M'\left( {-3;{\rm{ }}4} \right).\)
b) • Chọn \(A\left( {0;{\rm{ }}2} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0.\)
Gọi A’là ảnh của A qua \({Đ_O}.\)
Suy ra O là trung điểm của AA’ với A(0; 2)
Do đó \(\left\{ \begin{array}{l}{x_{A'}} = 2{x_O} - {x_A} = 2.0 - 0 = 0\\{y_{A'}} = 2{y_O} - {y_A} = 2.0 - 2 = - 2\end{array} \right.\)
Vì vậy A’(0; –2).
• Đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\rm{\vec n}} = \left( {1; - 3} \right)\)
Gọi d’ là ảnh của d qua \({Đ_O}.\)
Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là \({\rm{\vec n}} = \left( {1; - 3} \right)\) làm vectơ pháp tuyến.
Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ \({\rm{\vec n}} = \left( {1; - 3} \right)\) pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x-3y-6 = 0.\)
c) Đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}\; = {\rm{ }}4\) có tâm I(–2; 1), bán kính R = 2.
Gọi (C’) là ảnh của (C) qua ĐO nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2.
Gọi I’= ĐO(I).
Suy ra O là trung điểm \(II'.\)
Do đó \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_O} - {x_I} = 2.0 + 2 = 2\\{y_{I'}} = 2{y_O} - {y_I} = 2.0 - 1 = - 1\end{array} \right.\)
Vì vậy tọa độ I’(2; –1).
Vậy đường tròn (C’) là ảnh của (C) qua ĐO, có tâm I’(2; –1) và R’ = 2 nên có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\)
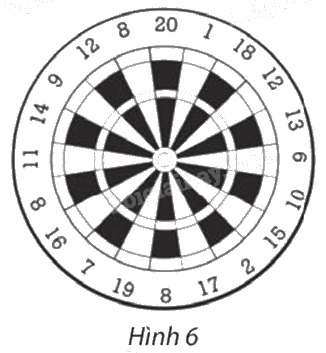
Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.
Phương pháp giải:
Quan sát hình 6 để tìm
Lời giải chi tiết:
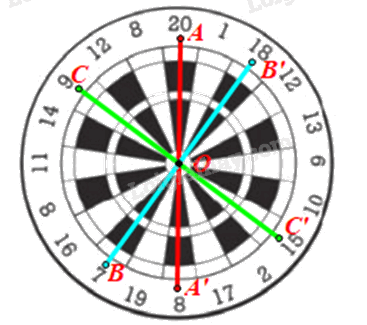
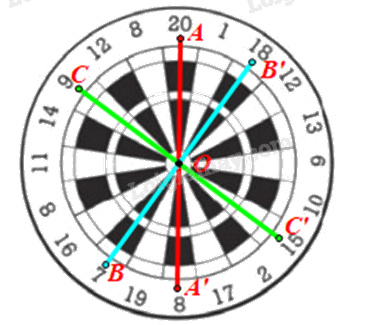
Gọi O là tâm bia.
• Lấy điểm A nằm trong ô có điểm ghi số 20. Lấy A’ đối xứng với A qua O.
Khi đó ta được điểm A’ nằm trong ô có điểm ghi số 8.
• Lấy điểm B nằm trong ô có điểm ghi số 7. Lấy B’ đối xứng với B qua O.
Khi đó ta được điểm B’ nằm trong ô có điểm ghi số 18.
• Lấy điểm C nằm trong ô có điểm ghi số 9. Lấy C’ đối xứng với C qua O.
Khi đó ta được điểm C’ nằm trong ô có điểm ghi số 15.
Vậy điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9 lần lượt là 8; 18; 15.
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 11, là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là rất cần thiết để giải quyết các bài toán thực tế và đạt kết quả tốt trong các kỳ thi.
Mục 2 bao gồm các nội dung chính sau:
Trang 21 tập trung vào các bài tập vận dụng định nghĩa đạo hàm và ý nghĩa hình học của đạo hàm. Các bài tập này yêu cầu học sinh phải hiểu rõ khái niệm đạo hàm và biết cách tính đạo hàm của các hàm số đơn giản.
Bài 1: Tính đạo hàm của hàm số f(x) = x2 tại x = 2.
Lời giải:
f'(x) = limh→0 (f(x+h) - f(x)) / h = limh→0 ((x+h)2 - x2) / h = limh→0 (2xh + h2) / h = limh→0 (2x + h) = 2x.
Vậy, f'(2) = 2 * 2 = 4.
Trang 22 tập trung vào các bài tập vận dụng các quy tắc tính đạo hàm. Các bài tập này yêu cầu học sinh phải nắm vững các quy tắc tính đạo hàm và biết cách áp dụng chúng để tính đạo hàm của các hàm số phức tạp hơn.
Bài 2: Tính đạo hàm của hàm số f(x) = sin(x) + cos(x).
Lời giải:
f'(x) = d/dx (sin(x)) + d/dx (cos(x)) = cos(x) - sin(x).
Để học tốt môn Toán 11 - Chân trời sáng tạo, các em nên:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng rằng lời giải chi tiết bài tập mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạo tại giaitoan.edu.vn sẽ giúp các em học sinh hiểu sâu sắc hơn về kiến thức đạo hàm và tự tin giải quyết các bài toán liên quan. Chúc các em học tập tốt!