Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Giải bài 8 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúng tôi cam kết hỗ trợ bạn học toán hiệu quả và đạt kết quả tốt nhất.
Bài viết này sẽ cung cấp đầy đủ các bước giải, phân tích và giải thích rõ ràng để bạn có thể nắm vững kiến thức và tự tin giải các bài tập tương tự.
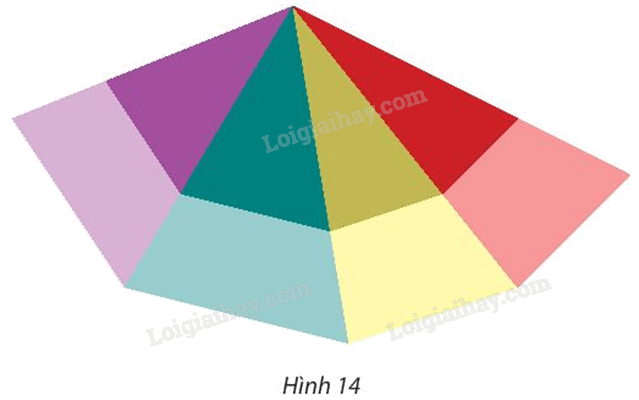
Trong Hình 14, tìm phép vị tự được dùng để biến bốn tam giác nhỏ thành bốn tam giác lớn.
Đề bài
Trong Hình 14, tìm phép vị tự được dùng để biến bốn tam giác nhỏ thành bốn tam giác lớn.
Phương pháp giải - Xem chi tiết
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết
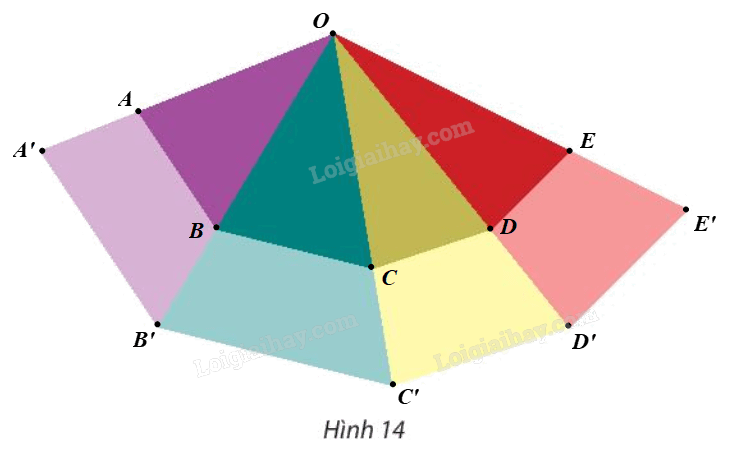
Giả sử ta chọn điểm O như hình vẽ.
Ta đặt bốn tam giác nhỏ là \(\Delta OAB,{\rm{ }}\Delta OBC,{\rm{ }}\Delta OCD\;\) và \(\Delta \)ODE và bốn tam giác lớn là OA’B’, \(\Delta \)OB’C’, \(\Delta \)OC’D’ và \(\Delta \)OD’E’ (hình vẽ).
Yêu cầu bài toán đưa về tìm phép vị tự biến \(\Delta OAB,{\rm{ }}\Delta OBC,{\rm{ }}\Delta OCD\;\) và \(\Delta \)ODE lần lượt thành \(\Delta \)OA’B’, \(\Delta \)OB’C’, \(\Delta \)OC’D’ và \(\Delta \)OD’E’.
Tức là ta đi tìm phép vị tự biến các điểm O, A, B, C, D, E lần lượt thành O, A’, B’, C’, D’, E’.
Ta thấy O là giao điểm của các đường thẳng AA’, BB’, CC’, DD’, EE’.
Ta chứng minh các điểm O, A’, B’, C’, D’, E’ lần lượt là ảnh của các điểm O, A, B, C, D, E qua \({V_{\left( {O,{\rm{ }}k} \right)}}.\)
Thật vậy, ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right){\rm{ }} = {\rm{ }}A'.\)
Suy ra \(\overrightarrow {O{A'}} = k\overrightarrow {OA} \) và \(OA'{\rm{ }} = {\rm{ }}\left| k \right|.OA.\)
Vì A, A’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0\).
Do đó \(k = \frac{{OA'}}{{OA}}\)
Mà \(k = \frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\) nên \(\overrightarrow {OB'} = k\overrightarrow {OB} \) do đó \({V_{\left( {O,{\rm{ }}k} \right)}}\left( B \right){\rm{ }} = {\rm{ }}B'.\)
Tương tự như trên ta chứng minh được \({V_{\left( {O,{\rm{ }}k} \right)}}\left( C \right){\rm{ }} = {\rm{ }}C',{\rm{ }}{V_{\left( {O,{\rm{ }}k} \right)}}\left( D \right){\rm{ }} = {\rm{ }}D',{\rm{ }}{V_{\left( {O,{\rm{ }}k} \right)}}\left( E \right){\rm{ }} = {\rm{ }}E'.\)
Vậy \({V_{\left( {O,\frac{{OA'}}{{OA}}} \right)}}\) là phép vị tự cần tìm.
Bài 8 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 8 trang 36, chúng tôi sẽ cung cấp lời giải chi tiết cho từng phần của bài tập. Dưới đây là ví dụ về lời giải cho một phần của bài tập:
Lời giải:
Để tính đạo hàm của hàm số y = sin(x^2 + 1), ta sử dụng quy tắc tính đạo hàm của hàm hợp:
y' = cos(x^2 + 1) * (x^2 + 1)' = cos(x^2 + 1) * 2x = 2x * cos(x^2 + 1)
Khi giải bài 8 trang 36, bạn cần lưu ý những điều sau:
Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:
Bài 8 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin giải quyết bài tập này và đạt kết quả tốt nhất.
| Dạng bài | Phương pháp giải |
|---|---|
| Tính đạo hàm | Sử dụng quy tắc tính đạo hàm, quy tắc hàm hợp |
| Tìm đạo hàm cấp hai | Tính đạo hàm bậc nhất, sau đó tính đạo hàm của đạo hàm bậc nhất |
| Ứng dụng đạo hàm | Tìm cực trị, khoảng đơn điệu, giải bài toán thực tế |