Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong Chuyên đề học tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Ở mục 1 này, chúng ta sẽ cùng nhau giải quyết các bài tập trang 70, 71 và 72, tập trung vào các khái niệm và kỹ năng quan trọng được trình bày trong chương trình học.
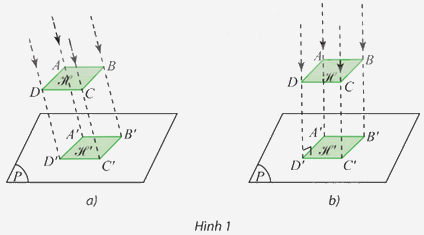
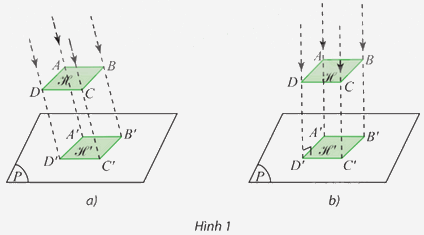
Hình 1 thể hiện hai cách chiếu hình ℋ thành hình ℋ ’ lên mặt phẳng (P).
Hình 1 thể hiện hai cách chiếu hình ℋ thành hình ℋ ’ lên mặt phẳng (P). Mô tả cách vẽ các đỉnh của hình chiếu ℋ ’ trong mỗi trường hợp.
Phương pháp giải:
Quan sát hình 1 để trả lời
Lời giải chi tiết:
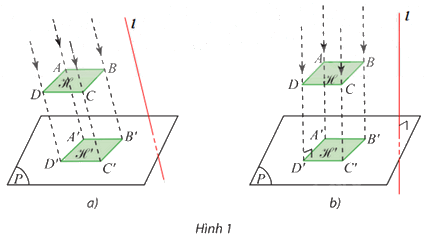
⦁ Hình 1a:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ cắt (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
⦁ Hình 1b:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ vuông góc với (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
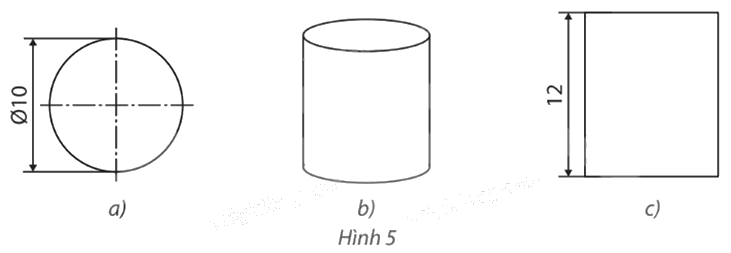
Dưới đây là ba hình biểu diễn của hình trụ có độ dài đường kính đáy bằng 10 cm và chiều cao bằng 12 cm. Chỉ ra phép chiếu được sử dụng tương ứng với mỗi hình.
Phương pháp giải:
Quan sát hình 5 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 5a là hình tròn có độ dài đường kính đáy bằng 10 cm nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với mặt đáy của hình trụ.
– Phép chiếu được sử dụng ở Hình 5b là phép chiếu song song.
– Hình 5c là hình chữ nhật có chiều dài bằng 12 cm (bằng chiều cao của hình trụ) nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với đường sinh của hình trụ.
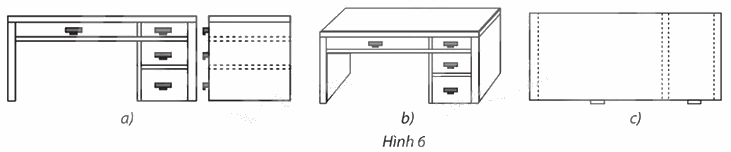
Phép chiếu nào được sử dụng để vẽ các hình biểu diễn của bàn làm việc trong Hình 6?
Phương pháp giải:
Quan sát hình 6 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 6a:
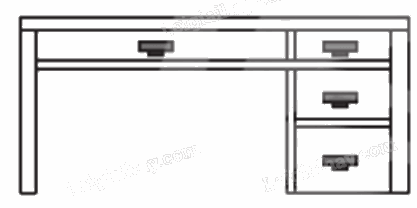
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt trước của bàn làm việc.
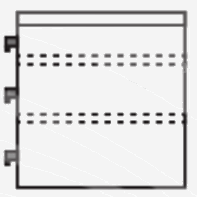
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bên của bàn làm việc.
– Hình 6b:
Phép chiếu được sử dụng ở Hình 6b là phép chiếu song song.
– Hình 6c:
Phép chiếu được sử dụng ở Hình 6c là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bàn của bàn làm việc.
Hình 1 thể hiện hai cách chiếu hình ℋ thành hình ℋ ’ lên mặt phẳng (P). Mô tả cách vẽ các đỉnh của hình chiếu ℋ ’ trong mỗi trường hợp.
Phương pháp giải:
Quan sát hình 1 để trả lời
Lời giải chi tiết:
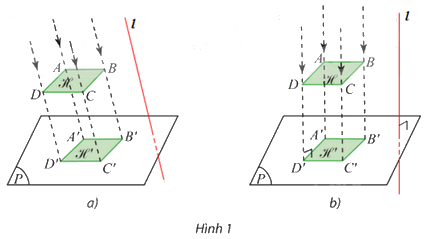
⦁ Hình 1a:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ cắt (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
⦁ Hình 1b:
Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ vuông góc với (P) (hình vẽ).
Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.
Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.
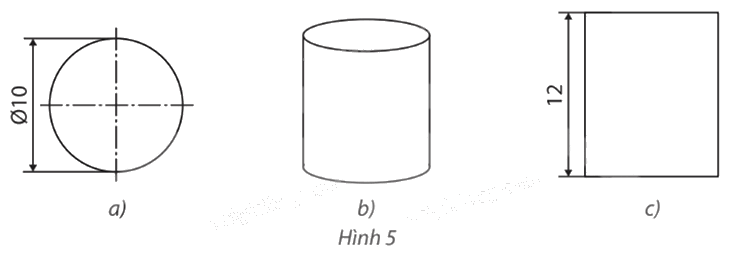
Dưới đây là ba hình biểu diễn của hình trụ có độ dài đường kính đáy bằng 10 cm và chiều cao bằng 12 cm. Chỉ ra phép chiếu được sử dụng tương ứng với mỗi hình.
Phương pháp giải:
Quan sát hình 5 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 5a là hình tròn có độ dài đường kính đáy bằng 10 cm nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với mặt đáy của hình trụ.
– Phép chiếu được sử dụng ở Hình 5b là phép chiếu song song.
– Hình 5c là hình chữ nhật có chiều dài bằng 12 cm (bằng chiều cao của hình trụ) nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với đường sinh của hình trụ.
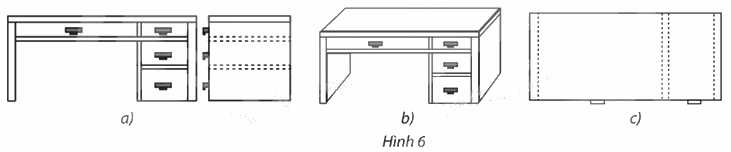
Phép chiếu nào được sử dụng để vẽ các hình biểu diễn của bàn làm việc trong Hình 6?
Phương pháp giải:
Quan sát hình 6 và dựa vào kiến thức
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\)tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết:
– Hình 6a:
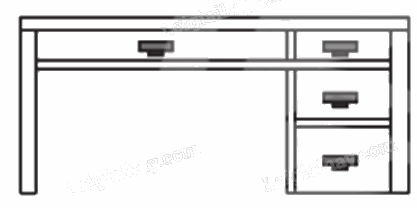
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt trước của bàn làm việc.
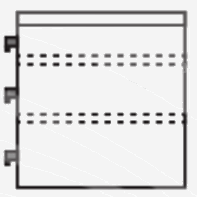
Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bên của bàn làm việc.
– Hình 6b:
Phép chiếu được sử dụng ở Hình 6b là phép chiếu song song.
– Hình 6c:
Phép chiếu được sử dụng ở Hình 6c là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bàn của bàn làm việc.
Chuyên đề học tập Toán 11 - Chân trời sáng tạo là một tài liệu quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Mục 1 của chuyên đề này thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học.
Trước khi đi vào giải bài tập, chúng ta cần xác định rõ nội dung chính của Mục 1. Thông thường, mục này sẽ giới thiệu một khái niệm mới, một định lý quan trọng hoặc một phương pháp giải toán đặc biệt. Việc hiểu rõ nội dung này là điều kiện tiên quyết để giải quyết các bài tập một cách hiệu quả.
Trang 70 thường chứa các bài tập áp dụng trực tiếp các kiến thức đã học trong phần lý thuyết. Các bài tập này thường có dạng trắc nghiệm hoặc tự luận đơn giản, giúp học sinh làm quen với cách sử dụng các công thức và định lý. Dưới đây là giải chi tiết một số bài tập tiêu biểu:
Trang 71 thường chứa các bài tập phức tạp hơn, đòi hỏi học sinh phải kết hợp nhiều kiến thức và kỹ năng khác nhau. Các bài tập này thường có dạng tự luận, yêu cầu học sinh trình bày lời giải một cách rõ ràng, logic.
Trang 72 thường chứa các bài tập nâng cao, đòi hỏi học sinh phải có khả năng tư duy sáng tạo và vận dụng linh hoạt các kiến thức đã học. Các bài tập này thường có dạng mở, yêu cầu học sinh tự tìm tòi, khám phá các phương pháp giải khác nhau.
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Giải chi tiết) |
| Bài 2 | (Giải chi tiết) |
| Bài 3 | (Giải chi tiết) |
Để giải bài tập một cách hiệu quả, các em cần lưu ý một số điều sau:
Luyện tập thường xuyên là yếu tố then chốt để nắm vững kiến thức và rèn luyện kỹ năng giải toán. Các em nên dành thời gian giải các bài tập trong sách giáo khoa, sách bài tập và các đề thi thử để làm quen với các dạng bài khác nhau và nâng cao khả năng giải quyết vấn đề.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trang 70, 71, 72 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!