Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 18 trang 42, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả tốt nhất.
Cho tam giác ABC có góc B, góc C đều là góc nhọn.
Đề bài
Cho tam giác ABC có góc B, góc C đều là góc nhọn. Nêu cách vẽ hình chữ nhật DEFG có đỉnh D, đỉnh E thuộc cạnh BC, đỉnh F, đỉnh G thuộc cạnh AC, AB và có EF = 2DE.
Phương pháp giải - Xem chi tiết
Dựa vào phép vị tự để làm: Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết
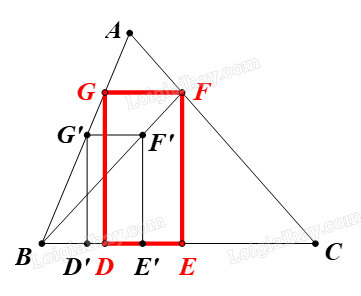
⦁ Phân tích:
Lấy điểm G’ bất kì trên AB.
Dựng hình chữ nhật D’E’F’G’ có \(\;E'F'{\rm{ }} = {\rm{ }}2D'E'\) và hai đỉnh D’, E’ thuộc BC.
Đường thẳng BF’ cắt AC tại F.
Do D’E’F’G’ là hình chữ nhật nên \(G'D'{\rm{ }} \bot {\rm{ }}D'E'\) hay \(G'D'{\rm{ }} \bot {\rm{ }}BC.\)
Mà GD ⊥ BC (do DEFG là hình chữ nhật).
Nên G’D’ // GD.
Chứng minh tương tự, ta được E’F’ // EF.
Vì D’E’F’G’ là hình chữ nhật nên G’F’ // D’E’ hay G’F’ // BC.
Mà GF // BC (do DEFG là hình chữ nhật).
Suy ra GF // G’F’.
Áp dụng định lí Thales, ta được \(\frac{{BG}}{{BG'}} = \frac{{BF}}{{BF'}}\)
Suy ra \(BF' = \frac{{BG'}}{{BG}}.BF\)
Mà \(\overrightarrow {BF'} ,\overrightarrow {BF} \) cùng hướng.
Do đó \(\overrightarrow {BF'} = \frac{{BG'}}{{BG}}.\overrightarrow {BF} \)
Vì vậy \({\rm{F'}} = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( F \right)\,\,(1)\)
Chứng minh tương tự, ta được \(D' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( D \right)\) và \(E' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( E \right)\,\,(2)\)
Lại có \(G' = {V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\left( G \right)\,\,(3)\)
Từ (1), (2), (3), ta thu được \({V_{\left( {B,\frac{{BG'}}{{BG}}} \right)}}\) biến hình chữ nhật D’E’F’G’ thành hình chữ nhật DEFG. Từ đó, ta suy ra cách dựng hình chữ nhật DEFG.
⦁ Cách dựng:
Lấy điểm G’ tùy ý trên AB.
Dựng hình chữ nhật D’E’F’G’ có E’F’ = 2D’E’, hai đỉnh D’, E’ nằm trên BC.
Đường thẳng BF’ cắt AC tại F.
Đường thẳng qua F song song với BC cắt AB tại G.
Gọi D, E lần lượt là hình chiếu của G, F lên BC.
Vậy ta đã dựng xong hình chữ nhật DEFG.
Bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 18 trang 42 thường yêu cầu học sinh:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 18. Tuy nhiên, dựa trên cấu trúc chung của Chuyên đề học tập Toán 11 Chân trời sáng tạo, chúng ta có thể đưa ra một ví dụ minh họa về cách giải một bài toán tương tự:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Hãy tìm cực trị của hàm số.
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 18 trang 42 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải bài tập. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.