Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho tập hợp số V = {1; 2; 3; 4; 5; 6; 7}. Hãy vẽ đồ thị G có các đỉnh biểu diễn các phần tử của V
Đề bài
Cho tập hợp số V = {1; 2; 3; 4; 5; 6; 7}. Hãy vẽ đồ thị G có các đỉnh biểu diễn các phần tử của V, hai đỉnh biểu diễn hai số m và n kề nhau nếu m + n là bội của 3.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đồ thị:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết
Trong tập hợp số V, các cặp số là bội của 3 là:
• (1 và 2); (1 và 5);
• (2 và 4); (2 và 7);
• (3 và 6);
• (4 và 5);
• (5 và 7).
Ta vẽ đồ thị G có 7 đỉnh \({A_1};{\rm{ }}{A_2};{\rm{ }}{A_3};{\rm{ }}{A_4};{\rm{ }}{A_5};{\rm{ }}{A_6};{\rm{ }}{A_7}\;\) biểu diễn bảy số trong tập hợp số V.
Hai đỉnh biểu diễn hai số m và n được nối bằng một cạnh nếu m + n là bội của 3.
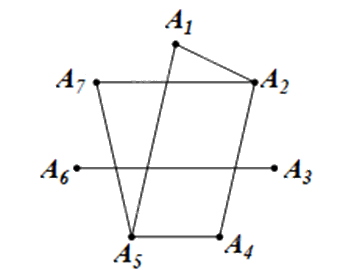
Ta có đồ thị G như sau:
Bài 6 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 6 trang 67, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập.
Lời giải:
f'(x) = 3x2 - 6x + 2
Lời giải:
g'(x) = 4x3 - 8x
Giải phương trình g'(x) = 0, ta được x = 0, x = √2, x = -√2
Lập bảng biến thiên, ta thấy hàm số đạt cực đại tại x = -√2 và x = √2, đạt cực tiểu tại x = 0.
Để giải các bài tập về đạo hàm một cách hiệu quả, các em cần:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Khi giải bài tập đạo hàm, các em cần lưu ý:
Bài 6 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn khi giải các bài tập tương tự.
| Dạng bài | Phương pháp giải |
|---|---|
| Tính đạo hàm | Sử dụng quy tắc tính đạo hàm |
| Tìm cực trị | Giải phương trình đạo hàm bằng 0, lập bảng biến thiên |
| Khảo sát hàm số | Tính đạo hàm, tìm cực trị, xét giới hạn |