Bài 5 trang 59 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, cập nhật và phù hợp với chương trình học Toán 11 hiện hành.
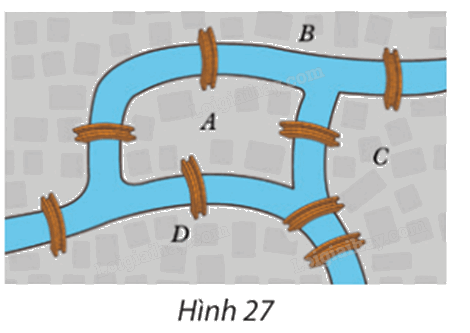
Có bốn khu phố A, B, C và D được nối với nhau bằng những cây cầu như Hình 27.
Đề bài
Có bốn khu phố A, B, C và D được nối với nhau bằng những cây cầu như Hình 27. Có hay không cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát? Nếu có, hãy chỉ ra một cách đi như vậy.
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ, dựa vào kiến thức:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải chi tiết
Biểu thị mỗi khu phố bằng một đỉnh, mỗi cây cầu bằng một cạnh nối hai đỉnh, ta được đồ thị như hình vẽ.

Ta có d(A) = d(B) = d(C) = d(D) = 4.
Suy ra tất cả các đỉnh của đồ thị trên đều có bậc chẵn.
Do đó đồ thị trên có chu trình Euler.
Vậy nói cách khác, có cách đi qua tất cả các cây cầu, mỗi cây cầu chỉ qua một lần, rồi quay trở lại nơi xuất phát.
Chẳng hạn, bắt đầu từ đỉnh A, ta có thể đi theo chu trình Euler: AabADcdDBCA
Bài 5 trang 59 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, bao gồm đạo hàm của hàm số, đạo hàm tại một điểm, và các quy tắc tính đạo hàm. Ngoài ra, việc hiểu rõ mối liên hệ giữa đạo hàm và tính đơn điệu của hàm số cũng rất quan trọng.
Trước khi bắt đầu giải bài, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu tìm đạo hàm của hàm số, xác định các điểm cực trị, hoặc khảo sát sự biến thiên của hàm số. Việc xác định đúng yêu cầu của bài toán sẽ giúp học sinh lựa chọn phương pháp giải phù hợp và tránh sai sót.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét cụ thể nội dung của bài toán. Giả sử bài toán yêu cầu tìm đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1.
Sử dụng quy tắc đạo hàm của tổng và hiệu, ta có:
f'(x) = (x3)' - (3x2)' + (2x)' - (1)'
f'(x) = 3x2 - 6x + 2
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x + 2 = 0
Sử dụng công thức nghiệm của phương trình bậc hai, ta có:
x = (6 ± √(36 - 4*3*2)) / (2*3) = (6 ± √12) / 6 = (6 ± 2√3) / 6 = 1 ± √3/3
Vậy, x1 = 1 + √3/3 và x2 = 1 - √3/3 là các điểm cực trị.
Ta xét dấu của f''(x) tại các điểm cực trị:
f''(x) = (3x2 - 6x + 2)' = 6x - 6
f''(x1) = 6(1 + √3/3) - 6 = 2√3 > 0, vậy x1 là điểm cực tiểu.
f''(x2) = 6(1 - √3/3) - 6 = -2√3 < 0, vậy x2 là điểm cực đại.
Hàm số f(x) có điểm cực đại tại x2 = 1 - √3/3 và điểm cực tiểu tại x1 = 1 + √3/3.
Đạo hàm không chỉ được sử dụng để tìm các điểm cực trị mà còn có nhiều ứng dụng quan trọng khác trong việc khảo sát hàm số. Ví dụ, đạo hàm có thể được sử dụng để xác định khoảng đồng biến, khoảng nghịch biến của hàm số, tìm giới hạn của hàm số tại vô cùng, và vẽ đồ thị hàm số. Việc nắm vững các ứng dụng này sẽ giúp học sinh hiểu sâu sắc hơn về tính chất của hàm số và có thể giải quyết các bài toán phức tạp hơn.
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự với các hàm số khác nhau. Ví dụ, hãy tìm đạo hàm, các điểm cực trị và khảo sát sự biến thiên của hàm số g(x) = x4 - 4x2 + 3.
Bài 5 trang 59 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các khái niệm cơ bản, phân tích đề bài một cách cẩn thận, và áp dụng các phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài toán này và các bài toán tương tự.