Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 4 trang 14, giúp bạn nắm vững kiến thức và kỹ năng giải toán.

Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.

Cho hai điểm B, C cố định trên đường tròn \(\left( {O;{\rm{ }}R} \right)\) và một điểm A thay đổi trên đường tròn đó

Đề bài

Cho hai điểm B, C cố định trên đường tròn \(\left( {O;{\rm{ }}R} \right)\) và một điểm A thay đổi trên đường tròn đó. Chứng minh trực tâm H của tam giác ABC luôn nằm trên một đường tròn cố định.

Phương pháp giải - Xem chi tiết Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo 1

Ta đi chứng minh trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn \(\left( {O;{\rm{ }}R} \right)\) qua phép tịnh tiến theo \(\overrightarrow {B'C} \)

Lời giải chi tiết

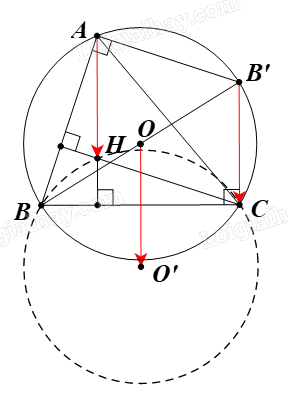
Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo 2

Kẻ đường kính BB’.

Do B, C cố định trên (O) nên B’, C cũng cố định trên (O).

Suy ra \(\overrightarrow {B'C} \) là vectơ không đổi.

Ta có \(\widehat {BCB'} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O)).

Suy ra \(BC \bot B'C.\)

Mà \(AH \bot BC\) (do H là trực tâm của ∆ABC).

Do đó \(AH//B'C\,\,\left( 1 \right)\)

Chứng minh tương tự, ta được \(AB'//CH{\rm{ }}\left( 2 \right)\)

Từ (1), (2), suy ra tứ giác AHCB’ là hình bình hành.

Suy ra \(AH{\rm{ }} = {\rm{ }}B'C.\)

Mà \(AH{\rm{ }}//{\rm{ }}B'C\) (chứng minh trên).

Vì vậy \(\overrightarrow {AH} = \overrightarrow {B'C} \)

Do đó \(H = {T_{\overrightarrow {B'C} }}\left( A \right)\).

Vậy khi A thay đổi trên đường tròn (O) thì trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn (O) là đường tròn (O’) qua \({{\rm{T}}_{\overrightarrow {B'C} }}\).

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo – hành trang không thể thiếu trong chuyên mục Bài tập Toán lớp 11 trên nền tảng toán học. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo: Tổng quan

Bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích, suy luận và áp dụng các công thức, định lý đã học để tìm ra đáp án chính xác.

Nội dung bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Bài 4 thường bao gồm các dạng bài tập sau:

Xác định tập xác định của hàm số: Yêu cầu học sinh tìm ra các giá trị của x mà hàm số có nghĩa.
Tìm tập giá trị của hàm số: Yêu cầu học sinh xác định khoảng giá trị mà hàm số có thể đạt được.
Xét tính đơn điệu của hàm số: Yêu cầu học sinh xác định hàm số đồng biến hay nghịch biến trên một khoảng nào đó.
Tìm cực trị của hàm số: Yêu cầu học sinh tìm ra các điểm cực đại, cực tiểu của hàm số.
Vẽ đồ thị hàm số: Yêu cầu học sinh vẽ đồ thị của hàm số dựa trên các thông tin đã tìm được.

Phương pháp giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Để giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:

Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài toán và các thông tin đã cho.
Xác định kiến thức cần sử dụng: Xác định các công thức, định lý, quy tắc liên quan đến bài toán.
Lập kế hoạch giải: Xác định các bước cần thực hiện để giải bài toán.
Thực hiện giải bài: Thực hiện các bước đã lập kế hoạch một cách cẩn thận và chính xác.
Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác và hợp lý.

Ví dụ minh họa giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Bài toán: Cho hàm số y = x² - 4x + 3. Tìm tập xác định, tập giá trị, cực trị và vẽ đồ thị của hàm số.

Lời giải:

Tập xác định: Hàm số y = x² - 4x + 3 là một hàm đa thức, do đó tập xác định của hàm số là R.
Tập giá trị: Hàm số y = x² - 4x + 3 có dạng parabol với hệ số a = 1 > 0, do đó tập giá trị của hàm số là [-1, +∞).
Cực trị: Hàm số y = x² - 4x + 3 có đỉnh tại điểm (2, -1), do đó hàm số có cực tiểu tại x = 2 và giá trị cực tiểu là -1.
Đồ thị: Đồ thị của hàm số y = x² - 4x + 3 là một parabol có đỉnh tại điểm (2, -1) và cắt trục hoành tại các điểm (1, 0) và (3, 0).

Lưu ý khi giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Khi giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo, bạn cần lưu ý những điều sau:

Nắm vững kiến thức cơ bản: Đảm bảo rằng bạn đã nắm vững các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng giải toán.
Sử dụng các công cụ hỗ trợ: Sử dụng máy tính bỏ túi, phần mềm vẽ đồ thị để hỗ trợ quá trình giải bài.
Tham khảo các nguồn tài liệu: Tham khảo sách giáo khoa, sách bài tập, các trang web học toán online để tìm hiểu thêm về các kiến thức và phương pháp giải bài.

Kết luận

Bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức và kỹ năng giải toán. Hy vọng rằng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!