Bài 6 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về dãy số, cấp số cộng, cấp số nhân để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13).
Đề bài
Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao cho MN vuông góc với a, b và tổng khoảng cách AM + NB ngắn nhất.
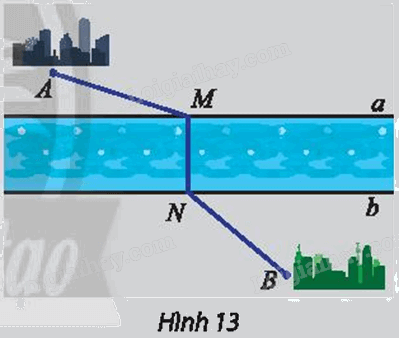
Phương pháp giải - Xem chi tiết
Ta đi chứng minh tổng khoảng cách \(AM{\rm{ }} + {\rm{ }}NB\) ngắn nhất khi và chỉ khi \(A'N{\rm{ }} + {\rm{ }}NB'{\rm{ }} = {\rm{ }}A'B'.\) Với A’, B’ là ảnh của A, B qua \({Đ_d}\) (d là đường trung trực của đoạn MN)
Lời giải chi tiết
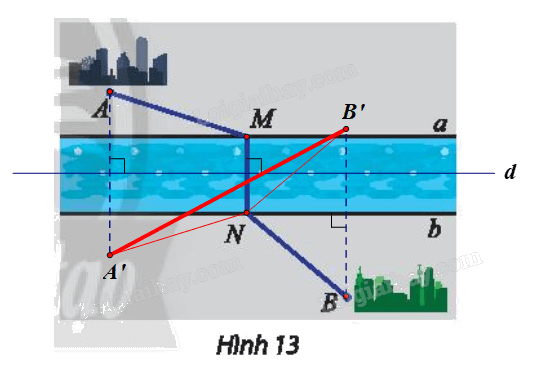
Gọi d là đường trung trực của đoạn MN.
Suy ra điểm N là ảnh của điểm M qua \({Đ_d}\)
Lấy điểm A’ là ảnh của điểm A qua \({Đ_d}\)
Suy ra đoạn A’N là ảnh của đoạn AM qua \({Đ_d}\)
Do đó \(A'N{\rm{ }} = {\rm{ }}AM.\)
Lấy điểm B’ là ảnh của điểm B qua
Suy ra b là đường trung trực của đoạn BB’.
Mà \(N \in b\) (giả thiết).
Do đó \(NB'{\rm{ }} = {\rm{ }}NB.\)
Ta có \(AM{\rm{ }} + {\rm{ }}NB{\rm{ }} = {\rm{ }}A'N{\rm{ }} + {\rm{ }}NB'.\)
Áp dụng bất đẳng thức tam giác cho ∆A’NB’, ta được: \(A'N{\rm{ }} + {\rm{ }}NB'{\rm{ }} \ge {\rm{ }}A'B'.\)
Do đó tổng khoảng cách \(AM{\rm{ }} + {\rm{ }}NB\) ngắn nhất khi và chỉ khi \(A'N{\rm{ }} + {\rm{ }}NB'{\rm{ }} = {\rm{ }}A'B'.\)
Tức là, ba điểm A’, N, B’ thẳng hàng.
Vậy N là giao điểm của A’B’ và bờ b, M là điểm nằm bên bờ a thỏa mãn M = Đd(N), với d là đường trung trực của đoạn MN, \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right),{\rm{ }}B'{\rm{ }} = {\rm{ }}{Đ_b}\left( B \right).\)
Bài 6 trang 19 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng các kiến thức về dãy số, đặc biệt là cấp số cộng và cấp số nhân, vào các bài toán thực tế. Mục tiêu chính của bài tập này là giúp học sinh rèn luyện kỹ năng phân tích, suy luận logic và khả năng giải quyết vấn đề.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài 6 trang 19 sẽ đưa ra một tình huống thực tế liên quan đến dãy số, chẳng hạn như sự tăng trưởng dân số, sự phân rã của một chất phóng xạ, hoặc các bài toán về lãi kép. Dựa vào đó, học sinh cần xác định được loại dãy số phù hợp và áp dụng công thức tương ứng để tìm ra kết quả.
Để giải quyết bài 6 trang 19 một cách hiệu quả, học sinh cần nắm vững các công thức sau:
Dưới đây là hướng dẫn giải chi tiết bài 6 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Lưu ý rằng, tùy thuộc vào từng dạng bài cụ thể, cách giải có thể khác nhau. Tuy nhiên, các bước cơ bản thường bao gồm:
Ví dụ: Một công ty dự kiến tăng lương cho nhân viên hàng năm là 5%. Nếu lương khởi điểm của một nhân viên là 8 triệu đồng, hãy tính lương của nhân viên đó sau 5 năm làm việc.
Giải:
Đây là một bài toán về cấp số nhân, với:
Lương sau 5 năm làm việc là:
u5 = u1 * q(5-1) = 8 * (1.05)4 ≈ 9.66 triệu đồng
Để củng cố kiến thức và kỹ năng giải bài tập về dãy số, bạn có thể luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Hãy chú trọng vào việc phân tích đề bài, xác định đúng loại dãy số và áp dụng công thức một cách chính xác.
Trong quá trình học tập và giải bài tập, đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên, bạn bè hoặc các nguồn tài liệu trực tuyến. Việc trao đổi, thảo luận và học hỏi lẫn nhau sẽ giúp bạn hiểu sâu hơn về kiến thức và nâng cao khả năng giải quyết vấn đề.
Bài 6 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng ứng dụng kiến thức về dãy số vào thực tế. Bằng cách nắm vững các công thức, phân tích đề bài một cách kỹ lưỡng và luyện tập thường xuyên, bạn sẽ tự tin giải quyết mọi bài toán về dãy số.