Bài 4 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 80, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài tập.
Vẽ hình chiếu vuông góc của các hình sau:
Đề bài
Vẽ hình chiếu vuông góc của các hình sau:
a) Hình hộp chữ nhật có ba kích thước 2 cm; 4 cm; 6 cm.
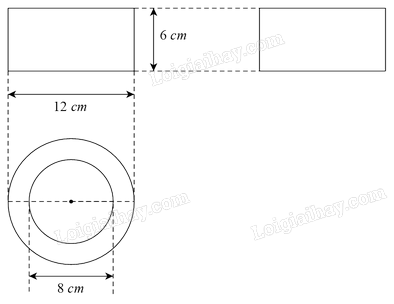
b) Hình trụ rỗng tròn xoay có chiều cao 6 cm và bán kính đáy ngoài 6 cm, bán kính đáy trong 4 cm.
Phương pháp giải - Xem chi tiết
- Trong không gian, cho mặt phẳng \(\left( P \right)\)và đường thẳng \(l\) cắt \(\left( P \right)\). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt \(\left( P \right)\) tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng \(\left( P \right)\) được gọi là phép chiếu song song lên mặt phẳng \(\left( P \right)\) theo phương \(l\).
- Nếu phương chiếu vuông góc với mặt phẳng chiếu \(\left( P \right)\) thì phép chiếu song song được gọi là phép chiếu vuông góc lên mặt phẳng \(\left( P \right)\)
Lời giải chi tiết
a) Hình chiếu vuông góc của hình hộp chữ nhật có ba kích thước 2 cm; 4 cm; 6 cm là:

b) Hình trụ rỗng tròn xoay có bán kính đáy ngoài 6 cm và bán kính đáy trong 4 cm.
Suy ra hình trụ rỗng tròn xoay có đường kính ngoài 12 cm và đường kính trong 8 cm.
Hình chiếu vuông góc của hình trụ rỗng tròn xoay có chiều cao 6 cm và bán kính đáy ngoài 6 cm, bán kính đáy trong 4 cm là:
Bài 4 trang 80 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến sự biến thiên của hàm số. Cụ thể, bài toán yêu cầu học sinh xác định khoảng đơn điệu của hàm số, tìm cực trị và vẽ đồ thị hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý về đạo hàm, bao gồm đạo hàm của hàm số, điều kiện cần và đủ để hàm số đơn điệu, điều kiện để hàm số đạt cực trị.
Trước khi bắt đầu giải bài toán, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu và các dữ kiện đã cho. Sau đó, học sinh cần xác định phương pháp giải phù hợp. Trong trường hợp bài 4 trang 80, phương pháp giải chính là sử dụng đạo hàm để xét sự biến thiên của hàm số. Cụ thể, các bước giải như sau:
Để minh họa phương pháp giải, chúng ta sẽ cùng nhau giải bài 4 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo. (Giả sử đề bài cụ thể là: Xét hàm số f(x) = x^3 - 3x^2 + 2. Tìm khoảng đơn điệu và cực trị của hàm số.)
f'(x) = 3x^2 - 6x
f'(x) = 0 ⇔ 3x^2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, các điểm dừng là x = 0 và x = 2.
Xét dấu f'(x):
f''(x) = 6x - 6
f''(0) = -6 < 0 ⇒ Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2
f''(2) = 6 > 0 ⇒ Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2
(Phần này yêu cầu mô tả cách vẽ đồ thị dựa trên các thông tin đã tìm được, bao gồm các điểm cực trị, khoảng đơn điệu và giao điểm với các trục tọa độ. Việc vẽ đồ thị có thể được thực hiện bằng phần mềm hoặc thủ công.)
Việc giải bài 4 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo không chỉ giúp học sinh củng cố kiến thức về đạo hàm mà còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau, như kinh tế, kỹ thuật, vật lý,... Ví dụ, trong kinh tế, đạo hàm được sử dụng để tính toán chi phí biên, doanh thu biên và lợi nhuận biên. Trong kỹ thuật, đạo hàm được sử dụng để tính toán vận tốc, gia tốc và các đại lượng liên quan đến chuyển động.
Bài 4 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và sự biến thiên của hàm số. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.