Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Chuyên đề học tập. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 48 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
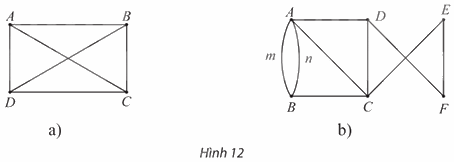
Hãy chỉ ra các đỉnh, các cạnh, số đỉnh, số cạnh của mỗi đồ thị như Hình 12.
Đề bài
Hãy chỉ ra các đỉnh, các cạnh, số đỉnh, số cạnh của mỗi đồ thị như Hình 12.
Phương pháp giải - Xem chi tiết
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết
⦁ Hình 12a:
Các đỉnh của đồ thị là: A, B, C, D.Số đỉnh của đồ thị là: 4.
Các cạnh của đồ thị là: AB, AC, AD, BC, BD, CD.Số cạnh của đồ thị là: 6.
⦁ Hình 12b:
Các đỉnh của đồ thị là: A, B, C, D, E, F.Số đỉnh của đồ thị là: 6.
Các cạnh của đồ thị là: m, n, AC, AD, BC, CD, CE, DF, EF.Số cạnh của đồ thị là: 9.
Bài 1 trang 48 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, và cách vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 1 trang 48 thường yêu cầu chúng ta:
Để giải bài 1 trang 48, chúng ta sẽ thực hiện các bước sau:
Giả sử hàm số được cho là y = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước trên để giải bài tập:
Bước 1: Tập xác định của hàm số là R.
Bước 2: Đạo hàm của hàm số là y' = 3x2 - 6x.
Bước 3: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2. Vậy hàm số có hai điểm cực trị là x = 0 và x = 2.
Bước 4: Vẽ đồ thị hàm số dựa trên các thông tin đã tính toán.
Bước 5: Nghiên cứu sự biến thiên của hàm số, ta thấy hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2).
Khi giải bài tập về hàm số và đồ thị, bạn cần lưu ý những điều sau:
Bài 1 trang 48 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số và đồ thị. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Tập xác định | Tập hợp các giá trị của x sao cho hàm số có nghĩa. |
| Đạo hàm | Tốc độ thay đổi của hàm số. |
| Điểm cực trị | Điểm mà tại đó đạo hàm bằng 0 hoặc không tồn tại. |