Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 2 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo, trang 46, 47 và 48. Bài viết này cung cấp phương pháp giải bài tập rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật lời giải các bài tập mới nhất, đảm bảo tính chính xác và hữu ích cho quá trình học tập của bạn.
Đồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng)
Có hay không một đồ thị có ba đỉnh, trong đó hai đỉnh có bậc bằng 2 và một đỉnh có bậc bằng 3?
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Không có, vì tổng tất cả các bậc của các đỉnh là 2 + 2 + 3 = 7 là một số lẻ.
Cho đồ thị như Hình 11.
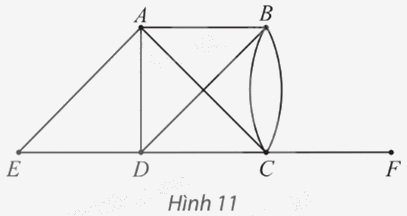
a) Hãy chỉ ra bậc của tất cả các đỉnh và tìm tổng của chúng.
b) Tìm tất cả các đỉnh kề với đỉnh B. Số đỉnh này có bằng bậc của đỉnh B không?
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là d(A)
Lời giải chi tiết:
a) Số cạnh của đồ thị có A là đầu mút là: 4.Suy ra bậc của đỉnh A là: d(A) = 4.
Tương tự như vậy, ta có: d(B) = 4; d(C) = 5; d(D) = 4; d(E) = 2; d(F) = 1.
Tổng các bậc của các đỉnh của đồ thị là: 4 + 4 + 5 + 4 + 2 + 1 = 20.
b) Tất cả các đỉnh kề với đỉnh B là: A, C, D.Suy ra có 3 đỉnh kề với đỉnh B.
Mà bậc của đỉnh B là: d(B) = 4.
Vì 3 ≠ 4 nên 3 ≠ d(B).
Vậy số đỉnh kề với đỉnh B không bằng bậc của đỉnh B.
Đồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng). Biết rằng mỗi con đường ra, vào làng đều phải đi qua một cổng chào; hai con đường khác nhau thì ra, vào làng qua hai cổng chào khác nhau. Ngoài ra, các ngôi làng không còn cổng chào nào khác.
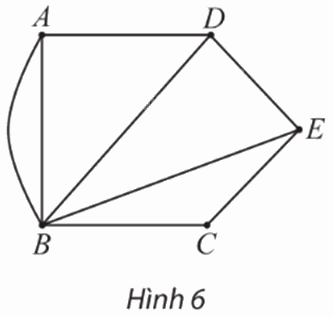
a) Ngôi làng nào có ít cổng chào nhất? Ngôi làng nào có nhiều cổng chào nhất?
b) Năm ngôi làng có tất cả bao nhiêu cổng chào?
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
a) Do ta có 3 con đường để ra, vào ngôi làng A nên ngôi làng A có 3 cổng chào.
Tương tự như vậy, ta có:
⦁ Ngôi làng B có 5 cổng chào;
⦁ Ngôi làng C có 2 cổng chào;
⦁ Ngôi làng D có 3 cổng chào;
⦁ Ngôi làng E có 3 cổng chào.
Vậy ngôi làng có ít cổng chào nhất là ngôi làng C (với 2 cổng chào); ngôi làng có nhiều cổng chào nhất là ngôi làng B (với 5 cổng chào).
b) Quan sát Hình 6, đồ thị có tất cả 8 cạnh (mỗi cạnh biểu diễn 1 con đường giữa hai ngôi làng) nên năm ngôi làng có tất cả 8 cổng chào.
Đồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng). Biết rằng mỗi con đường ra, vào làng đều phải đi qua một cổng chào; hai con đường khác nhau thì ra, vào làng qua hai cổng chào khác nhau. Ngoài ra, các ngôi làng không còn cổng chào nào khác.
a) Ngôi làng nào có ít cổng chào nhất? Ngôi làng nào có nhiều cổng chào nhất?
b) Năm ngôi làng có tất cả bao nhiêu cổng chào?
Phương pháp giải:
Quan sát hình 6 để trả lời
Lời giải chi tiết:
a) Do ta có 3 con đường để ra, vào ngôi làng A nên ngôi làng A có 3 cổng chào.
Tương tự như vậy, ta có:
⦁ Ngôi làng B có 5 cổng chào;
⦁ Ngôi làng C có 2 cổng chào;
⦁ Ngôi làng D có 3 cổng chào;
⦁ Ngôi làng E có 3 cổng chào.
Vậy ngôi làng có ít cổng chào nhất là ngôi làng C (với 2 cổng chào); ngôi làng có nhiều cổng chào nhất là ngôi làng B (với 5 cổng chào).
b) Quan sát Hình 6, đồ thị có tất cả 8 cạnh (mỗi cạnh biểu diễn 1 con đường giữa hai ngôi làng) nên năm ngôi làng có tất cả 8 cổng chào.
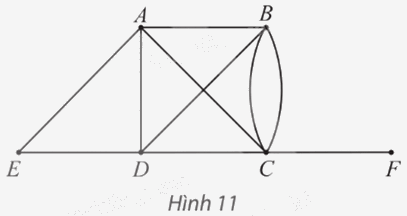
Cho đồ thị như Hình 11.
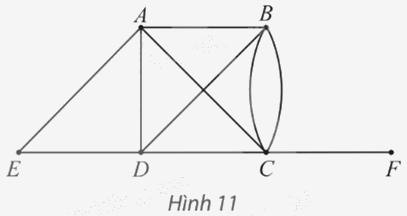
a) Hãy chỉ ra bậc của tất cả các đỉnh và tìm tổng của chúng.
b) Tìm tất cả các đỉnh kề với đỉnh B. Số đỉnh này có bằng bậc của đỉnh B không?
Phương pháp giải:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là d(A)
Lời giải chi tiết:
a) Số cạnh của đồ thị có A là đầu mút là: 4.Suy ra bậc của đỉnh A là: d(A) = 4.
Tương tự như vậy, ta có: d(B) = 4; d(C) = 5; d(D) = 4; d(E) = 2; d(F) = 1.
Tổng các bậc của các đỉnh của đồ thị là: 4 + 4 + 5 + 4 + 2 + 1 = 20.
b) Tất cả các đỉnh kề với đỉnh B là: A, C, D.Suy ra có 3 đỉnh kề với đỉnh B.
Mà bậc của đỉnh B là: d(B) = 4.
Vì 3 ≠ 4 nên 3 ≠ d(B).
Vậy số đỉnh kề với đỉnh B không bằng bậc của đỉnh B.
Có hay không một đồ thị có ba đỉnh, trong đó hai đỉnh có bậc bằng 2 và một đỉnh có bậc bằng 3?
Phương pháp giải:
Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị
Lời giải chi tiết:
Không có, vì tổng tất cả các bậc của các đỉnh là 2 + 2 + 3 = 7 là một số lẻ.
Bài 2 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo, trang 46, 47 và 48, thường tập trung vào việc vận dụng các kiến thức đã học trong chương để giải quyết các bài toán thực tế hoặc chứng minh các định lý. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, các định lý quan trọng và các kỹ năng giải toán cần thiết.
Bài 2 thường được chia thành nhiều phần nhỏ, mỗi phần yêu cầu học sinh áp dụng một kiến thức hoặc kỹ năng khác nhau. Việc phân tích kỹ đề bài và xác định rõ yêu cầu của từng phần là rất quan trọng để đưa ra phương pháp giải phù hợp.
Phần này có thể yêu cầu học sinh tính toán một giá trị cụ thể, chứng minh một đẳng thức hoặc giải một phương trình. Để giải quyết phần này, học sinh cần áp dụng các công thức, định lý và kỹ năng tính toán đã học.
Phần này có thể yêu cầu học sinh giải một bài toán hình học, chứng minh một tính chất hoặc tìm một điểm đặc biệt. Để giải quyết phần này, học sinh cần sử dụng các kiến thức về hình học, các định lý và các kỹ năng vẽ hình.
Phần này có thể yêu cầu học sinh giải một bài toán ứng dụng, phân tích một tình huống thực tế hoặc đưa ra một kết luận dựa trên các dữ kiện đã cho. Để giải quyết phần này, học sinh cần sử dụng các kiến thức về toán học, các kỹ năng phân tích và các kỹ năng tư duy logic.
Giả sử bài 2a yêu cầu tính giá trị của biểu thức A = sin2x + cos2x. Để giải bài này, học sinh cần nhớ lại công thức lượng giác cơ bản sin2x + cos2x = 1. Do đó, A = 1.
Giải bài 2 trang 46, 47, 48 Chuyên đề học tập Toán 11 Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức, kỹ năng và có phương pháp giải bài tập hiệu quả. Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin giải quyết bài toán này một cách thành công.
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| tan x = sin x / cos x | Công thức tính tan x |
| cot x = cos x / sin x | Công thức tính cot x |