Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 17, 18 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
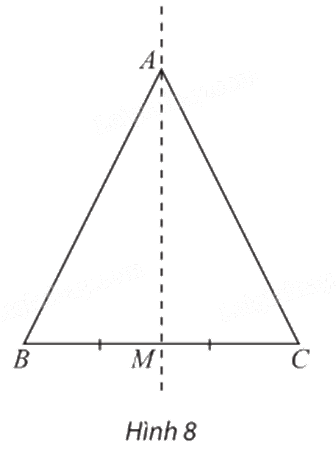
Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC qua phép đối xứng trục AM.
Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC qua phép đối xứng trục AM.
Phương pháp giải:
Để tìm ảnh của tam giác ABC qua phép đối xứng trục AM ta đi tìm ảnh của từng điểm A, B, C qua phép đối xứng trục AM.
Lời giải chi tiết:
Do \(A \in AM\) nên \({Đ_{AM}}\left( A \right){\rm{ }} = {\rm{ }}A.\)
Ta có tam giác ABC cân tại A có AM là đường trung tuyến.
Suy ra AM cũng là đường trung trực của tam giác ABC.
Do đó AM là đường trung trực của đoạn thẳng BC.
Vì vậy \({Đ_{AM}}\left( B \right){\rm{ }} = {\rm{ }}C,{\rm{ }}{Đ_{AM}}\left( C \right){\rm{ }} = {\rm{ }}B.\)
Vậy ảnh của tam giác ABC qua phép đối xứng trục AM là tam giác ACB.
Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.
Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:

Gọi H là giao điểm của AD và BC.
Ta có \(\widehat {ADC} = \widehat {BCD}\) (do ABCD là hình thang cân).
Suy ra tam giác HCD cân tại H.
Do đó \(HD{\rm{ }} = {\rm{ }}HC\).
Vì vậy \(HD{\rm{ }}-{\rm{ }}AD{\rm{ }} = {\rm{ }}HC{\rm{ }}-{\rm{ }}BC\) (AD = BC vì ABCD là hình thang cân có hai đáy AB, CD).
Suy ra \(HA{\rm{ }} = {\rm{ }}HB.\)
Do đó tam giác HAB cân tại H.
Gọi M, N lần lượt là trung điểm của AB và CD.
Tam giác HCD cân tại H có HN là đường trung tuyến.
Suy ra HN cũng là đường cao của tam giác HCD, do đó HN ⊥ CD.
Chứng minh tương tự, ta được HM ⊥ AB.
Mà AB // CD (chứng minh trên).
Suy ra \(HM \bot CD\)
Lại có \(HN \bot CD\) (chứng minh trên).
Do đó ba điểm H, M, N thẳng hàng.
Ta có M là trung điểm AB và \(MN \bot AB\) (chứng minh trên).
Suy ra MN là đường trung trực của hai đoạn thẳng AB.
Khi đó \(B{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( A \right),{\rm{ }}A{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( B \right).\)
Chứng minh tương tự, ta được \(D{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( C \right),{\rm{ }}C{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( D \right).\)
Do đó ảnh của hình thang cân ABCD qua là chính nó.
Vậy trục đối xứng cần tìm là đường thẳng MN, với M, N lần lượt là trung điểm của AB và CD.
Tìm trục đối xứng trong các hình ở Hình 10.

Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
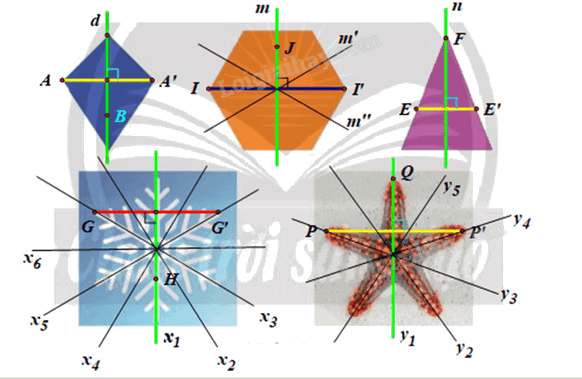
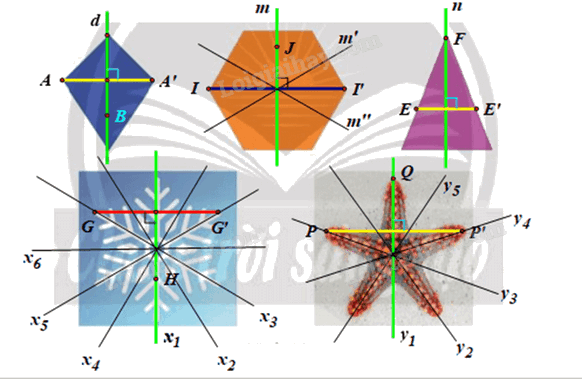
+ Ta xét hình tứ giác:
Chọn đường thẳng d như hình vẽ.
Lấy điểm A nằm trên hình tứ giác nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên hình tứ giác ban đầu.
Lấy điểm B nằm trên hình tứ giác và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tứ giác, ta cũng xác định được ảnh của các điểm đó qua Đd trên hình tứ giác ban đầu.
Do đó Đd biến hình tứ giác đã cho thành chính nó.
Vậy đường thẳng d như hình vẽ là trục đối xứng của hình tứ giác đã cho.
+ Ta xét hình lục giác:
Chọn đường thẳng m là đường trung trực của hai cạnh đối như hình vẽ.
Lấy điểm I nằm trên hình lục giác nhưng không nằm trên đường thẳng m.
Ta đặt \(I'{\rm{ }} = {\rm{ }}{Đ_m}\left( I \right).\)
Khi đó I’ nằm trên hình lục giác ban đầu.
Lấy điểm J nằm trên hình lục giác và nằm trên đường thẳng m.
Ta thấy \(J{\rm{ }} = {\rm{ }}{Đ_m}\left( J \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình lục giác, ta cũng xác định được ảnh của các điểm đó qua Đm trên hình lục giác ban đầu.
Do đó \({Đ_m}\;\) biến hình lục giác đã cho thành chính nó.
Vậy đường thẳng m như hình vẽ là trục đối xứng của hình lục giác đã cho.
Chú ý: Hình lục giác đều có 3 trục đối xứng \(\left( {m,{\rm{ }}m',{\rm{ }}m''} \right).\)
+ Ta xét hình tam giác cân:
Chọn đường thẳng n là đường trung trục của cạnh đáy như hình vẽ.
Lấy điểm E nằm trên hình tam giác nhưng không nằm trên đường thẳng n.
Ta đặt \(E'{\rm{ }} = {\rm{ }}{Đ_n}\left( E \right).\)
Khi đó E’ nằm trên hình tam giác ban đầu.
Lấy điểm F nằm trên hình tam giác và nằm trên đường thẳng n.
Ta thấy \(F{\rm{ }} = {\rm{ }}{Đ_n}\left( F \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tam giác, ta cũng xác định được ảnh của các điểm đó qua Đn trên hình tam giác ban đầu.
Do đó \({Đ_n}\;\) biến hình tam giác đã cho thành chính nó.
Vậy đường thẳng n là trục đối xứng của hình tam giác đã cho.
+ Ta xét hình bông tuyết:
Chọn đường thẳng \({x_1}\;\) như hình vẽ.
Lấy điểm G nằm trên hình bông tuyết nhưng không nằm trên đường thẳng \({x_1}\;\).
Ta đặt \(G' = {Đ_{{x_1}}}\left( G \right)\)
Khi đó G’ nằm trên hình bông tuyết ban đầu.
Lấy điểm H nằm trên hình bông tuyết và nằm trên đường thẳng x1.
Ta thấy \(H = {Đ_{{x_1}}}\left( H \right)\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình bông tuyết, ta cũng xác định được ảnh của các điểm đó qua trên hình bông tuyết ban đầu.
Do đó \({Đ_{{x_1}}}\) biến hình bông tuyết đã cho thành chính nó.
Vậy đường thẳng \({x_1}\) như hình vẽ là trục đối xứng của hình bông tuyết đã cho.
Chú ý: Hình bông tuyết này có 6 trục đối xứng \(({x_1},{\rm{ }}{x_2},{\rm{ }}{x_3},{\rm{ }}{x_4},{\rm{ }}{x_5},{\rm{ }}{x_6}).\)
+ Ta xét hình con sao biển:
Chọn đường thẳng y1 như hình vẽ.
Lấy điểm P nằm trên hình con sao biển nhưng không nằm trên đường thẳng y1.
Ta đặt \(P' = {Đ_{{y_1}}}\left( P \right)\)
Khi đó P’ nằm trên hình con sao biển ban đầu.
Lấy điểm Q nằm trên hình con sao biển và nằm trên đường thẳng y.
Ta thấy \(Q = {Đ_{{y_1}}}\left( Q \right)\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình con sao biển, ta cũng xác định được ảnh của các điểm đó qua \({Đ_{{y_1}}}\) trên hình con sao biển ban đầu.
Do đó \({Đ_{{y_1}}}\) biến hình con sao biển đã cho thành chính nó.
Vậy đường thẳng \({y_1}\) như hình vẽ là trục đối xứng của hình con sao biển đã cho.
Chú ý: Hình con sao biển có 5 trục đối xứng \(({y_1},{\rm{ }}{y_2},{\rm{ }}{y_3},{\rm{ }}{y_4},{\rm{ }}{y_5}).\)
Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC qua phép đối xứng trục AM.

Phương pháp giải:
Để tìm ảnh của tam giác ABC qua phép đối xứng trục AM ta đi tìm ảnh của từng điểm A, B, C qua phép đối xứng trục AM.
Lời giải chi tiết:
Do \(A \in AM\) nên \({Đ_{AM}}\left( A \right){\rm{ }} = {\rm{ }}A.\)
Ta có tam giác ABC cân tại A có AM là đường trung tuyến.
Suy ra AM cũng là đường trung trực của tam giác ABC.
Do đó AM là đường trung trực của đoạn thẳng BC.
Vì vậy \({Đ_{AM}}\left( B \right){\rm{ }} = {\rm{ }}C,{\rm{ }}{Đ_{AM}}\left( C \right){\rm{ }} = {\rm{ }}B.\)
Vậy ảnh của tam giác ABC qua phép đối xứng trục AM là tam giác ACB.
Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.
Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
Gọi H là giao điểm của AD và BC.
Ta có \(\widehat {ADC} = \widehat {BCD}\) (do ABCD là hình thang cân).
Suy ra tam giác HCD cân tại H.
Do đó \(HD{\rm{ }} = {\rm{ }}HC\).
Vì vậy \(HD{\rm{ }}-{\rm{ }}AD{\rm{ }} = {\rm{ }}HC{\rm{ }}-{\rm{ }}BC\) (AD = BC vì ABCD là hình thang cân có hai đáy AB, CD).
Suy ra \(HA{\rm{ }} = {\rm{ }}HB.\)
Do đó tam giác HAB cân tại H.
Gọi M, N lần lượt là trung điểm của AB và CD.
Tam giác HCD cân tại H có HN là đường trung tuyến.
Suy ra HN cũng là đường cao của tam giác HCD, do đó HN ⊥ CD.
Chứng minh tương tự, ta được HM ⊥ AB.
Mà AB // CD (chứng minh trên).
Suy ra \(HM \bot CD\)
Lại có \(HN \bot CD\) (chứng minh trên).
Do đó ba điểm H, M, N thẳng hàng.
Ta có M là trung điểm AB và \(MN \bot AB\) (chứng minh trên).
Suy ra MN là đường trung trực của hai đoạn thẳng AB.
Khi đó \(B{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( A \right),{\rm{ }}A{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( B \right).\)
Chứng minh tương tự, ta được \(D{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( C \right),{\rm{ }}C{\rm{ }} = {\rm{ }}{Đ_{MN}}\left( D \right).\)
Do đó ảnh của hình thang cân ABCD qua là chính nó.
Vậy trục đối xứng cần tìm là đường thẳng MN, với M, N lần lượt là trung điểm của AB và CD.
Tìm trục đối xứng trong các hình ở Hình 10.

Phương pháp giải:
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết:
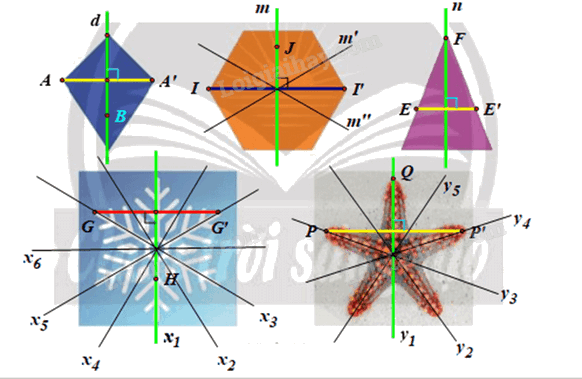
+ Ta xét hình tứ giác:
Chọn đường thẳng d như hình vẽ.
Lấy điểm A nằm trên hình tứ giác nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên hình tứ giác ban đầu.
Lấy điểm B nằm trên hình tứ giác và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tứ giác, ta cũng xác định được ảnh của các điểm đó qua Đd trên hình tứ giác ban đầu.
Do đó Đd biến hình tứ giác đã cho thành chính nó.
Vậy đường thẳng d như hình vẽ là trục đối xứng của hình tứ giác đã cho.
+ Ta xét hình lục giác:
Chọn đường thẳng m là đường trung trực của hai cạnh đối như hình vẽ.
Lấy điểm I nằm trên hình lục giác nhưng không nằm trên đường thẳng m.
Ta đặt \(I'{\rm{ }} = {\rm{ }}{Đ_m}\left( I \right).\)
Khi đó I’ nằm trên hình lục giác ban đầu.
Lấy điểm J nằm trên hình lục giác và nằm trên đường thẳng m.
Ta thấy \(J{\rm{ }} = {\rm{ }}{Đ_m}\left( J \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình lục giác, ta cũng xác định được ảnh của các điểm đó qua Đm trên hình lục giác ban đầu.
Do đó \({Đ_m}\;\) biến hình lục giác đã cho thành chính nó.
Vậy đường thẳng m như hình vẽ là trục đối xứng của hình lục giác đã cho.
Chú ý: Hình lục giác đều có 3 trục đối xứng \(\left( {m,{\rm{ }}m',{\rm{ }}m''} \right).\)
+ Ta xét hình tam giác cân:
Chọn đường thẳng n là đường trung trục của cạnh đáy như hình vẽ.
Lấy điểm E nằm trên hình tam giác nhưng không nằm trên đường thẳng n.
Ta đặt \(E'{\rm{ }} = {\rm{ }}{Đ_n}\left( E \right).\)
Khi đó E’ nằm trên hình tam giác ban đầu.
Lấy điểm F nằm trên hình tam giác và nằm trên đường thẳng n.
Ta thấy \(F{\rm{ }} = {\rm{ }}{Đ_n}\left( F \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình tam giác, ta cũng xác định được ảnh của các điểm đó qua Đn trên hình tam giác ban đầu.
Do đó \({Đ_n}\;\) biến hình tam giác đã cho thành chính nó.
Vậy đường thẳng n là trục đối xứng của hình tam giác đã cho.
+ Ta xét hình bông tuyết:
Chọn đường thẳng \({x_1}\;\) như hình vẽ.
Lấy điểm G nằm trên hình bông tuyết nhưng không nằm trên đường thẳng \({x_1}\;\).
Ta đặt \(G' = {Đ_{{x_1}}}\left( G \right)\)
Khi đó G’ nằm trên hình bông tuyết ban đầu.
Lấy điểm H nằm trên hình bông tuyết và nằm trên đường thẳng x1.
Ta thấy \(H = {Đ_{{x_1}}}\left( H \right)\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình bông tuyết, ta cũng xác định được ảnh của các điểm đó qua trên hình bông tuyết ban đầu.
Do đó \({Đ_{{x_1}}}\) biến hình bông tuyết đã cho thành chính nó.
Vậy đường thẳng \({x_1}\) như hình vẽ là trục đối xứng của hình bông tuyết đã cho.
Chú ý: Hình bông tuyết này có 6 trục đối xứng \(({x_1},{\rm{ }}{x_2},{\rm{ }}{x_3},{\rm{ }}{x_4},{\rm{ }}{x_5},{\rm{ }}{x_6}).\)
+ Ta xét hình con sao biển:
Chọn đường thẳng y1 như hình vẽ.
Lấy điểm P nằm trên hình con sao biển nhưng không nằm trên đường thẳng y1.
Ta đặt \(P' = {Đ_{{y_1}}}\left( P \right)\)
Khi đó P’ nằm trên hình con sao biển ban đầu.
Lấy điểm Q nằm trên hình con sao biển và nằm trên đường thẳng y.
Ta thấy \(Q = {Đ_{{y_1}}}\left( Q \right)\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình con sao biển, ta cũng xác định được ảnh của các điểm đó qua \({Đ_{{y_1}}}\) trên hình con sao biển ban đầu.
Do đó \({Đ_{{y_1}}}\) biến hình con sao biển đã cho thành chính nó.
Vậy đường thẳng \({y_1}\) như hình vẽ là trục đối xứng của hình con sao biển đã cho.
Chú ý: Hình con sao biển có 5 trục đối xứng \(({y_1},{\rm{ }}{y_2},{\rm{ }}{y_3},{\rm{ }}{y_4},{\rm{ }}{y_5}).\)
Mục 3 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập. Việc giải đúng và hiểu rõ các bài tập trong mục này là nền tảng quan trọng để tiếp thu kiến thức ở các phần sau của chương trình.
Để hiểu rõ hơn về nội dung mục 3 trang 17, 18, chúng ta cần xem xét các phần chính sau:
Bài tập 1 yêu cầu… (giả sử bài tập 1 yêu cầu tính giới hạn). Để giải bài tập này, ta sử dụng… (giải thích phương pháp). Cụ thể:
Giải:
… (các bước giải chi tiết)
Vậy, kết quả của bài tập 1 là…
Bài tập 2 yêu cầu… (giả sử bài tập 2 yêu cầu chứng minh một đẳng thức). Để chứng minh đẳng thức này, ta sử dụng… (giải thích phương pháp). Cụ thể:
Giải:
… (các bước giải chi tiết)
Vậy, đẳng thức được chứng minh.
Bài tập 3 yêu cầu… (giả sử bài tập 3 yêu cầu giải phương trình). Để giải phương trình này, ta sử dụng… (giải thích phương pháp). Cụ thể:
Giải:
… (các bước giải chi tiết)
Vậy, nghiệm của phương trình là…
Kiến thức trong mục 3 có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, đặc biệt là trong các bài toán về giới hạn, đạo hàm, tích phân. Việc nắm vững kiến thức này sẽ giúp học sinh giải quyết các bài toán phức tạp một cách hiệu quả.
Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các bạn học sinh đã hiểu rõ hơn về mục 3 trang 17, 18 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các bạn học tập tốt và đạt kết quả cao trong môn Toán!
| Công thức | Mô tả |
|---|---|
| … (Công thức 1) | … (Mô tả công thức 1) |
| … (Công thức 2) | … (Mô tả công thức 2) |