Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh muốn tìm kiếm lời giải bài tập Toán nhanh chóng và chính xác.
Cho ∆ABC đều có cạnh bằng 2. Qua ba phép biến hình liên tiếp: Phép tịnh tiến, phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}},\)
Đề bài
Cho ∆ABC đều có cạnh bằng 2. Qua ba phép biến hình liên tiếp: Phép tịnh tiến, phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}},\) phép vị tự \({V_{\left( {A,{\rm{ }}3} \right)}},\)∆ABC biến thành \(\Delta {A_1}{B_1}{C_1}.\) Tìm diện tích \(\Delta {A_1}{B_1}{C_1}.\)
Phương pháp giải - Xem chi tiết
\({S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}BC.BA.\sin B = \frac{1}{2}CA.CB.\sin C\)
Lời giải chi tiết
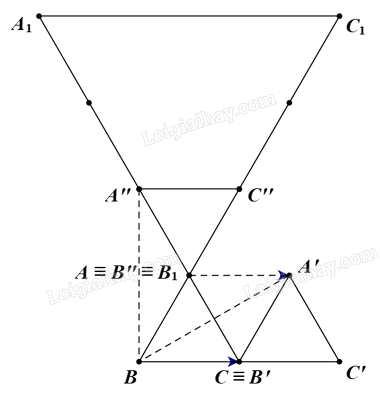
Ta có \(\Delta \)ABC đều có cạnh bằng 2. Suy ra \(AB{\rm{ }} = {\rm{ }}AC{\rm{ }} = {\rm{ }}2\) và \(\widehat {BAC} = {60^o}\).
Vì phép tịnh tiến và phép quay đều là phép dời hình nên ảnh của \(\Delta \)ABC qua phép tịnh tiến \({T_{\overrightarrow {BC} }}\) và phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}}\;\) đều có các kích thước bằng các kích thước tương ứng của \(\Delta \)ABC.
Gọi f là phép biến hình có được bằng thực hiện hai phép biến hình liên tiếp là phép tịnh tiến và phép quay \({Q_{\left( {B,{\rm{ }}60^\circ } \right)}}.\)
Suy ra f là phép dời hình.
Do đó phép đồng dạng tỉ số 3 có được bằng cách thực hiện liên tiếp phép dời hình f và phép vị tự \({V_{(A,{\rm{ }}3)}}\) biến \(\Delta \)ABC thành \(\Delta {A_1}{B_1}{C_1}\).
Vì vậy phép đồng dạng tỉ số 3 biến các điểm A, B, C theo thứ tự thành các điểm \({A_1},{\rm{ }}{B_1},{\rm{ }}{C_1}.\)
Khi đó \({A_1}{B_1}\; = {\rm{ }}3AB{\rm{ }} = {\rm{ }}3.2{\rm{ }} = {\rm{ }}6\) và \({A_1}{C_1}\; = {\rm{ }}3AC{\rm{ }} = {\rm{ }}3.2{\rm{ }} = {\rm{ }}6.\)
Vì \(\Delta \)ABC và \(\Delta \)A1B1C1 đồng dạng với nhau nên \(\widehat {{B_1}{A_1}{C_1}} = \widehat {BAC} = {60^o}\)
Ta có \({S_{\Delta {A_1}{B_1}{C_1}}} = \frac{1}{2}{A_1}{B_1}.{A_1}{C_1}.\sin \widehat {{B_1}{A_1}{C_1}} = \frac{1}{2}.6.6.\sin {60^o} = 9\sqrt 3 \)
Vậy diện tích \(\Delta {A_1}{B_1}{C_1}\) bằng \(9\sqrt 3 \).
Bài 2 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về dãy số, cấp số cộng, cấp số nhân vào giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm, công thức và phương pháp giải liên quan đến dãy số.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo hiệu quả, các em cần:
Dưới đây là lời giải chi tiết bài 2 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo:
(Giả sử đề bài là tìm số hạng thứ 5 của dãy số un = 2n + 1)
Để tìm số hạng thứ 5 của dãy số un = 2n + 1, ta thay n = 5 vào công thức:
u5 = 2 * 5 + 1 = 11
Vậy số hạng thứ 5 của dãy số là 11.
(Giả sử đề bài là tính tổng 10 số hạng đầu tiên của cấp số cộng có u1 = 2 và d = 3)
Để tính tổng 10 số hạng đầu tiên của cấp số cộng, ta sử dụng công thức:
Sn = (n/2) * (2u1 + (n-1)d)
Thay n = 10, u1 = 2 và d = 3 vào công thức, ta được:
S10 = (10/2) * (2 * 2 + (10-1) * 3) = 5 * (4 + 27) = 5 * 31 = 155
Vậy tổng 10 số hạng đầu tiên của cấp số cộng là 155.
Để hiểu rõ hơn về cách giải bài tập về dãy số, chúng ta cùng xem xét một ví dụ minh họa sau:
Ví dụ: Cho dãy số (un) được xác định bởi u1 = 1 và un+1 = un + 2. Tìm số hạng thứ 10 của dãy số.
Lời giải:
Ta có u1 = 1, u2 = u1 + 2 = 3, u3 = u2 + 2 = 5, ...
Nhận thấy dãy số là một cấp số cộng với u1 = 1 và d = 2.
Số hạng thứ n của cấp số cộng được tính bởi công thức: un = u1 + (n-1)d
Vậy số hạng thứ 10 của dãy số là: u10 = 1 + (10-1) * 2 = 1 + 18 = 19
Để củng cố kiến thức và kỹ năng giải bài tập về dãy số, các em có thể luyện tập thêm các bài tập sau:
Bài 2 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp các em hiểu rõ hơn về dãy số và các ứng dụng của nó. Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.