Bài khởi động trang 20 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo là phần mở đầu quan trọng, giúp học sinh ôn lại kiến thức cũ và làm quen với nội dung mới. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự tin giải quyết bài tập.
Chúng tôi hiểu rằng việc học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài tập một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Trong các hình sau, hình nào có tâm đối xứng?
Đề bài
Trong các hình sau, hình nào có tâm đối xứng?
Tồn tại hay không phép biến hình biến mỗi hình phẳng sau đây thành chính nó?
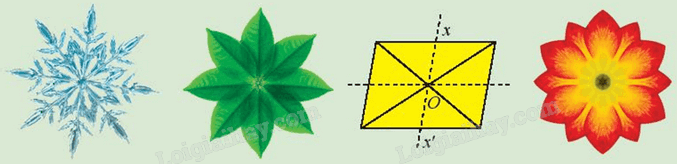
Phương pháp giải - Xem chi tiết
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Lời giải chi tiết
Cả 4 hình đều có tâm đối xứng là điểm O như hình vẽ dưới đây:
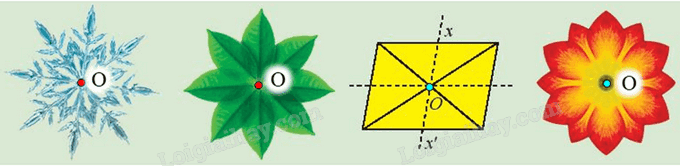
Ta xét hình bông tuyết:
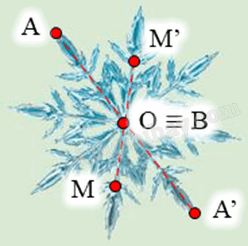
Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.
Lấy điểm A bất kì trên hình bông tuyết sao cho A ≠ O.
Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.
Tương tự như vậy, mỗi điểm M bất kì khác O trên hình bông tuyết, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.
Vì vậy phép biến hình biến hình bông tuyết thành chính nó là phép biến hình biến hình biến điểm O thành chính nó và biến mỗi điểm M khác O thành điểm M’ sao cho O là trung điểm của đoạn MM’.
Chứng minh tương tự với hình 8 chiếc lá, hình bình hành và hình bông hoa, ta cũng được kết quả như trên.
Bài khởi động trang 20 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo đóng vai trò quan trọng trong việc giúp học sinh làm quen với chủ đề mới, củng cố kiến thức nền tảng và phát triển tư duy logic. Bài tập này thường mang tính chất gợi mở, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết vấn đề thực tế.
Bài khởi động trang 20 thường xoay quanh các chủ đề sau (tùy thuộc vào từng chuyên đề cụ thể):
Để giải quyết hiệu quả bài tập khởi động trang 20, học sinh cần:
Bài tập: Cho hàm số y = sin(x). Hãy xác định tập xác định và tập giá trị của hàm số.
Lời giải:
Ngoài dạng bài tập xác định tập xác định và tập giá trị, bài tập khởi động trang 20 còn có thể xuất hiện ở các dạng sau:
Để học tập hiệu quả và đạt kết quả cao trong các bài tập khởi động trang 20, học sinh nên:
Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học Toán hữu ích và nâng cao kết quả học tập của bạn!