Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11 Chuyên đề học tập. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 6 trang 24, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Nghệ thuật cắt giấy Kirigami của Nhật Bản đã sử dụng rất nhiều phép đối xứng khi cắt để tạo ra các hình đẹp. Hãy tìm trục đối xứng và tâm đối xứng của các hình trong Hình 13.
Đề bài
Nghệ thuật cắt giấy Kirigami của Nhật Bản đã sử dụng rất nhiều phép đối xứng khi cắt để tạo ra các hình đẹp. Hãy tìm trục đối xứng và tâm đối xứng của các hình trong Hình 13.

Phương pháp giải - Xem chi tiết
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục qua d biến H thành chính nó.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết
⦁ Trục đối xứng của các hình trong Hình 13:
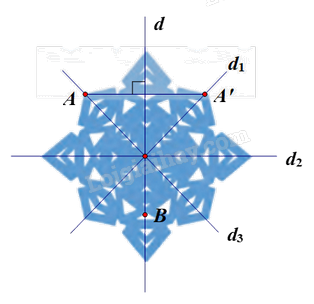
Chọn đường thẳng d trên hoa văn thứ nhất (như hình vẽ).
Lấy điểm A nằm trên hình thứ nhất nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên hình thứ nhất.
Lấy điểm B nằm trên hình thứ nhất và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình thứ nhất, ta đều xác định được ảnh của các điểm đó qua Đd trên hình thứ nhất.
Do đó phép đối xứng trục d biến hình thứ nhất thành chính nó.
Vậy đường thẳng d là trục đối xứng của hình thứ nhất.
Chú ý: Hình hoa văn đầu tiên có 4 trục đối xứng \((d,{\rm{ }}{Đ_1},{\rm{ }}{Đ_2},{\rm{ }}{Đ_3}).\)
Gọi e, f theo thứ tự là đường thẳng nằm trên hình thứ hai và hình thứ ba (hình vẽ).

Chứng minh tương tự như trên, ta cũng xác định được e, f lần lượt là trục đối xứng của hình thứ hai và hình thứ ba.
Chú ý:
– Hình hoa văn thứ hai có 6 trục đối xứng \((e,{\rm{ }}{e_1},{\rm{ }}{e_2},{\rm{ }}{e_3},{\rm{ }}{e_4},{\rm{ }}{e_5}).\)
– Hình hoa văn thứ ba có 6 trục đối xứng \((f,{\rm{ }}{f_1},{\rm{ }}{f_2},{\rm{ }}{f_3},{\rm{ }}{f_4},{\rm{ }}{f_5}).\)
⦁ Tâm đối xứng của các hình trong Hình 13:
Giả sử ta chọn điểm O trên hình đầu tiên (hình vẽ).

Lấy điểm E bất kì trên hình thứ nhất sao cho \(E{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm E’ trên hình thứ nhất sao cho \(E' = {\rm{ }}{Đ_O}\left( E \right).\)
Lấy điểm F trùng O. Khi đó ta có \(F{\rm{ }} = {\rm{ }}{Đ_O}\left( F \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình thứ nhất, ta đều xác định được ảnh của các điểm đó qua ĐO trên hình thứ nhất.
Do đó phép đối xứng tâm O biến hình thứ nhất thành chính nó.
Vậy O là tâm đối xứng của hình thứ nhất.
Chọn I, J theo thứ tự là điểm nằm trên hình thứ hai và hình thứ ba (hình vẽ).

Chứng minh tương tự như trên, ta cũng xác định được I, J lần lượt là tâm đối xứng của hình thứ hai và hình thứ ba.
Bài 6 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số và đồ thị để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số, và cách vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Bài 6 trang 24 thường yêu cầu chúng ta:
Để giúp bạn hiểu rõ hơn về cách giải bài 6 trang 24, chúng ta sẽ cùng nhau đi qua từng bước giải một cách chi tiết. (Nội dung giải bài chi tiết sẽ được trình bày ở đây, bao gồm các bước tính toán, giải thích, và kết luận. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm tập xác định của hàm số f(x) = √(x-2). Để tìm tập xác định, chúng ta cần đảm bảo rằng biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0. Do đó, x-2 ≥ 0, suy ra x ≥ 2. Vậy tập xác định của hàm số là [2, +∞).
Ngoài bài 6 trang 24, Chuyên đề học tập Toán 11 Chân trời sáng tạo còn có rất nhiều bài tập tương tự. Để giải quyết các bài tập này một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Để nâng cao kỹ năng giải toán, bạn nên luyện tập thêm các bài tập tương tự từ sách giáo khoa, sách bài tập, và các nguồn tài liệu trực tuyến khác. Bạn cũng có thể tham gia các khóa học toán online hoặc tìm kiếm sự giúp đỡ từ các giáo viên và bạn bè.
Kiến thức về hàm số và đồ thị có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 6 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt!