Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Tìm các tỉ số vị tự của phép biến hình được thực hiện trên cây thước vẽ truyền trong Hình 13.
Đề bài
Tìm các tỉ số vị tự của phép biến hình được thực hiện trên cây thước vẽ truyền trong Hình 13.
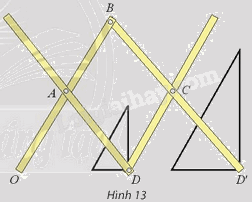
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ và sử dụng hệ quả:
Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|, biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng |k|, biến đường tròn bán kính r thành đường tròn bán kính \(r' = |k|.r\).
Lời giải chi tiết
Xét hình tam giác đỉnh D khi vẽ truyền cho ta hình tam giác đỉnh D’ là ảnh của hình D.
Ta có ba điểm O, D, D’ thẳng hàng nên \(\overrightarrow {OD'} = k\overrightarrow {OD} \).
Do đó \(\;{V_{(O,{\rm{ }}k)}}\left( D \right){\rm{ }} = {\rm{ }}D'\) và \(OD'{\rm{ }} = {\rm{ }}\left| k \right|.OD.\)
Vì D, D’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0.\)
Suy ra \(k = \frac{{OD'}}{{OD}}\)
Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).
Khi đó áp dụng định lí Thales, ta được \(k = \frac{{OD}}{{OD'}} = \frac{{OA}}{{OB}}\)
Vậy phép vị tự biến hình tam giác có đỉnh D thành tam giác có đỉnh D’ là \({V_{\left( {O,\frac{{OA}}{{OB}}} \right)}}\)
Ngược lại, phép vị tự biến hình tam giác đỉnh D’ khi vẽ truyền cho ta hình tam giác đỉnh D là ảnh của hình D là \({V_{\left( {O,\frac{{OB}}{{OA}}} \right)}}\)
Bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 7 trang 36, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập.
Lời giải:
Áp dụng quy tắc tính đạo hàm của tổng và hiệu, ta có:
f'(x) = (x3)' - (3x2)' + (2x)' - (1)'
f'(x) = 3x2 - 6x + 2
Lời giải:
Bước 1: Tính đạo hàm bậc nhất y' = 4x3 - 8x
Bước 2: Tìm các điểm dừng bằng cách giải phương trình y' = 0:
4x3 - 8x = 0
4x(x2 - 2) = 0
Suy ra x = 0, x = √2, x = -√2
Bước 3: Tính đạo hàm bậc hai y'' = 12x2 - 8
Bước 4: Xét dấu đạo hàm bậc hai tại các điểm dừng:
Để giải các bài tập về đạo hàm một cách hiệu quả, các em cần:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn khi giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúc các em học tập tốt!