Bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau:
Đề bài
Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau:
– Lấy một tờ giấy hình vuông, gấp đôi, gấp tư rồi gấp làm tám (Hình 14a).
– Vẽ hoa và lá trên bề mặt tam giác (Hình 14b).
– Dùng kéo cắt theo đường đã vẽ (Hình 14c).
– Trải phẳng tờ giấy ra để thấy hoa văn trang trí gồm hoa và lá (Hình 14d).
Tìm tâm đối xứng và trục đối xứng của hoa văn vừa làm.

Phương pháp giải - Xem chi tiết
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục qua d biến H thành chính nó.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết
⦁ Giả sử ta chọn điểm O là giao điểm của các đường nếp gấp trên hình hoa văn vừa làm (như hình vẽ).

Lấy điểm A bất kì trên hình hoa văn vừa làm sao cho \(A{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm A’ trên hình hoa văn vừa làm sao cho \(A' = {\rm{ }}{Đ_O}\left( A \right).\)
Lấy điểm B trùng O. Khi đó ta có \(B{\rm{ }} = {\rm{ }}{Đ_O}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình hoa văn vừa làm, ta đều xác định được ảnh của các điểm đó qua ĐO trên hình hoa văn vừa làm.
Do đó phép đối xứng tâm O biến hình hoa văn vừa làm thành chính nó.
Vậy O là tâm đối xứng của hình hoa văn vừa làm.
⦁ Giả sử ta chọn đường thẳng d trên hình hoa văn vừa làm như hình vẽ.
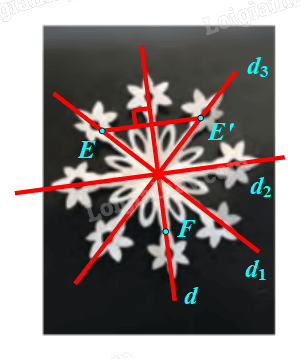
Lấy điểm E trên hình hoa văn vừa làm nhưng không nằm trên đường thẳng d.
Ta đặt \(E' = {\rm{ }}{Đ_d}\left( E \right).\)
Khi đó E’ nằm trên hình hoa văn vừa làm.
Lấy điểm F trên hình hoa văn vừa làm và nằm trên đường thẳng d.
Ta thấy \(F{\rm{ }} = {\rm{ }}{Đ_d}\left( F \right).\)
Tương tự như vậy, ta chọn các điểm khác bất kì trên hình hoa văn vừa làm, ta đều xác định được ảnh của điểm đó qua Đd trên hình hoa văn vừa làm.
Do đó phép đối xứng trục d biến hình hoa văn vừa làm thành chính nó.
Vậy d là trục đối xứng của hình hoa văn vừa làm.
Chú ý: Hình hoa văn vừa làm có 4 trục đối xứng \((d,{\rm{ }}{Đ_1},{\rm{ }}{Đ_2},{\rm{ }}{Đ_3}).\)
Bài 7 trang 25 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Cụ thể, bài toán yêu cầu học sinh xác định và tính toán đạo hàm của hàm số, sau đó sử dụng đạo hàm để tìm ra các giá trị cực trị hoặc giải quyết các bài toán tối ưu hóa đơn giản.
Để giải quyết bài 7 trang 25 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài toán thường bao gồm các bước sau:
(Giả sử đề bài cụ thể của bài 7 là: Cho hàm số f(x) = x^3 - 3x^2 + 2. Tìm các điểm cực trị của hàm số.)
Giải:
1. Tính đạo hàm:
f'(x) = 3x^2 - 6x
2. Tìm điểm cực trị:
Giải phương trình f'(x) = 0:
3x^2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
3. Xác định loại cực trị:
f''(x) = 6x - 6
f''(0) = -6 < 0, vậy x = 0 là điểm cực đại.
f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.
4. Kết luận:
Hàm số f(x) đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số f(x) đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Ngoài bài 7 trang 25, Chuyên đề học tập Toán 11 Chân trời sáng tạo còn có nhiều bài tập tương tự liên quan đến ứng dụng đạo hàm. Các bài tập này có thể yêu cầu học sinh:
Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức và phương pháp đã trình bày ở trên. Ngoài ra, cần luyện tập thường xuyên để rèn luyện kỹ năng và kinh nghiệm giải toán.
Để hỗ trợ quá trình học tập và giải bài tập, học sinh có thể tham khảo các tài liệu sau:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và các hướng dẫn trên sẽ giúp các em học sinh hiểu rõ hơn về bài 7 trang 25 Chuyên đề học tập Toán 11 Chân trời sáng tạo và tự tin hơn trong quá trình học tập.