Bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chuyên đề. Bài tập này thường yêu cầu vận dụng các công thức, định lý và phương pháp giải toán đã được trình bày trong sách giáo khoa.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh có thể tự học và ôn tập hiệu quả.
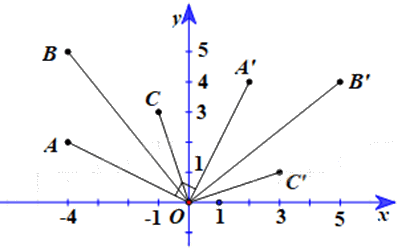
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {-4;{\rm{ }}2} \right),{\rm{ }}B\left( {-4;{\rm{ }}5} \right)\) và \(C\left( {-1;{\rm{ }}3} \right).\)
Đề bài
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {-4;{\rm{ }}2} \right),{\rm{ }}B\left( {-4;{\rm{ }}5} \right)\) và \(C\left( {-1;{\rm{ }}3} \right).\)
a) Chứng minh các điểm \(A'\left( {2;{\rm{ }}4} \right),{\rm{ }}B'\left( {5;{\rm{ }}4} \right){\rm{ }}\) và \(C'\left( {3;{\rm{ }}1} \right)\) theo thứ tự là ảnh của A, B, C qua phép quay tâm O với góc quay –90°.
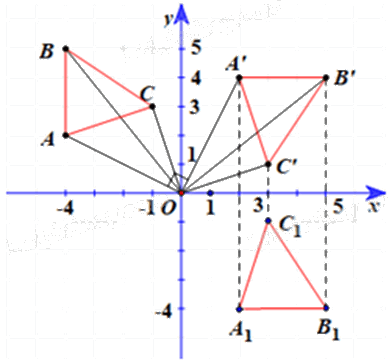
b) Gọi \(\Delta {A_1}{B_1}{C_1}\) là ảnh của ∆ABC qua phép dời hình có được bằng cách thực hiện phép quay tâm O với góc quay –90° và phép đối xứng qua Ox. Tìm tọa độ các đỉnh của \(\Delta {A_1}{B_1}{C_1}.\)
Phương pháp giải - Xem chi tiết
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.
Phép quay tâm O, góc -900: Khi đó: \(\left\{ \begin{array}{l}x' = y\\y' = - x\end{array} \right.\)
Lời giải chi tiết
a)
Với ta có \(\overrightarrow {OA} = \left( { - 4;2} \right),\overrightarrow {OA'} = \left( {2;4} \right),\overrightarrow {AA'} = \left( {6;2} \right)\)
Do đó \(OA = OA' = 2\sqrt 5 \) và \(AA' = 2\sqrt {10} \)
Suy ra \(\cos \widehat {AOA'} = \frac{{O{A^2} + OA{'^2} - AA{'^2}}}{{2.OA.OA'}} = \frac{{{{\left( {2\sqrt 5 } \right)}^2} + {{\left( {2\sqrt 5 } \right)}^2} - {{\left( {2\sqrt {10} } \right)}^2}}}{{2.2\sqrt 5 .2\sqrt 5 }} = 0\)
Do đó \(\widehat {AOA'} = 90^\circ \)
Mà khi quay đoạn OA (với tâm O) theo hướng cùng chiều kim đồng hồ một góc 90° thì ta được đoạn OA’. Tức là, phép quay có góc quay lượng giác theo chiều âm một góc 90°.
Vì vậy góc lượng giác \(\left( {OA,{\rm{ }}OA'} \right){\rm{ }} = {\rm{ }}-90^\circ .\)
Vậy A’ là ảnh của A qua phép quay tâm O với góc quay –90°.
Chứng minh tương tự, ta thu được B’, C’ theo thứ tự là ảnh của B, C qua phép quay tâm O với góc quay –90°.
b) Từ câu a, ta có phép quay tâm O, góc quay –90° biến ∆ABC thành ∆A’B’C’.
Ta có: \(\Delta {A_1}{B_1}{C_1}\;\) là ảnh của ∆A’B’C’ qua phép đối xứng trục Ox nên:
• \({A_1}\; = {\rm{ }}{Đ_{Ox}}\left( {A'} \right),\) do đó hai điểm A1 và A’(2; 4) có cùng hoành độ và có tung độ đối nhau, suy ra A1(2; –4).
• \({B_1}\; = {\rm{ }}{{\rm{Đ}}_{Ox}}\left( {B'} \right),\) do đó hai điểm B1 và B’(5; 4) có cùng hoành độ và có tung độ đối nhau, suy ra B1(5; –4).
• \({C_1}\; = {\rm{ }}{Đ_{Ox}}\left( {C'} \right),\)do đó hai điểm C1 và C’(3; 1) có cùng hoành độ và có tung độ đối nhau, suy ra C1(3; –1).
Vậy tọa độ các đỉnh của ∆A1B1C1 thỏa mãn yêu cầu bài toán là \({A_1}\left( {2;{\rm{ }}-4} \right),{\rm{ }}{B_1}\left( {5;{\rm{ }}-4} \right),{\rm{ }}{C_1}\left( {3;{\rm{ }}-1} \right).\)
Bài 1 trang 28 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc củng cố kiến thức về một chủ đề cụ thể trong chương trình. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm, định lý và phương pháp đã được học. Bài viết này sẽ cung cấp một hướng dẫn chi tiết, từng bước để giải bài tập này, đồng thời giải thích rõ ràng các bước thực hiện.
Trước khi bắt đầu giải bài, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này bao gồm việc xác định các thông tin đã cho, các thông tin cần tìm và các điều kiện ràng buộc. Trong bài 1 trang 28, học sinh cần chú ý đến các yếu tố sau:
Dưới đây là lời giải chi tiết cho bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tính giá trị của biểu thức A = sin2x + cos2x.
Ngoài bài 1 trang 28, Chuyên đề học tập Toán 11 Chân trời sáng tạo còn có nhiều bài tập tương tự khác. Để nâng cao kỹ năng giải toán, học sinh nên luyện tập thêm các bài tập sau:
Để giải các bài tập Toán 11 Chân trời sáng tạo một cách hiệu quả, học sinh có thể áp dụng một số mẹo sau:
Kiến thức về Toán 11 Chân trời sáng tạo có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng rằng với hướng dẫn chi tiết và các mẹo giải toán hiệu quả được trình bày trong bài viết này, các em học sinh sẽ có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| tan x = sin x / cos x | Định nghĩa hàm tan |