Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập khởi động trang 10 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Phép dời hình nào có thể biến hình ngôi sao A thành hình ngôi sao B?
Đề bài
Phép dời hình nào có thể biến hình ngôi sao A thành hình ngôi sao B?

Phương pháp giải - Xem chi tiết
Quan sát hình vẽ và suy luận
Lời giải chi tiết
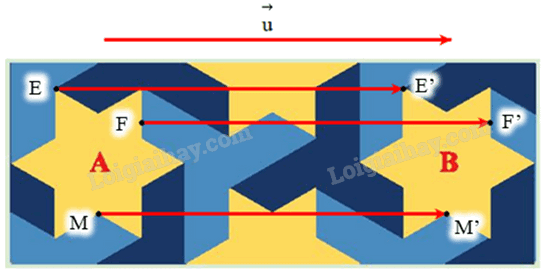
Gọi E là một điểm bất kì trên hình ngôi sao A và E’ là một điểm trên hình ngôi sao B có vị trí tương ứng với điểm E trên hình ngôi sao A (hình vẽ).
Ta đặt \(\vec u = \overrightarrow {EE'} \)
Lấy điểm F bất kì trên hình ngôi sao A sao cho F ≠ E.
Lấy điểm F’ sao cho \(\overrightarrow {FF'} = \vec u\).
Khi đó điểm F’ là một điểm trên hình ngôi sao B có vị trí tương ứng với điểm F trên hình ngôi sao A.
Tương tự như vậy, với mỗi điểm M bất kì trên hình ngôi sao A, ta lấy điểm M’ sao cho \(\overrightarrow {MM'} = \vec u\) thì từ hình ngôi sao A là tập hợp điểm M, ta được tập hợp các điểm M’ tạo thành hình ngôi sao B.
Vậy phép dời hình cần tìm là phép biến hình biến mỗi điểm M bất kì thành điểm M’ sao cho \(\overrightarrow {MM'} = \vec u\).
Bài tập khởi động trang 10 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo đóng vai trò quan trọng trong việc ôn lại kiến thức cũ và đặt nền móng cho các bài học mới. Bài tập này thường tập trung vào việc củng cố các khái niệm cơ bản, các định nghĩa và các tính chất quan trọng đã được học trước đó. Việc giải bài tập này không chỉ giúp học sinh kiểm tra mức độ hiểu bài mà còn rèn luyện kỹ năng vận dụng kiến thức vào thực tế.
Bài tập khởi động trang 10 thường xoay quanh các chủ đề sau:
Để giải bài tập khởi động trang 10 hiệu quả, học sinh cần:
Bài tập: Cho hàm số y = x2 - 4x + 3. Tìm tập xác định và tập giá trị của hàm số.
Giải:
Trong quá trình giải bài tập khởi động, học sinh cần lưu ý:
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp đầy đủ các lời giải bài tập Toán 11, đáp án trắc nghiệm, và các tài liệu học tập hữu ích khác. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em nắm vững kiến thức và đạt kết quả cao trong môn Toán.
| Chuyên đề | Nội dung |
|---|---|
| Hàm số | Giải bài tập, lý thuyết, ví dụ minh họa |
| Đạo hàm | Giải bài tập, lý thuyết, ứng dụng |
| Giới hạn | Giải bài tập, lý thuyết, phương pháp giải |
Hãy truy cập Giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học Toán 11 hữu ích!