Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 Chân trời sáng tạo tại giaitoan.edu.vn.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Chuyên đề học tập Toán 11, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán.
Cùng giaitoan.edu.vn khám phá lời giải mục 1 trang 25, 26, 27 ngay bây giờ!
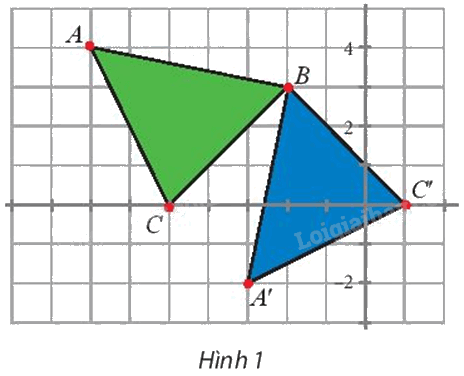
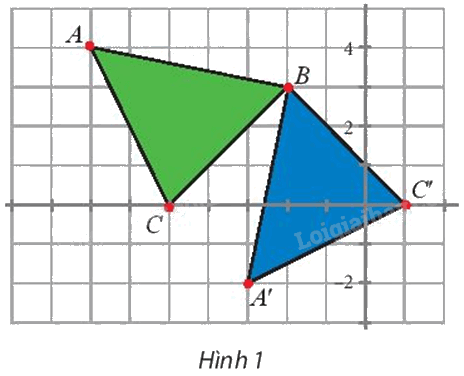
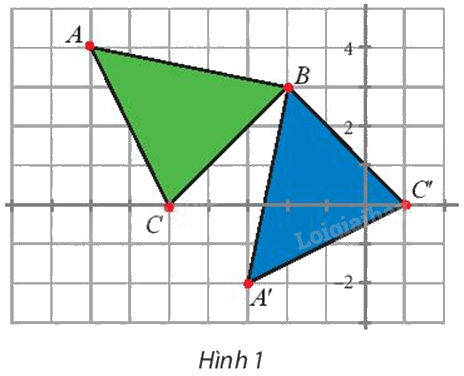
Tìm phép biến hình biến \(\Delta \)BAC thành \(\Delta \)BA’C’ (Hình 1).
Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) lần lượt qua các phép quay \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}180^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}360^\circ } \right)}}.\)
Phương pháp giải:
Phép quay tâm O, góc quay :
Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Lời giải chi tiết:
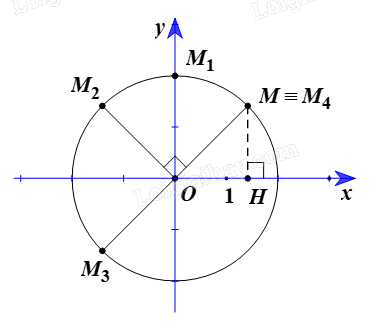
Ta có \(\overrightarrow {OM} = \left( {\sqrt 2 ;\sqrt 2 } \right)\). Suy ra OM = 2.
Vẽ đường tròn (C) tâm O bán kính OM.
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}}\)
Ta có \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}}\) biến điểm M khác O thành điểm M1 sao cho \(O{M_1}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_1}){\rm{ }} = {\rm{ }}45^\circ \) nên \(\widehat {MO{M_1}} = 45^\circ \)
Kẻ \(MH \bot Ox\) tại H.
Tam giác OMH vuông tại H: \(\cos \widehat {MOH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 2 }}{2}\)
Suy ra \(\widehat {MOH} = 45^\circ \)
Ta có \(\widehat {HO{M_1}} = \widehat {HOM} + \widehat {MO{M_1}} = 45^\circ + 45^\circ = 90^\circ \)
Suy ra \({M_1}\; \in {\rm{ }}Oy\) nên \({x_{{M_1}}} = 0\)
Mà \(O{M_1}\; = {\rm{ }}2\) (chứng minh trên) nên tọa độ \({M_1}\left( {0;{\rm{ }}2} \right).\)
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\)
Ta có \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\) biến điểm M khác O thành điểm M2 sao cho \(O{M_2}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_2}){\rm{ }} = {\rm{ }}90^\circ \) nên \(\widehat {MO{M_2}} = 90^\circ \).
Suy ra tam giác \(MO{M_2}\) vuông cân tại O.
Ta có \(\widehat {{M_1}O{M_2}} = \widehat {MO{M_2}} - \widehat {MO{M_1}} = 90^\circ - 45^\circ = 45^\circ \)
Suy ra \(\widehat {MO{M_1}} = \widehat {{M_1}O{M_2}} = 45^\circ \)
Khi đó tam giác MOM2 có OM1 là đường phân giác.
Vì vậy OM1 cũng là đường trung trực của tam giác MOM2 hay Oy là đường trung trực của tam giác MOM2.
Suy ra M2 là ảnh của điểm M qua phép đối xứng trục Oy.
Do đó hai điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) và M2 có cùng tung độ và có hoành độ đối nhau.
Vậy tọa độ \({M_2}\left( { - \sqrt 2 ;\sqrt 2 } \right)\)
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{(O,{\rm{ }}180^\circ )}}\)
Ta có \({Q_{(O,{\rm{ }}180^\circ )}}\) biến điểm M khác O thành điểm M3 sao cho \(O{M_3}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_3}){\rm{ }} = {\rm{ }}180^\circ \) nên \(\widehat {MO{M_3}} = 180^\circ \)
Suy ra O là trung điểm của MM3.
Khi đó \(\left\{ \begin{array}{l}{x_O} = \frac{{{x_M} + {x_{{M_3}}}}}{2}\\{y_O} = \frac{{{y_M} + {y_{{M_3}}}}}{2}\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}{x_{{M_3}}} = 2{x_O} - {x_M} = 2.0 - \sqrt 2 = - \sqrt 2 \\{y_{{M_3}}} = 2{y_O} - {y_M} = 2.0 - \sqrt 2 = - \sqrt 2 \end{array} \right.\)
Vậy tọa độ \({M_3}\left( { - \sqrt 2 ; - \sqrt 2 } \right)\)
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{(O,{\rm{ }}360^\circ )}}\)
Ta có \({Q_{(O,{\rm{ }}360^\circ )}}\) biến điểm M khác O thành điểm M4 sao cho \(O{M_4}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_4}){\rm{ }} = {\rm{ }}360^\circ \) nên \(\widehat {MO{M_4}} = 360^\circ \)
Tức là, \({M_4}\; \equiv M.\)
Vậy tọa độ \({M_4}\left( {\sqrt 2 ;\sqrt 2 } \right)\).
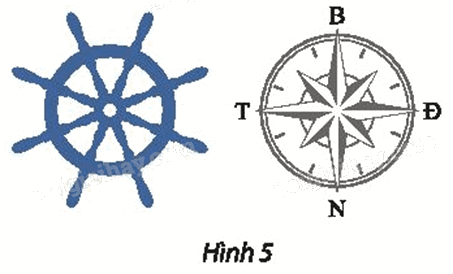
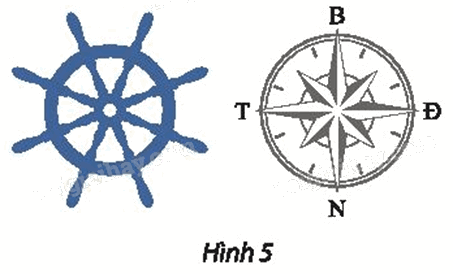
Một con tàu đang di chuyển theo hướng bắc. Người lái tàu phải thực hiện phép quay nào trên bánh lái để con tàu:
a) rẽ sang hướng tây?
b) rẽ sang hướng đông?
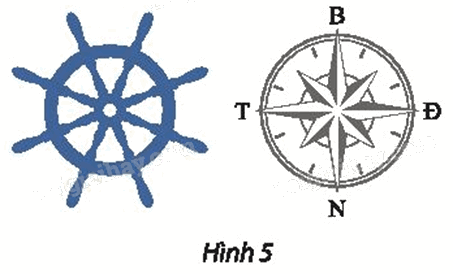
Phương pháp giải:
Quan sát hình 5 và dựa vào đề bài để tìm góc quay φ
Lời giải chi tiết:
a) Để con tàu rẽ sang hướng tây, người lái tàu phải thực hiện phép quay với tâm là tâm của bánh lái và góc quay φ = 90°.
b) Để con tàu rẽ sang hướng đông, người lái tàu phải thực hiện phép quay với tâm là tâm của bánh lái và góc quay φ = –90°.
a) Tìm phép biến hình biến \(\Delta \)BAC thành \(\Delta \)BA’C’ (Hình 1).
b) Trong mặt phẳng, cho điểm O cố định (Hình 2).
Gọi f là quy tắc ứng với mỗi điểm M trùng O cho ta điểm O và ứng với điểm M khác O cho ta một điểm M’ xác định như sau:
– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.
– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng 60°.
Quy tắc f có phải là một phép biến hình không?
Hãy vẽ điểm M’ theo quy tắc trên nếu thay góc 60° bởi góc –30°.
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
a) Để tìm phép biến hình biến ∆BAC thành ∆BA’C’, ta tìm phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’, biến điểm C thành điểm C’.
Với \(\;A\left( {-7;{\rm{ }}4} \right),{\rm{ }}B\left( {-2;{\rm{ }}3} \right),{\rm{ }}C\left( {-5;{\rm{ }}0} \right),{\rm{ }}A'\left( {-3;{\rm{ }}-2} \right),{\rm{ }}C'\left( {1;{\rm{ }}0} \right),\) ta có:
\(\overrightarrow {BA} = \left( { - 5;1} \right),\overrightarrow {BA'} = \left( { - 1; - 5} \right),\overrightarrow {AA'} = \left( {4; - 6} \right)\)
Suy ra \(BA = BA' = \sqrt {26} ;\,AA' = 2\sqrt {13} \)
Khi đó \(\cos \widehat {ABA'} = \frac{{B{A^2} + BA{'^2} - AA{'^2}}}{{2.BA.BA'}} = \frac{{26 + 26 - {{\left( {2\sqrt {13} } \right)}^2}}}{{2.\sqrt {26} .\sqrt {26} }} = 0\)
Vì vậy \(\left( {BA,BA'} \right) = \widehat {ABA'} = 90^\circ \)
Suy ra phép biến hình biến đoạn thẳng BA thành đoạn thẳng BA’ là phép biến hình biến điểm B thành điểm B, biến điểm A thành điểm A’ sao cho BA’ = BA và góc lượng giác \(\left( {BA,{\rm{ }}BA'} \right){\rm{ }} = {\rm{ }}90^\circ {\rm{ }}\left( 1 \right)\)
Thực hiện tương tự, ta được \(BC = BC' = 3\sqrt 2 ;\,\left( {BC,B{C'}} \right) = 90^\circ \)
Suy ra phép biến hình biến đoạn thẳng BC thành đoạn thẳng BC’ là phép biến hình biến điểm B thành điểm B, biến điểm C thành điểm C’ sao cho BC’ = BC và góc lượng giác \(\left( {BC,{\rm{ }}BC'} \right){\rm{ }} = {\rm{ }}90^\circ {\rm{ }}\left( 2 \right)\)
Từ (1), (2), ta thu được phép biến hình biến ∆BAC thành ∆BA’C’ là phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’ sao cho và góc lượng giác \(\left( {BA,{\rm{ }}BA'} \right){\rm{ }} = {\rm{ }}90^\circ \) và biến điểm C thành điểm C’ sao cho \(BC'{\rm{ }} = {\rm{ }}BC\) và góc lượng giác \(\left( {BC,{\rm{ }}BC'} \right){\rm{ }} = {\rm{ }}90^\circ .\)
b) Đặt \({\rm{ }}f\left( M \right){\rm{ }} = {\rm{ }}M'.\) Trong đó, M’ là điểm nằm trên (C) sao cho góc lượng giác \(\left( {OM,{\rm{ }}OM'} \right)\) bằng 60°.
Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
Cách vẽ điểm M’ theo quy tắc trên với góc lượng giác (OM, OM’) bằng –30°:
– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.
– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng –30°.
Ta có hình vẽ sau:

a) Tìm phép biến hình biến \(\Delta \)BAC thành \(\Delta \)BA’C’ (Hình 1).
b) Trong mặt phẳng, cho điểm O cố định (Hình 2).
Gọi f là quy tắc ứng với mỗi điểm M trùng O cho ta điểm O và ứng với điểm M khác O cho ta một điểm M’ xác định như sau:
– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.
– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng 60°.
Quy tắc f có phải là một phép biến hình không?
Hãy vẽ điểm M’ theo quy tắc trên nếu thay góc 60° bởi góc –30°.
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
a) Để tìm phép biến hình biến ∆BAC thành ∆BA’C’, ta tìm phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’, biến điểm C thành điểm C’.
Với \(\;A\left( {-7;{\rm{ }}4} \right),{\rm{ }}B\left( {-2;{\rm{ }}3} \right),{\rm{ }}C\left( {-5;{\rm{ }}0} \right),{\rm{ }}A'\left( {-3;{\rm{ }}-2} \right),{\rm{ }}C'\left( {1;{\rm{ }}0} \right),\) ta có:
\(\overrightarrow {BA} = \left( { - 5;1} \right),\overrightarrow {BA'} = \left( { - 1; - 5} \right),\overrightarrow {AA'} = \left( {4; - 6} \right)\)
Suy ra \(BA = BA' = \sqrt {26} ;\,AA' = 2\sqrt {13} \)
Khi đó \(\cos \widehat {ABA'} = \frac{{B{A^2} + BA{'^2} - AA{'^2}}}{{2.BA.BA'}} = \frac{{26 + 26 - {{\left( {2\sqrt {13} } \right)}^2}}}{{2.\sqrt {26} .\sqrt {26} }} = 0\)
Vì vậy \(\left( {BA,BA'} \right) = \widehat {ABA'} = 90^\circ \)
Suy ra phép biến hình biến đoạn thẳng BA thành đoạn thẳng BA’ là phép biến hình biến điểm B thành điểm B, biến điểm A thành điểm A’ sao cho BA’ = BA và góc lượng giác \(\left( {BA,{\rm{ }}BA'} \right){\rm{ }} = {\rm{ }}90^\circ {\rm{ }}\left( 1 \right)\)
Thực hiện tương tự, ta được \(BC = BC' = 3\sqrt 2 ;\,\left( {BC,B{C'}} \right) = 90^\circ \)
Suy ra phép biến hình biến đoạn thẳng BC thành đoạn thẳng BC’ là phép biến hình biến điểm B thành điểm B, biến điểm C thành điểm C’ sao cho BC’ = BC và góc lượng giác \(\left( {BC,{\rm{ }}BC'} \right){\rm{ }} = {\rm{ }}90^\circ {\rm{ }}\left( 2 \right)\)
Từ (1), (2), ta thu được phép biến hình biến ∆BAC thành ∆BA’C’ là phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’ sao cho và góc lượng giác \(\left( {BA,{\rm{ }}BA'} \right){\rm{ }} = {\rm{ }}90^\circ \) và biến điểm C thành điểm C’ sao cho \(BC'{\rm{ }} = {\rm{ }}BC\) và góc lượng giác \(\left( {BC,{\rm{ }}BC'} \right){\rm{ }} = {\rm{ }}90^\circ .\)
b) Đặt \({\rm{ }}f\left( M \right){\rm{ }} = {\rm{ }}M'.\) Trong đó, M’ là điểm nằm trên (C) sao cho góc lượng giác \(\left( {OM,{\rm{ }}OM'} \right)\) bằng 60°.
Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
Cách vẽ điểm M’ theo quy tắc trên với góc lượng giác (OM, OM’) bằng –30°:
– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.
– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng –30°.
Ta có hình vẽ sau:

Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) lần lượt qua các phép quay \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}180^\circ } \right)}},{\rm{ }}{Q_{\left( {O,{\rm{ }}360^\circ } \right)}}.\)
Phương pháp giải:
Phép quay tâm O, góc quay :
Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Lời giải chi tiết:
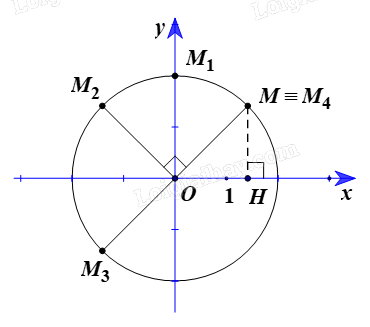
Ta có \(\overrightarrow {OM} = \left( {\sqrt 2 ;\sqrt 2 } \right)\). Suy ra OM = 2.
Vẽ đường tròn (C) tâm O bán kính OM.
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}}\)
Ta có \({Q_{\left( {O,{\rm{ }}45^\circ } \right)}}\) biến điểm M khác O thành điểm M1 sao cho \(O{M_1}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_1}){\rm{ }} = {\rm{ }}45^\circ \) nên \(\widehat {MO{M_1}} = 45^\circ \)
Kẻ \(MH \bot Ox\) tại H.
Tam giác OMH vuông tại H: \(\cos \widehat {MOH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 2 }}{2}\)
Suy ra \(\widehat {MOH} = 45^\circ \)
Ta có \(\widehat {HO{M_1}} = \widehat {HOM} + \widehat {MO{M_1}} = 45^\circ + 45^\circ = 90^\circ \)
Suy ra \({M_1}\; \in {\rm{ }}Oy\) nên \({x_{{M_1}}} = 0\)
Mà \(O{M_1}\; = {\rm{ }}2\) (chứng minh trên) nên tọa độ \({M_1}\left( {0;{\rm{ }}2} \right).\)
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\)
Ta có \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\) biến điểm M khác O thành điểm M2 sao cho \(O{M_2}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_2}){\rm{ }} = {\rm{ }}90^\circ \) nên \(\widehat {MO{M_2}} = 90^\circ \).
Suy ra tam giác \(MO{M_2}\) vuông cân tại O.
Ta có \(\widehat {{M_1}O{M_2}} = \widehat {MO{M_2}} - \widehat {MO{M_1}} = 90^\circ - 45^\circ = 45^\circ \)
Suy ra \(\widehat {MO{M_1}} = \widehat {{M_1}O{M_2}} = 45^\circ \)
Khi đó tam giác MOM2 có OM1 là đường phân giác.
Vì vậy OM1 cũng là đường trung trực của tam giác MOM2 hay Oy là đường trung trực của tam giác MOM2.
Suy ra M2 là ảnh của điểm M qua phép đối xứng trục Oy.
Do đó hai điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) và M2 có cùng tung độ và có hoành độ đối nhau.
Vậy tọa độ \({M_2}\left( { - \sqrt 2 ;\sqrt 2 } \right)\)
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{(O,{\rm{ }}180^\circ )}}\)
Ta có \({Q_{(O,{\rm{ }}180^\circ )}}\) biến điểm M khác O thành điểm M3 sao cho \(O{M_3}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_3}){\rm{ }} = {\rm{ }}180^\circ \) nên \(\widehat {MO{M_3}} = 180^\circ \)
Suy ra O là trung điểm của MM3.
Khi đó \(\left\{ \begin{array}{l}{x_O} = \frac{{{x_M} + {x_{{M_3}}}}}{2}\\{y_O} = \frac{{{y_M} + {y_{{M_3}}}}}{2}\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}{x_{{M_3}}} = 2{x_O} - {x_M} = 2.0 - \sqrt 2 = - \sqrt 2 \\{y_{{M_3}}} = 2{y_O} - {y_M} = 2.0 - \sqrt 2 = - \sqrt 2 \end{array} \right.\)
Vậy tọa độ \({M_3}\left( { - \sqrt 2 ; - \sqrt 2 } \right)\)
⦁ Ảnh của điểm \(M\left( {\sqrt 2 ;\sqrt 2 } \right)\) qua phép quay \({Q_{(O,{\rm{ }}360^\circ )}}\)
Ta có \({Q_{(O,{\rm{ }}360^\circ )}}\) biến điểm M khác O thành điểm M4 sao cho \(O{M_4}\; = {\rm{ }}OM{\rm{ }} = {\rm{ }}2\)và \((OM,{\rm{ }}O{M_4}){\rm{ }} = {\rm{ }}360^\circ \) nên \(\widehat {MO{M_4}} = 360^\circ \)
Tức là, \({M_4}\; \equiv M.\)
Vậy tọa độ \({M_4}\left( {\sqrt 2 ;\sqrt 2 } \right)\).
Một con tàu đang di chuyển theo hướng bắc. Người lái tàu phải thực hiện phép quay nào trên bánh lái để con tàu:
a) rẽ sang hướng tây?
b) rẽ sang hướng đông?
Phương pháp giải:
Quan sát hình 5 và dựa vào đề bài để tìm góc quay φ
Lời giải chi tiết:
a) Để con tàu rẽ sang hướng tây, người lái tàu phải thực hiện phép quay với tâm là tâm của bánh lái và góc quay φ = 90°.
b) Để con tàu rẽ sang hướng đông, người lái tàu phải thực hiện phép quay với tâm là tâm của bánh lái và góc quay φ = –90°.
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào các kiến thức cơ bản về dãy số, cấp số cộng, cấp số nhân. Việc nắm vững các khái niệm và công thức trong mục này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Trang 25 tập trung vào các bài tập vận dụng kiến thức về dãy số để xác định số hạng, tính tổng và phân tích tính chất của dãy số. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 1 yêu cầu xác định dãy số 2, 6, 10, 14,... có phải là cấp số cộng hay không. Để giải bài tập này, ta tính hiệu giữa hai số hạng liên tiếp: 6 - 2 = 4, 10 - 6 = 4, 14 - 10 = 4. Vì hiệu giữa hai số hạng liên tiếp là một hằng số, nên dãy số này là cấp số cộng với công sai d = 4.
Trang 26 tiếp tục củng cố kiến thức về cấp số cộng và cấp số nhân thông qua các bài tập phức tạp hơn. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 2 yêu cầu tìm số hạng thứ 10 của cấp số cộng có số hạng đầu u1 = 3 và công sai d = 2. Để giải bài tập này, ta sử dụng công thức số hạng tổng quát của cấp số cộng: un = u1 + (n - 1)d. Thay u1 = 3, d = 2 và n = 10 vào công thức, ta được u10 = 3 + (10 - 1) * 2 = 21.
Trang 27 tập trung vào các bài tập ứng dụng kiến thức về dãy số và cấp số vào giải quyết các bài toán thực tế. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 3 yêu cầu tính số tiền lãi sau 5 năm nếu gửi tiết kiệm 10 triệu đồng với lãi suất 6%/năm. Để giải bài tập này, ta sử dụng công thức tính lãi kép: A = P(1 + r)^n, trong đó A là số tiền sau n năm, P là số tiền gốc, r là lãi suất hàng năm và n là số năm. Thay P = 10 triệu, r = 6% = 0.06 và n = 5 vào công thức, ta được A = 10(1 + 0.06)^5 ≈ 13.38 triệu đồng. Vậy số tiền lãi sau 5 năm là 13.38 - 10 = 3.38 triệu đồng.
Để giải bài tập về dãy số và cấp số hiệu quả, các em cần:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập trong Mục 1 trang 25, 26, 27 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!