Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 22, 23 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.
Trong Hình 10, hình nào có tâm đối xứng? (Mỗi chữ cái là một hình).

Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
⦁ Giả sử O là một điểm trên hình chữ S (hình vẽ).
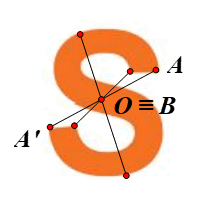
Lấy điểm A bất kì trên hình chữ S sao cho \(A{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm A’ trên hình chữ S sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right).\)
Lấy điểm B trùng O. Khi đó
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình chữ S, ta đều xác định được ảnh của các điểm đó qua ĐO trên hình chữ S.
Vì vậy O là tâm đối xứng của hình chữ S.
⦁ Giả sử O là một điểm trên hình chữ H (hình vẽ).
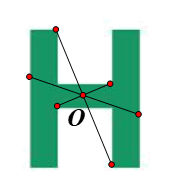
Chứng minh tương tự như trên, ta được O là tâm đối xứng của hình chữ H.
⦁ Các hình còn lại không có tâm đối xứng.
Vậy hình chữ S và hình chữ H có tâm đối xứng là điểm O như hình vẽ.
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.
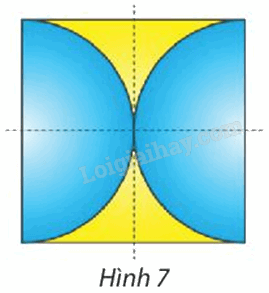
Phương pháp giải:
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục qua d biến H thành chính nó.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
⦁ Giả sử ta chọn đường thẳng d trên Hình 7 như hình vẽ.

Lấy điểm A nằm trên Hình 7 nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên Hình 7 ban đầu.
Lấy điểm B nằm trên Hình 7 và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì trên Hình 7, ta đều xác định được ảnh của các điểm đó qua \({Đ_d}\) trên Hình 7.
Vậy phép đối xứng trục d biến Hình 7 thành chính nó.
Giả sử ta chọn đường thẳng d’ trên Hình 7 như hình vẽ.
Chứng minh tương tự như trên, ta cũng xác định được phép đối xứng trục d’ biến Hình 7 thành chính nó.
⦁ Giả sử ta chọn điểm O trên Hình 7 như hình vẽ.
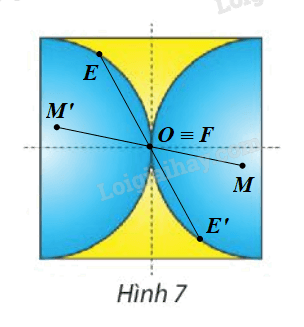
Lấy điểm F trùng O. Khi đó qua O, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên Hình 7 sao cho \(E{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm E’ trên Hình 7 sao cho O là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên Hình 7, ta đều xác định được một điểm M’ trên Hình 7 sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến Hình 7 thành chính nó.
a) Trong Hình 9, hình nào có tâm đối xứng? Tìm tâm đối xứng (nếu có).
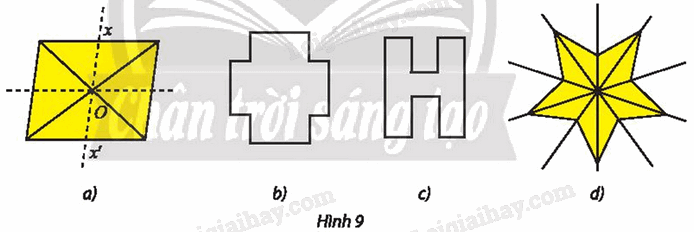
b) Nêu tên một hình có vô số tâm đối xứng.
Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
a) ⦁ Hình 9a:
Ta đặt hình bình hành ở Hình 9a có các đỉnh là A, B, C, D (hình vẽ).
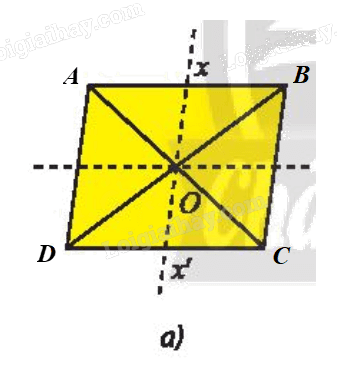
Hình bình hành ABCD có tâm O là giao điểm hai đường chéo.
Suy ra O là trung điểm của AC, do đó \(C{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right),A{\rm{ }} = {\rm{ }}{Đ_O}\left( C \right).\)
Chứng minh tương tự, ta được \(B{\rm{ }} = {\rm{ }}{Đ_O}\left( D \right),D{\rm{ }} = {\rm{ }}{Đ_O}\left( B \right).\)
Do đó ảnh của hình bình hành ABCD qua \({Đ_O}\) là chính nó.
Vậy O là tâm đối xứng của Hình 9a.
⦁ Hình 9b:

Giả sử I là một điểm trên Hình 9b (hình vẽ).
Lấy điểm A bất kì trên Hình 9b sao cho \(A{\rm{ }} \ne {\rm{ }}I.\)
Khi đó ta luôn xác định được một điểm A’ trên Hình 9b sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_I}\left( A \right).\)
Lấy điểm B trùng I. Khi đó \(B{\rm{ }} = {\rm{ }}{Đ_I}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì nằm trên Hình 9b, ta đều xác định được ảnh của các điểm đó qua ĐI trên Hình 9b.
Vậy I là tâm đối xứng của Hình 9b.
⦁ Hình 9c:
Chứng minh tương tự Hình 9b, ta được G là tâm đối xứng của Hình 9c.
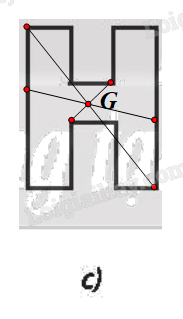
⦁ Hình 9d không có tâm đối xứng.
b) Hình có vô số tâm đối xứng là:
– Đường thẳng: do đường thẳng không có điểm đầu và điểm cuối nên mỗi điểm bất kì nằm trên đường thẳng đều là tâm đối xứng của đường thẳng đó;
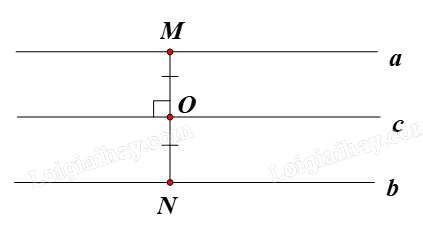
– Hình gồm hai đường thẳng song song: tâm đối xứng của hình gồm hai đường thẳng song song luôn di động trên một đường thẳng cố định, đường thẳng đó là trục đối xứng của hai đường thẳng đã cho.
Cụ thể, giả sử O là tâm đối xứng của hai đường thẳng song song a và b. Khi đó O di động trên đường thẳng c là trục đối xứng của hai đường thẳng a và b.
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.

Phương pháp giải:
Đường thẳng d gọi là trục đối xứng của hình H nếu phép đối xứng trục qua d biến H thành chính nó.
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
⦁ Giả sử ta chọn đường thẳng d trên Hình 7 như hình vẽ.
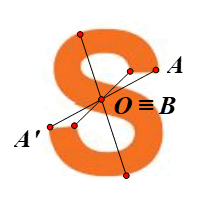
Lấy điểm A nằm trên Hình 7 nhưng không nằm trên đường thẳng d.
Ta đặt \(A'{\rm{ }} = {\rm{ }}{Đ_d}\left( A \right).\)
Khi đó A’ nằm trên Hình 7 ban đầu.
Lấy điểm B nằm trên Hình 7 và nằm trên đường thẳng d.
Ta thấy \(B{\rm{ }} = {\rm{ }}{Đ_d}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì trên Hình 7, ta đều xác định được ảnh của các điểm đó qua \({Đ_d}\) trên Hình 7.
Vậy phép đối xứng trục d biến Hình 7 thành chính nó.
Giả sử ta chọn đường thẳng d’ trên Hình 7 như hình vẽ.
Chứng minh tương tự như trên, ta cũng xác định được phép đối xứng trục d’ biến Hình 7 thành chính nó.
⦁ Giả sử ta chọn điểm O trên Hình 7 như hình vẽ.
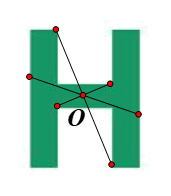
Lấy điểm F trùng O. Khi đó qua O, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên Hình 7 sao cho \(E{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm E’ trên Hình 7 sao cho O là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên Hình 7, ta đều xác định được một điểm M’ trên Hình 7 sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến Hình 7 thành chính nó.
a) Trong Hình 9, hình nào có tâm đối xứng? Tìm tâm đối xứng (nếu có).
b) Nêu tên một hình có vô số tâm đối xứng.
Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
a) ⦁ Hình 9a:
Ta đặt hình bình hành ở Hình 9a có các đỉnh là A, B, C, D (hình vẽ).
Hình bình hành ABCD có tâm O là giao điểm hai đường chéo.
Suy ra O là trung điểm của AC, do đó \(C{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right),A{\rm{ }} = {\rm{ }}{Đ_O}\left( C \right).\)
Chứng minh tương tự, ta được \(B{\rm{ }} = {\rm{ }}{Đ_O}\left( D \right),D{\rm{ }} = {\rm{ }}{Đ_O}\left( B \right).\)
Do đó ảnh của hình bình hành ABCD qua \({Đ_O}\) là chính nó.
Vậy O là tâm đối xứng của Hình 9a.
⦁ Hình 9b:

Giả sử I là một điểm trên Hình 9b (hình vẽ).
Lấy điểm A bất kì trên Hình 9b sao cho \(A{\rm{ }} \ne {\rm{ }}I.\)
Khi đó ta luôn xác định được một điểm A’ trên Hình 9b sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_I}\left( A \right).\)
Lấy điểm B trùng I. Khi đó \(B{\rm{ }} = {\rm{ }}{Đ_I}\left( B \right).\)
Tương tự như vậy, ta chọn các điểm bất kì nằm trên Hình 9b, ta đều xác định được ảnh của các điểm đó qua ĐI trên Hình 9b.
Vậy I là tâm đối xứng của Hình 9b.
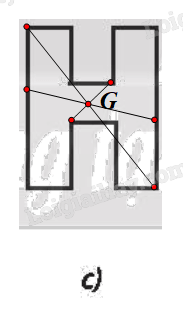
⦁ Hình 9c:
Chứng minh tương tự Hình 9b, ta được G là tâm đối xứng của Hình 9c.
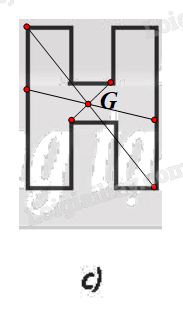
⦁ Hình 9d không có tâm đối xứng.
b) Hình có vô số tâm đối xứng là:
– Đường thẳng: do đường thẳng không có điểm đầu và điểm cuối nên mỗi điểm bất kì nằm trên đường thẳng đều là tâm đối xứng của đường thẳng đó;
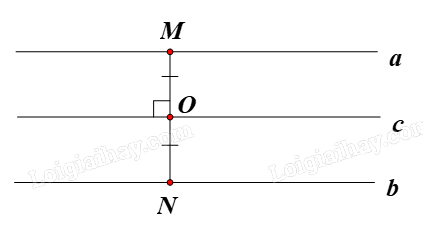
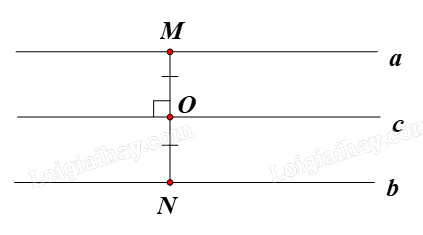
– Hình gồm hai đường thẳng song song: tâm đối xứng của hình gồm hai đường thẳng song song luôn di động trên một đường thẳng cố định, đường thẳng đó là trục đối xứng của hai đường thẳng đã cho.
Cụ thể, giả sử O là tâm đối xứng của hai đường thẳng song song a và b. Khi đó O di động trên đường thẳng c là trục đối xứng của hai đường thẳng a và b.
Trong Hình 10, hình nào có tâm đối xứng? (Mỗi chữ cái là một hình).

Phương pháp giải:
Điểm O được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm O biến hình H thành chính nó.
Lời giải chi tiết:
⦁ Giả sử O là một điểm trên hình chữ S (hình vẽ).
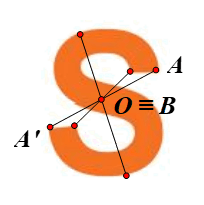
Lấy điểm A bất kì trên hình chữ S sao cho \(A{\rm{ }} \ne {\rm{ }}O.\)
Khi đó ta luôn xác định được một điểm A’ trên hình chữ S sao cho \(A'{\rm{ }} = {\rm{ }}{Đ_O}\left( A \right).\)
Lấy điểm B trùng O. Khi đó
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình chữ S, ta đều xác định được ảnh của các điểm đó qua ĐO trên hình chữ S.
Vì vậy O là tâm đối xứng của hình chữ S.
⦁ Giả sử O là một điểm trên hình chữ H (hình vẽ).
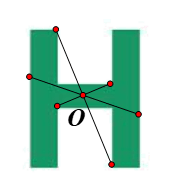
Chứng minh tương tự như trên, ta được O là tâm đối xứng của hình chữ H.
⦁ Các hình còn lại không có tâm đối xứng.
Vậy hình chữ S và hình chữ H có tâm đối xứng là điểm O như hình vẽ.
Mục 3 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững kiến thức nền tảng và các công thức liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, kèm theo các giải thích rõ ràng để giúp học sinh hiểu rõ phương pháp giải.
Để đảm bảo tính chính xác và dễ hiểu, chúng ta sẽ đi qua từng bài tập trong mục 3 trang 22, 23. Mỗi bài tập sẽ được trình bày theo cấu trúc sau:
Đề bài: (Nội dung bài tập 1)
Phân tích đề bài: (Phân tích bài tập 1)
Lời giải: (Lời giải chi tiết bài tập 1)
Kết luận: (Kết quả bài tập 1)
Đề bài: (Nội dung bài tập 2)
Phân tích đề bài: (Phân tích bài tập 2)
Lời giải: (Lời giải chi tiết bài tập 2)
Kết luận: (Kết quả bài tập 2)
Đề bài: (Nội dung bài tập 3)
Phân tích đề bài: (Phân tích bài tập 3)
Lời giải: (Lời giải chi tiết bài tập 3)
Kết luận: (Kết quả bài tập 3)
Kiến thức được học trong mục 3 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, không chỉ trong Toán học mà còn trong các môn học khác như Vật lý, Hóa học, Kinh tế,... Việc nắm vững kiến thức này sẽ giúp học sinh giải quyết các bài toán thực tế một cách hiệu quả.
Để hiểu sâu hơn về nội dung của mục 3, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những lời giải chi tiết và hữu ích cho mục 3 trang 22, 23 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!