Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 Chuyên đề học tập - Chân trời sáng tạo. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 8, 9 và 10 của chuyên đề.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán khó.
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
Gọi A’B’C’D’ là ảnh của hình chữ nhật ABCD qua phép biến hình được diễn tả trong Vận dụng. Hãy cho biết A’B’C’D’ là hình gì. Giải thích.
Phương pháp giải:
Phép dời hình bảo toàn:
- Tính thẳng hàng của 3 điểm và thứ tự của ba điểm thẳng hàng.
- Tính song song của hai đường thẳng.
- Độ lớn của một góc.
Lời giải chi tiết:
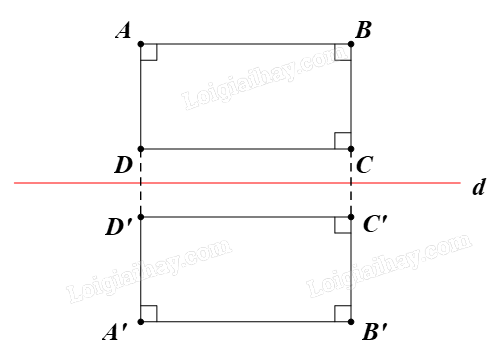
Gọi f là phép biến hình trong Vận dụng.
Trong Vận dụng, ta đã chứng minh được f là một phép dời hình.
Ta có ABCD là hình chữ nhật.
Suy ra \(\;\widehat {DAB} = 90^\circ ;\,\,\widehat {ABC} = 90^\circ ;\,\,\widehat {BCD} = 90^\circ \)
Do phép dời hình f bảo toàn độ lớn của góc nên ta có \(\widehat {{\rm{D'A'B'}}} = 90^\circ ;\widehat {{\rm{A'B'C'}}} = 90^\circ ;\widehat {{\rm{B'C'D'}}} = 90^\circ \)
Vậy A’B’C’D’ cũng là hình chữ nhật.
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
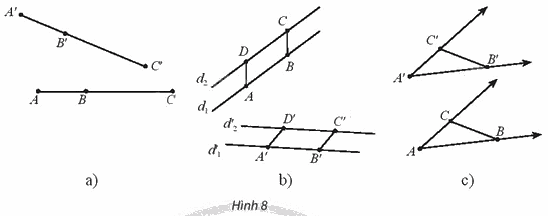
a) Cho ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C). Gọi A’, B’, C’ lần lượt là ảnh của A, B, C qua f (Hình 8a). Có nhận xét gì về vị trí tương đối của ba điểm A’, B’, C’?
b) Cho hai đường thẳng song song d1 và d2, lấy hai đoạn thẳng bằng nhau AB và DC lần lượt trên d1 và d2. Gọi \({d_1}',{d_2}'\) lần lượt là ảnh của d1, d2 và A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua f (Hình 8b). Tứ giác A’B’C’D’ là hình gì? Nêu nhận xét về vị trí tương đối của hai đường thẳng \({d_1}',{d_2}'\).
c) Cho A’B’C’ là ảnh của tam giác ABC qua f (Hình 8c).
So sánh và \(\Delta ABC\). So sánh số đo hai góc \(\widehat {BAC}\) và \(\widehat {B'A'C'}\).
Phương pháp giải:
Quan sát hình 8 để trả lời
Lời giải chi tiết:
Phép dời hình f bảo toàn khoảng cách giữa hai điểm bất kì.
a) Ta có A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Suy ra A’B’ = AB; B’C’ = BC và A’C’ = AC.
Theo đề, ta có ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C).
Suy ra AB + BC = AC.
Khi đó A’B’ + B’C’ = A’C’.
Vậy ba điểm A’, B’, C’ thẳng hàng theo thứ tự (B’ nằm giữa A’ và C’).
b) Ta có AB = DC (giả thiết) và AB // DC (do d1 // d2).
Suy ra tứ giác ABCD là hình bình hành.
Khi đó AD = BC.
Ta có A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua phép dời hình f.
Suy ra A’B’ = AB; D’C’ = DC.
Mà AB = DC (giả thiết), do đó A’B’ = D’C’ (1)
Chứng minh tương tự, ta được A’D’ = B’C’ (2)
Từ (1), (2), suy ra tứ giác A’B’C’D’ là hình bình hành.
Khi đó A’B’ // D’C’ hay \({d_1}'{\rm{//}}{d_2}'\).
Vậy tứ giác A’B’C’D’ là hình bình hành và \({d_1}'{\rm{//}}{d_2}'\).
c) Ta có tam giác A’B’C’ là ảnh của tam giác ABC qua phép dời hình f.
Suy ra A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Vì vậy A’B’ = AB; B’C’ = BC và A’C’ = AC.
Do đó ∆A’B’C’ = ∆ABC (c.c.c).
Từ đó suy ra \(\widehat {B'A'C'} = \widehat {BAC}\) (cặp cạnh tương ứng).
Vậy \(\Delta A'B'C'{\rm{ }} = {\rm{ }}\Delta ABC\) và \(\widehat {B'A'C'} = \widehat {BAC}\).
Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.
a) Cho ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C). Gọi A’, B’, C’ lần lượt là ảnh của A, B, C qua f (Hình 8a). Có nhận xét gì về vị trí tương đối của ba điểm A’, B’, C’?
b) Cho hai đường thẳng song song d1 và d2, lấy hai đoạn thẳng bằng nhau AB và DC lần lượt trên d1 và d2. Gọi \({d_1}',{d_2}'\) lần lượt là ảnh của d1, d2 và A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua f (Hình 8b). Tứ giác A’B’C’D’ là hình gì? Nêu nhận xét về vị trí tương đối của hai đường thẳng \({d_1}',{d_2}'\).
c) Cho A’B’C’ là ảnh của tam giác ABC qua f (Hình 8c).
So sánh và \(\Delta ABC\). So sánh số đo hai góc \(\widehat {BAC}\) và \(\widehat {B'A'C'}\).
Phương pháp giải:
Quan sát hình 8 để trả lời
Lời giải chi tiết:
Phép dời hình f bảo toàn khoảng cách giữa hai điểm bất kì.
a) Ta có A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Suy ra A’B’ = AB; B’C’ = BC và A’C’ = AC.
Theo đề, ta có ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C).
Suy ra AB + BC = AC.
Khi đó A’B’ + B’C’ = A’C’.
Vậy ba điểm A’, B’, C’ thẳng hàng theo thứ tự (B’ nằm giữa A’ và C’).
b) Ta có AB = DC (giả thiết) và AB // DC (do d1 // d2).
Suy ra tứ giác ABCD là hình bình hành.
Khi đó AD = BC.
Ta có A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua phép dời hình f.
Suy ra A’B’ = AB; D’C’ = DC.
Mà AB = DC (giả thiết), do đó A’B’ = D’C’ (1)
Chứng minh tương tự, ta được A’D’ = B’C’ (2)
Từ (1), (2), suy ra tứ giác A’B’C’D’ là hình bình hành.
Khi đó A’B’ // D’C’ hay \({d_1}'{\rm{//}}{d_2}'\).
Vậy tứ giác A’B’C’D’ là hình bình hành và \({d_1}'{\rm{//}}{d_2}'\).
c) Ta có tam giác A’B’C’ là ảnh của tam giác ABC qua phép dời hình f.
Suy ra A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.
Vì vậy A’B’ = AB; B’C’ = BC và A’C’ = AC.
Do đó ∆A’B’C’ = ∆ABC (c.c.c).
Từ đó suy ra \(\widehat {B'A'C'} = \widehat {BAC}\) (cặp cạnh tương ứng).
Vậy \(\Delta A'B'C'{\rm{ }} = {\rm{ }}\Delta ABC\) và \(\widehat {B'A'C'} = \widehat {BAC}\).
Gọi A’B’C’D’ là ảnh của hình chữ nhật ABCD qua phép biến hình được diễn tả trong Vận dụng. Hãy cho biết A’B’C’D’ là hình gì. Giải thích.
Phương pháp giải:
Phép dời hình bảo toàn:
- Tính thẳng hàng của 3 điểm và thứ tự của ba điểm thẳng hàng.
- Tính song song của hai đường thẳng.
- Độ lớn của một góc.
Lời giải chi tiết:
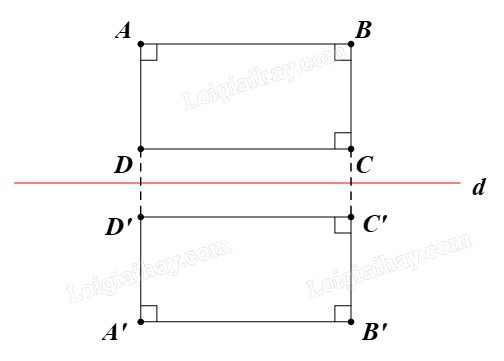
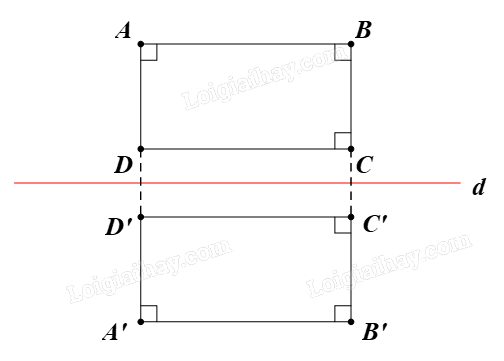
Gọi f là phép biến hình trong Vận dụng.
Trong Vận dụng, ta đã chứng minh được f là một phép dời hình.
Ta có ABCD là hình chữ nhật.
Suy ra \(\;\widehat {DAB} = 90^\circ ;\,\,\widehat {ABC} = 90^\circ ;\,\,\widehat {BCD} = 90^\circ \)
Do phép dời hình f bảo toàn độ lớn của góc nên ta có \(\widehat {{\rm{D'A'B'}}} = 90^\circ ;\widehat {{\rm{A'B'C'}}} = 90^\circ ;\widehat {{\rm{B'C'D'}}} = 90^\circ \)
Vậy A’B’C’D’ cũng là hình chữ nhật.
Mục 3 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 11, là nền tảng cho các kiến thức nâng cao hơn trong chương trình học. Việc nắm vững các khái niệm và kỹ năng giải bài tập trong mục này là rất cần thiết để đạt kết quả tốt trong các kỳ thi.
Mục 3 bao gồm các nội dung chính sau:
Trang 8 tập trung vào việc vận dụng định nghĩa đạo hàm để tính đạo hàm của một số hàm số đơn giản. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài 1 yêu cầu tính đạo hàm của hàm số f(x) = x2 tại x = 2. Lời giải:
f'(x) = limh→0 (f(x+h) - f(x))/h = limh→0 ((x+h)2 - x2)/h = limh→0 (2xh + h2)/h = 2x
Vậy f'(2) = 2*2 = 4
Trang 9 giới thiệu các quy tắc tính đạo hàm. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài 3 yêu cầu tính đạo hàm của hàm số y = (x2 + 1)(x - 2). Lời giải:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Trang 10 tập trung vào việc tính đạo hàm của các hàm số sơ cấp. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài 5 yêu cầu tính đạo hàm của hàm số y = sin(x2). Lời giải:
y' = cos(x2) * 2x = 2xcos(x2)
Hy vọng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 3 trang 8, 9, 10 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!