Bài 5 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh phải vận dụng kiến thức đã học để tìm đạo hàm, xét dấu đạo hàm và xác định các điểm cực trị của hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC với B và C cố định. Vẽ hai đường tròn có tâm lần lượt là B, C và đi qua A
Đề bài
Cho tam giác ABC với B và C cố định. Vẽ hai đường tròn có tâm lần lượt là B, C và đi qua A. Gọi D là giao điểm thứ hai của hai đường tròn nói trên (Hình 12). Khi A di động trên một đường tròn cố định (O) thì điểm D di động trên đường nào?
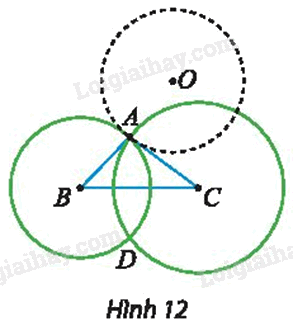
Phương pháp giải - Xem chi tiết
Suy luận để tìm ra mối quan hệ giữa điểm A và D.
Lời giải chi tiết
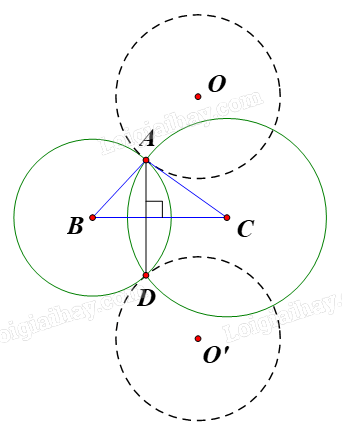
Gọi đường tròn (O’) là ảnh của đường tròn (O) qua \({Đ_{BC}}.\)
Ta có đường tròn tâm B và đường tròn tâm C cắt nhau tại hai điểm A và D.
Suy ra BC là đường trung trực của đoạn AD.
Do đó D là ảnh của A qua \({Đ_{BC}}.\)
Vậy khi điểm A di động trên đường tròn cố định (O) thì điểm D di động trên đường tròn cố định (O’), với (O’) là ảnh của (O) qua \({Đ_{BC}}.\)
Bài 5 trang 19 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến khảo sát hàm số. Cụ thể, bài toán yêu cầu học sinh xác định các điểm cực trị của hàm số, từ đó suy ra tính đơn điệu của hàm số trên các khoảng xác định.
Để giải bài 5 trang 19 hiệu quả, học sinh cần nắm vững các bước sau:
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Bước 1: Tính đạo hàm cấp nhất
y' = 3x2 - 6x
Bước 2: Giải phương trình y' = 03x2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
Bước 3: Xác định dấu của y'Xét các khoảng:
Tại x = 0, y' đổi dấu từ dương sang âm, nên hàm số đạt cực đại tại x = 0. Giá trị cực đại là y(0) = 2.
Tại x = 2, y' đổi dấu từ âm sang dương, nên hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là y(2) = -2.
Khi giải các bài toán về khảo sát hàm số bằng đạo hàm, học sinh cần chú ý:
Việc hiểu rõ về đạo hàm và ứng dụng của đạo hàm trong khảo sát hàm số có ý nghĩa quan trọng trong nhiều lĩnh vực của khoa học và kỹ thuật, như:
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự sau:
Bài 5 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập điển hình để rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong khảo sát hàm số. Hy vọng với lời giải chi tiết và những lưu ý quan trọng trên, các em học sinh sẽ tự tin hơn khi giải quyết các bài toán tương tự.