Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11 Chuyên đề học tập. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 4 trang 19, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, giúp bạn tự tin hơn trong quá trình học tập.
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25\) và đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25\) và đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
a) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục Ox.
b) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục Oy.
c) Tìm ảnh của (C) và \(\Delta \) qua phép đối xứng trục \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0.\)
Phương pháp giải - Xem chi tiết
Nếu \(M' = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu\(M' = {Đ_{Oy}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết
Đường tròn (C) có tâm I(3; 4), bán kính R = 5.
a)
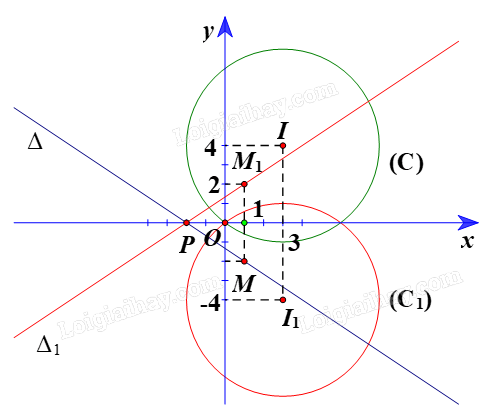
+ Gọi \(({C_1})\) là ảnh của (C) qua \({Đ_{Ox}}\), khi đó (C1) có tâm I1 là ảnh của I(3; 4) \({Đ_{Ox}}\) và bán kính \({R_1}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_1}\; = {\rm{ }}{Đ_{Ox}}\left( I \right).\)
Suy ra Ox là đường trung trực của đoạn \(\;I{I_1}\)
Do đó hai điểm I(3; 4) và I1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ \({I_1}\left( {3;{\rm{ }}-4} \right).\)
Vậy ảnh của đường tròn (C) qua ĐOx là đường tròn (C1) có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}4} \right)^2}\; = {\rm{ }}25.\)
+ Trục \(Ox:{\rm{ }}y{\rm{ }} = {\rm{ }}0.\)
Với y = 0, ta có \(2x{\rm{ }} + {\rm{ }}3.0{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} = {\rm{ }}-2.\)
Suy ra giao điểm của ∆ và trục Ox là điểm \(P\left( {-2;{\rm{ }}0} \right).\)
Khi đó \(P{\rm{ }} = {\rm{ }}{Đ_{Ox}}\left( P \right).\)
Chọn \(M\left( {1;{\rm{ }}-2} \right) \in \Delta \)
Gọi M1 và ∆1 theo thứ tự là ảnh của M và \(\Delta \) qua \({Đ_{Ox}}\)
Ta thấy Ox là đường trung trực của đoạn MM1.
Do đó hai điểm M(1; –2) và M1 có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ \({M_1}\left( {1;{\rm{ }}2} \right).\)
Ta có \(\overrightarrow {{M_1}P} = \left( { - 3; - 2} \right)\)
Đường thẳng \({\Delta _1}\;\) có vectơ chỉ phương \(\overrightarrow {{M_1}P} = \left( { - 3; - 2} \right)\)
Suy ra \({\Delta _1}\;\) có vectơ pháp tuyến \({\vec n_{{\Delta _1}}} = \left( {2; - 3} \right)\)
Vậy đường thẳng \({\Delta _1}\;\) đi qua P(–2; 0) và có vectơ pháp tuyến \({\vec n_{{\Delta _1}}} = \left( {2; - 3} \right)\) nên có phương trình là:
\(2\left( {x{\rm{ }} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }}-{\rm{ }}0} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 2x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
b)
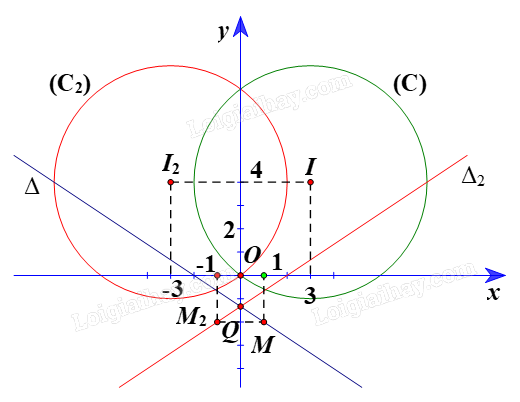
+ Gọi \(({C_2})\) là ảnh của (C) qua \({Đ_{Oy}}\), khi đó \(({C_2})\) có tâm \({I_{2\;}}\) là ảnh của \(I\left( {3;{\rm{ }}4} \right)\)qua \({Đ_{Oy}}\) và bán kính \({R_2}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_2}\; = {\rm{ }}{Đ_{Oy}}\left( I \right).\)
Suy ra Oy là đường trung trực của đoạn \(I{I_2}.\)
Do đó hai điểm I(3; 4) và \({I_{2\;}}\) có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ \({I_2}\left( {-3;{\rm{ }}4} \right).\)
Vậy ảnh của đường tròn (C) qua \({Đ_{Oy}}\) là đường tròn \(({C_2})\) có phương trình là:
\({\left( {x{\rm{ }} + {\rm{ }}3} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}4} \right)^2}\; = {\rm{ }}25.\)
+ Trục \(Oy:{\rm{ }}x{\rm{ }} = {\rm{ }}0.\)
Với x = 0, ta có \(2.0{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0{\rm{ }} \Leftrightarrow y = - \frac{4}{3}\)
Suy ra giao điểm của \(\Delta \) và trục Oy là điểm \(Q\left( {0; - \frac{4}{3}} \right)\)
Khi đó \(Q{\rm{ }} = {\rm{ }}{Đ_{Oy}}\left( Q \right).\)
Chọn \(M\left( {1;{\rm{ }}-2} \right) \in \Delta \)
Gọi \({M_2}\;\) và \({\Delta _2}\;\) theo thứ tự là ảnh của M và \(\Delta \) qua \({Đ_{Oy}}\)
Ta thấy Oy là đường trung trực của đoạn \(M{M_2}.\)
Do đó hai điểm M(1; –2) và M2 có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ \({M_2}\left( {-1;{\rm{ }}-2} \right).\)
Ta có \(\overrightarrow {{M_2}Q} = \left( {1;\frac{2}{3}} \right)\)
Đường thẳng ∆2 có vectơ chỉ phương \({\vec u_2} = 3\overrightarrow {{M_2}Q} = \left( {3;2} \right)\)
Suy ra ∆2 có vectơ pháp tuyến \({\vec n_{{\Delta _2}}} = \left( {2; - 3} \right)\)
Vậy đường thẳng \({\Delta _2}\) đi qua \({M_2}\left( {-1;{\rm{ }}-2} \right)\) và có vectơ pháp tuyến \({\vec n_{{\Delta _2}}} = \left( {2; - 3} \right)\) nên có phương trình là:
\(2\left( {x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 2x{\rm{ }}-{\rm{ }}3y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
c)
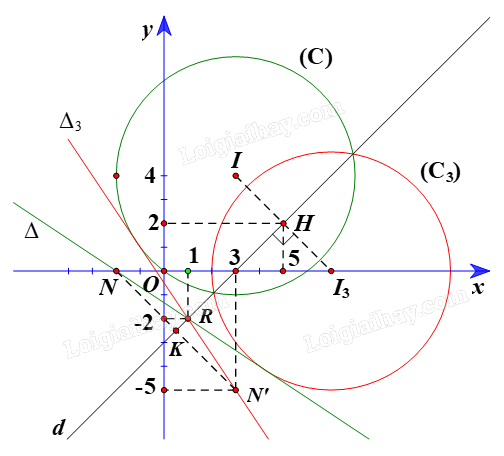
+ Gọi \({\rm{ }}({C_3})\) là ảnh của (C) qua \({Đ_d}\), khi đó \(({C_2})\) có tâm \({I_3}\) là ảnh của I(3; 4) qua Đd và bán kính \({R_3}\; = {\rm{ }}R{\rm{ }} = {\rm{ }}5.\)
Ta có \({I_3}\; = {\rm{ }}{Đ_d}\left( I \right).\)
Suy ra d là đường trung trực của đoạn II3 nên II3 ⊥ d tại trung điểm của II3.
Mà đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 1} \right)\)
Suy ra đường thẳng II3 có vectơ chỉ phương \({\vec n_d} = \left( {1; - 1} \right)\)
Do đó đường thẳng II3 có vectơ pháp tuyến \(\vec u = \left( {1;1} \right)\)
Vì vậy đường thẳng II3 đi qua điểm I(3; 4) và nhận \(\vec u = \left( {1;1} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}3} \right){\rm{ }} + {\rm{ }}1\left( {y{\rm{ }}-{\rm{ }}4} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\)
Gọi H là giao điểm của \(I{I_3}\) và đường thẳng d.
Suy ra tọa độ H thỏa mãn hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{{\rm{x}} - {\rm{y}} - 3 = 0}\\{{\rm{x}} + {\rm{y}} - 7 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = 5}\\{{\rm{y}} = 2}\end{array}} \right.\)
Do đó tọa độ \(H\left( {5;{\rm{ }}2} \right).\)
Ta có H là trung điểm \(I{I_3}.\)
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_{{{\rm{I}}_3}}} = 2{{\rm{x}}_{\rm{H}}} - {{\rm{x}}_{\rm{I}}} = 2.5 - 3 = 7}\\{{{\rm{y}}_{{{\rm{I}}_3}}} = 2{{\rm{y}}_{\rm{H}}} - {{\rm{y}}_{\rm{I}}} = 2.2 - 4 = 0}\end{array}} \right.\)
Do đó tọa độ \({I_3}\left( {7;{\rm{ }}0} \right).\)
Vậy ảnh của đường tròn (C) qua \({Đ_d}\) là đường tròn \(({C_3})\) có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}7} \right)^2}\; + {\rm{ }}{y^2}\; = {\rm{ }}25.\)
+ Gọi R là giao điểm của \(\Delta \) và d.
Suy ra tọa độ R thỏa mãn hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 3{\rm{y}} + 4 = 0}\\{{\rm{x}} - {\rm{y}} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = 1}\\{{\rm{y}} = - 2}\end{array}} \right.\)
Do đó tọa độ R(1; –2).
Khi đó \(R{\rm{ }} = {\rm{ }}{Đ_d}\left( R \right).\)
Chọn \(N\left( {-2;{\rm{ }}0} \right) \in \Delta :{\rm{ }}2x{\rm{ }} + {\rm{ }}3y{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}0.\)
Gọi N’ và \({\Delta _3}\) theo thứ tự là ảnh của N và \(\Delta \) qua \({Đ_d}\).
Ta thấy d là đường trung trực của đoạn NN’.
Mà đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 1} \right)\)
Suy ra đường thẳng NN’ có vectơ chỉ phương \({\vec n_d} = \left( {1; - 1} \right)\)
Do đó đường thẳng NN’ có vectơ pháp tuyến \(\vec u = \left( {1;1} \right)\)
Vì vậy đường thẳng NN’ đi qua N(–2; 0) và nhận \(\vec u = \left( {1;1} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} + {\rm{ }}1\left( {y{\rm{ }}-{\rm{ }}0} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}0.\)
Gọi K là giao điểm của NN’ và đường thẳng d.
Suy ra tọa độ K thỏa mãn hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{{\rm{x}} + {\rm{y}} + 2 = 0}\\{{\rm{x}} - {\rm{y}} - 3 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{x}} = \frac{1}{2}}\\{{\rm{y}} = - \frac{5}{2}}\end{array}} \right.\)
Do đó tọa độ \(K\left( {\frac{1}{2}; - \frac{5}{2}} \right)\)
Ta có K là trung điểm NN’.
Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_{{\rm{N'}}}} = 2{{\rm{x}}_{\rm{K}}} - {{\rm{x}}_{\rm{N}}} = 2.\frac{1}{2} + 2 = 3}\\{{{\rm{y}}_{{\rm{N'}}}} = 2{{\rm{y}}_{\rm{K}}} - {{\rm{y}}_{\rm{N}}} = 2.\left( { - \frac{5}{2}} \right) - 0 = - 5}\end{array}} \right.\)
Do đó tọa độ N’(3; –5).
Với R(1; –2), ta có \(\overrightarrow {N'R} = \left( { - 2;3} \right)\)
Đường thẳng \({\Delta _3}\) có vectơ chỉ phương \(\overrightarrow {N'R} = \left( { - 2;3} \right)\)
Suy ra \({\Delta _3}\) có vectơ pháp tuyến \({\vec n_{{\Delta _3}}} = \left( {3;2} \right)\)
Vậy đường thẳng \({\Delta _3}\) đi qua N’(3; –5) và nhận \({\vec n_{{\Delta _3}}} = \left( {3;2} \right)\) làm vectơ pháp tuyến nên có phương trình là:
\(3\left( {x{\rm{ }}-{\rm{ }}3} \right){\rm{ }} + {\rm{ }}2\left( {y{\rm{ }} + {\rm{ }}5} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow 3x{\rm{ }} + {\rm{ }}2y{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0.\)
Bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài, xác định rõ yêu cầu và các thông tin đã cho. Sau đó, cần lựa chọn phương pháp giải phù hợp với từng dạng bài. Đối với bài 4 trang 19, các phương pháp thường được sử dụng bao gồm:
Để giúp bạn hiểu rõ hơn về cách giải bài 4 trang 19, chúng tôi sẽ trình bày lời giải chi tiết từng bước như sau:
...
...
...
Để củng cố kiến thức và kỹ năng giải bài tập, chúng ta hãy xem xét một số ví dụ minh họa và bài tập tương tự:
Ví dụ 1: Giải bài tập tương tự với hàm số khác...
Bài tập 1: Giải bài tập tương tự với các thông số khác...
Khi giải bài tập về hàm số, đồ thị hàm số, bạn cần lưu ý một số điểm sau:
Bài 4 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp bạn rèn luyện kỹ năng phân tích hàm số, vẽ đồ thị hàm số và áp dụng các phép biến đổi hàm số. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.
| Công thức | Mô tả |
|---|---|
| y = f(x) | Hàm số y = f(x) |
| Đạo hàm f'(x) | Tính chất đơn điệu của hàm số |
| Điểm cực trị | Xác định cực đại, cực tiểu |