Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn là địa chỉ tin cậy dành cho các em học sinh muốn tìm kiếm lời giải bài tập Toán nhanh chóng và chính xác.
Cho đồ thị có trọng số như Hình 16.
Đề bài
Cho đồ thị có trọng số như Hình 16.
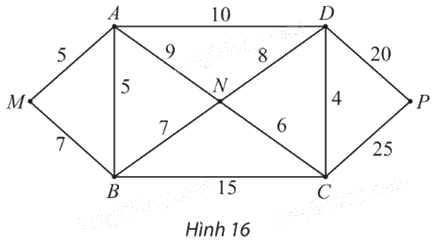
a) Tính độ dài các đường đi ABCD, MBNCP.
b) Chỉ ra ba đường đi khác nhau từ M đến N và tính độ dài của chúng.
c) MBC có phải là đường đi ngắn nhất từ M đến C không?
Phương pháp giải - Xem chi tiết
Nếu mỗi cạnh của đồ thị G được gắn với một số thực (có thể là độ dài của đường đi trên mỗi cạnh, chi phí vận chuyển trên mỗi cạnh đó,…) thì đồ thị G được gọi là đồ thị có trọng số. Trọng số của cạnh a kí hiệu là \({w_a}\)
Tổng trọng số (hay độ dài) của các cạnh tạo thành đường đi gọi là độ dài của đường đi đó. Độ dài đường đi m kí hiệu là \({l_m}\). Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh B gọi là đường đi ngắn nhất từ A đến B.
Lời giải chi tiết
a) Ta có:
\(\begin{array}{*{20}{l}}{{l_{ABCD}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CD}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}15{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}24.}\\{{l_{MBNCP}}\; = {\rm{ }}{w_{MB}}\; + {\rm{ }}{w_{BN}}\; + {\rm{ }}{w_{NC}}\; + {\rm{ }}{w_{CP}}\; = {\rm{ }}7{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}25{\rm{ }} = {\rm{ }}45.}\end{array}\)
Vậy độ dài các đường đi ABCD, MBNCP lần lượt là 24 và 45.
b) Ba đường đi khác nhau từ M đến N là: MAN, MBN, MABN.
Ta có:
\(\begin{array}{*{20}{l}}{{l_{MAN}}\; = {\rm{ }}{w_{MA}}\; + {\rm{ }}{w_{AN}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}9{\rm{ }} = {\rm{ }}14.}\\{{l_{MBN}}\; = {\rm{ }}{w_{MB}}\; + {\rm{ }}{w_{BN}}\; = {\rm{ }}7{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}14.}\\{{l_{MABN}}\; = {\rm{ }}{w_{MA}}\; + {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BN}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}5{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}17.}\end{array}\)
Vậy ba đường đi khác nhau từ M đến N là MAN, MBN, MABN có độ dài lần lượt bằng 14; 14; 17.
c) Ta có MANC là một đường đi từ M đến C.
M \({l_{MANC}}\; = {\rm{ }}{w_{MA}}\; + {\rm{ }}{w_{AN}}\; + {\rm{ }}{w_{NC}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}9{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}20,{\rm{ }}{l_{MBC}}\; = {\rm{ }}{w_{MB}}\; + {\rm{ }}{w_{BC}}\; = {\rm{ }}7{\rm{ }} + {\rm{ }}15{\rm{ }} = {\rm{ }}22.\)
Vì 20 < 22 nên \({l_{MANC}}\; < {\rm{ }}{l_{MBC}}.\)
Vậy MBC không phải là đường đi ngắn nhất từ M đến C.
Bài 1 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải có sự hiểu biết sâu sắc về lý thuyết và khả năng áp dụng linh hoạt các công thức, định lý đã học.
Bài 1 trang 66 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Bài tập: Xét hàm số y = x2 - 4x + 3. Tìm tập xác định và tập giá trị của hàm số.
Giải:
Khi giải bài 1 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo, học sinh cần lưu ý:
Bài 1 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và rèn luyện kỹ năng giải bài tập. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả đã được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định tập xác định | Xét điều kiện để hàm số có nghĩa |
| Tìm tập giá trị | Tìm giá trị lớn nhất, nhỏ nhất của hàm số |
| Khảo sát sự biến thiên | Tính đạo hàm, xét dấu đạo hàm |