Bài khởi động trang 6 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo là phần mở đầu quan trọng, giúp học sinh ôn lại kiến thức cũ và làm quen với nội dung mới của chương. giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự tin giải quyết bài tập và nắm vững kiến thức.
: Bức tranh trang trí trong hình bên trước khi tô màu thực chất được tạo ra từ một hình mũi tên duy nhất và được dời chỗ tới các vị trí khác nhau.
Đề bài
Bức tranh trang trí trong hình bên trước khi tô màu thực chất được tạo ra từ một hình mũi tên duy nhất và được dời chỗ tới các vị trí khác nhau. Hãy thảo luận để tìm hiểu về các phép biến đổi hình học nào đã tạo ra tất cả các hình mũi tên như vậy từ một hình mũi tên ban đầu.
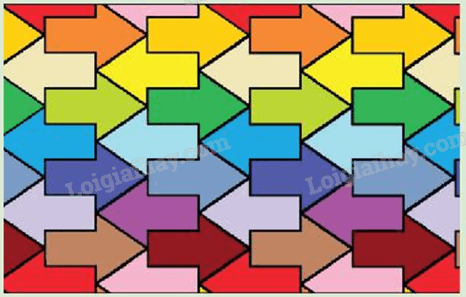
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ để trả lời
Lời giải chi tiết
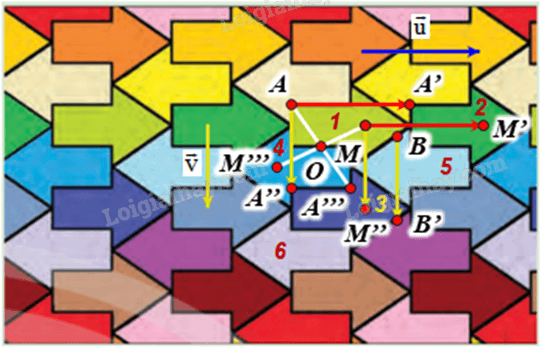
Giả sử mũi tên ban đầu là mũi tên đánh số 1.
+ Gọi A là một điểm trên hình mũi tên 1 và \(\vec u\) có phương song song với trục đối xứng của hình mũi tên 1, độ dài của \(\vec u\) bằng độ dài từ điểm đầu tới điểm cuối của mũi tên 1 (hình vẽ).
Lấy điểm A’ sao cho \(\overrightarrow {AA'} = \vec u\)
Khi đó điểm A’ là một điểm trên hình mũi tên 2 có vị trí tương ứng với điểm A trên hình mũi tên 1.
Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’ sao cho \(\overrightarrow {MM'} = \vec u\) thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’ tạo thành hình mũi tên 2.
+ Gọi A’’ là một điểm trên hình mũi tên 3 có vị trí tương ứng với điểm A trên hình mũi tên 1.
Giả sử \(\vec v\) là vectơ có phương vuông góc với trục đối xứng của hình mũi tên 1, độ dài bằng độ dài từ điểm A đến điểm A’’ (hình vẽ).
Tức là, \(\vec v = \overrightarrow {AA''} \).
Gọi B là một điểm trên hình mũi tên 1.
Lấy điểm B’ sao cho \(\overrightarrow {BB'} = \vec v\).
Khi đó điểm B’ là một điểm trên hình mũi tên 3 có vị trí tương ứng với điểm B trên hình mũi tên 1.
Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’’ sao cho \(\overrightarrow {MM''} = \vec v\) thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’’ tạo thành hình mũi tên 3.
+ Gọi O là một điểm trên hình mũi tên 1 (hình vẽ).
Lấy điểm A’’’ đối xứng với A qua O.
Khi đó điểm A’’’ là một điểm trên hình mũi tên 4 có vị trí tương ứng với điểm A trên hình mũi tên 1.
Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’’’ đối xứng với M qua O thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’’’ tạo thành hình mũi tên 4.
+ Tương tự trường hợp chứng minh từ hình mũi tên 1 thành hình mũi tên 2, ta chứng minh được trường hợp từ hình mũi tên 4 thành hình mũi tên 5.
+ Tương tự trường hợp chứng minh từ hình mũi tên 1 thành hình mũi tên 3, ta chứng minh được trường hợp từ hình mũi tên 4 thành hình mũi tên 6.
+ Tương tự như vậy với tất cả các hình mũi tên khác.
Vậy hai phép biến đổi hình học cần tìm là phép biến đổi theo vectơ \(\vec u\) có phương song song với trục đối xứng, độ dài bằng độ dài từ điểm đầu tới điểm cuối của mũi tên ban đầu và phép biến đổi lấy điểm đối xứng qua một điểm.
Bài khởi động trang 6 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo đóng vai trò quan trọng trong việc giúp học sinh ôn lại kiến thức nền tảng và chuẩn bị cho các nội dung mới của chương. Bài tập này thường mang tính chất gợi mở, kích thích tư duy và khả năng vận dụng kiến thức vào thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, phân tích phương pháp giải và những lưu ý quan trọng để học sinh có thể tự tin chinh phục bài tập này.
Bài khởi động trang 6 thường xoay quanh các kiến thức đã học ở chương trình Toán 10, đặc biệt là các kiến thức về vectơ, hình học phẳng và các phép biến hình. Mục đích của bài tập là giúp học sinh:
Để giải bài khởi động trang 6, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho bài khởi động trang 6 (ví dụ, giả sử bài tập yêu cầu tìm tọa độ điểm D sao cho ABCD là hình bình hành):
Bước 1: Xác định các vectơ liên quan. Ví dụ, vectơ AB và vectơ DC.
Bước 2: Áp dụng tính chất của hình bình hành: AB = DC.
Bước 3: Sử dụng tọa độ của các điểm A, B, C để tìm tọa độ của điểm D.
Để giải các bài tập liên quan đến vectơ và hình học phẳng, học sinh có thể áp dụng các phương pháp sau:
Khi giải bài tập vectơ và hình học phẳng, học sinh cần lưu ý những điều sau:
Kiến thức về vectơ và hình học phẳng có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo các bài tập sau:
Bài khởi động trang 6 Chuyên đề học tập Toán 11 - Chân trời sáng tạo là cơ hội tốt để học sinh ôn lại kiến thức cũ và chuẩn bị cho các nội dung mới. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các phương pháp giải phù hợp và rèn luyện kỹ năng thường xuyên, học sinh có thể tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.