Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 12, 13 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Chúng tôi cung cấp các bước giải bài tập rõ ràng, kèm theo giải thích chi tiết để các em có thể tự học và hiểu sâu sắc vấn đề.
Cho vectơ \(\overrightarrow u \) và đường thẳng d. A và M là hai điểm bất kì trên d. Gọi A’ và M’ lần lượt là ảnh của A và M qua phép tịnh tiến \({{\rm{T}}_{{\rm{\vec u}}}}\).
Trong mặt phẳng tọa độ Oxy, xét phép tịnh tiến \({T_{\overrightarrow v }}\) với \(\overrightarrow v = (3;2).\)
a) Biết ảnh của điểm M qua \({T_{\overrightarrow v }}\) là điểm M’(–8; 5). Tìm tọa độ điểm M.
b) Tìm ảnh của đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}3} \right)^2}\; = {\rm{ }}4{\rm{ }}\)qua \({T_{\overrightarrow v }}\).
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Lời giải chi tiết:
a) Đặt \(\;M\left( {x;{\rm{ }}y} \right).\)Suy ra \(\;\overrightarrow {MM'} = ( - 8 - x;5 - y).\)
Theo đề, ta có \(M' = {T_{\overrightarrow v }}(M)\;.\).
Suy ra \(\overrightarrow {MM'} = \overrightarrow v .\).
Khi đó \(\left\{ \begin{array}{l} - 8 - x = 3\\5 - y = 2\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}\;x = - 11\\y = 3\end{array} \right.\)
Vậy tọa độ M(–11; 3) thỏa mãn yêu cầu bài toán.
b) Đường tròn (C) có tâm I(2; –3), bán kính R = 4.
Gọi (C’), I’(x’; y’) lần lượt là ảnh của (C) và I qua \({T_{\overrightarrow v }}\).
Khi đó đường tròn (C’) có bán kính \(R'{\rm{ }} = {\rm{ }}R{\rm{ }} = {\rm{ }}2\) và \(\overrightarrow {II'} = (x' - 2;y' + 3)\)
Ta có \(\;\overrightarrow {II'} = \overrightarrow {v\;} \) (vì \(I' = {T_{\overrightarrow v }}(I)\))
Suy ra \(\left\{ \begin{array}{l}x' - 2 = 3\\y' + 3 = 2\end{array} \right.\)
Do đó \(\left\{ \begin{array}{l}x' = 5\\y' = - 1\end{array} \right.\)
Suy ra tọa độ tâm đường tròn (C’) là \(I'\left( {5;{\rm{ }}-1} \right).\)
Vậy ảnh của đường tròn (C) là đường tròn (C’) có phương trình là: \({\left( {x{\rm{ }}-{\rm{ }}5} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\)
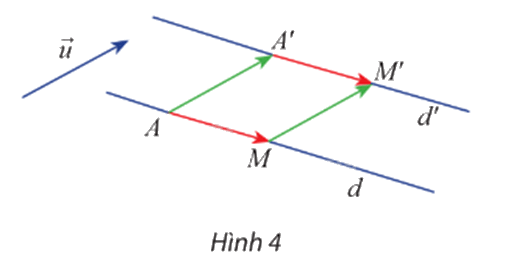
Cho vectơ \(\overrightarrow u \) và đường thẳng d. A và M là hai điểm bất kì trên d. Gọi A’ và M’ lần lượt là ảnh của A và M qua phép tịnh tiến \({{\rm{T}}_{{\rm{\vec u}}}}\).
a) Hai vectơ ‘ có bằng nhau không?
b) Khi điểm M thay đổi trên d thì điểm M’ thay đổi như thế nào? Giải thích.
Phương pháp giải:
Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải chi tiết:
a) Ta có \({{\rm{T}}_{{\rm{\vec u}}}}\left( {\rm{A}} \right) = {\rm{A'}}\), suy ra \(\overrightarrow {AA'} = {\rm{\vec u}}\).
\({{\rm{T}}_{{\rm{\vec u}}}}\left( {\rm{M}} \right) = {\rm{M'}}\), suy ra \(\overrightarrow {MM'} = {\rm{\vec u}}\).
Khi đó \(\overrightarrow {AA'} = \overrightarrow {MM'} \,\,\,\left( { = {\rm{\vec u}}} \right)\).
Suy ra AA’ = MM’ và AA’ // MM’.
Vì vậy tứ giác AMM’A’ là hình bình hành.
Vậy \(\overrightarrow {{\rm{A'M'}}} = \overrightarrow {AM} \).
b) Gọi d’ là giá của \(\overrightarrow {{\rm{A'M'}}} \).
Vì A’M’ // AM (do tứ giác AMM’A’ là hình bình hành).
Nên d’ // d.
Vậy khi điểm M thay đổi trên d thì điểm M’ thay đổi trên d’ thỏa mãn \(\overrightarrow {MM'} = {\rm{\vec u}}\).
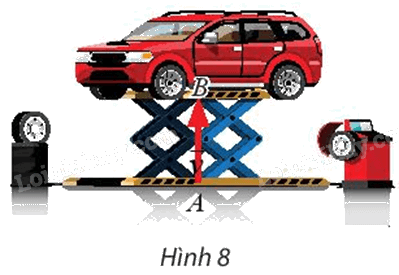
Cho vectơ \(\overrightarrow u \) và đường thẳng d. A và M là hai điểm bất kì trên d. Gọi A’ và M’ lần lượt là ảnh của A và M qua phép tịnh tiến \({{\rm{T}}_{{\rm{\vec u}}}}\).
a) Hai vectơ ‘ có bằng nhau không?
b) Khi điểm M thay đổi trên d thì điểm M’ thay đổi như thế nào? Giải thích.
Phương pháp giải:
Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải chi tiết:
a) Ta có \({{\rm{T}}_{{\rm{\vec u}}}}\left( {\rm{A}} \right) = {\rm{A'}}\), suy ra \(\overrightarrow {AA'} = {\rm{\vec u}}\).
\({{\rm{T}}_{{\rm{\vec u}}}}\left( {\rm{M}} \right) = {\rm{M'}}\), suy ra \(\overrightarrow {MM'} = {\rm{\vec u}}\).
Khi đó \(\overrightarrow {AA'} = \overrightarrow {MM'} \,\,\,\left( { = {\rm{\vec u}}} \right)\).
Suy ra AA’ = MM’ và AA’ // MM’.
Vì vậy tứ giác AMM’A’ là hình bình hành.
Vậy \(\overrightarrow {{\rm{A'M'}}} = \overrightarrow {AM} \).
b) Gọi d’ là giá của \(\overrightarrow {{\rm{A'M'}}} \).
Vì A’M’ // AM (do tứ giác AMM’A’ là hình bình hành).
Nên d’ // d.
Vậy khi điểm M thay đổi trên d thì điểm M’ thay đổi trên d’ thỏa mãn \(\overrightarrow {MM'} = {\rm{\vec u}}\).
Trong mặt phẳng tọa độ Oxy, xét phép tịnh tiến \({T_{\overrightarrow v }}\) với \(\overrightarrow v = (3;2).\)
a) Biết ảnh của điểm M qua \({T_{\overrightarrow v }}\) là điểm M’(–8; 5). Tìm tọa độ điểm M.
b) Tìm ảnh của đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}3} \right)^2}\; = {\rm{ }}4{\rm{ }}\)qua \({T_{\overrightarrow v }}\).
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Lời giải chi tiết:
a) Đặt \(\;M\left( {x;{\rm{ }}y} \right).\)Suy ra \(\;\overrightarrow {MM'} = ( - 8 - x;5 - y).\)
Theo đề, ta có \(M' = {T_{\overrightarrow v }}(M)\;.\).
Suy ra \(\overrightarrow {MM'} = \overrightarrow v .\).
Khi đó \(\left\{ \begin{array}{l} - 8 - x = 3\\5 - y = 2\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}\;x = - 11\\y = 3\end{array} \right.\)
Vậy tọa độ M(–11; 3) thỏa mãn yêu cầu bài toán.
b) Đường tròn (C) có tâm I(2; –3), bán kính R = 4.
Gọi (C’), I’(x’; y’) lần lượt là ảnh của (C) và I qua \({T_{\overrightarrow v }}\).
Khi đó đường tròn (C’) có bán kính \(R'{\rm{ }} = {\rm{ }}R{\rm{ }} = {\rm{ }}2\) và \(\overrightarrow {II'} = (x' - 2;y' + 3)\)
Ta có \(\;\overrightarrow {II'} = \overrightarrow {v\;} \) (vì \(I' = {T_{\overrightarrow v }}(I)\))
Suy ra \(\left\{ \begin{array}{l}x' - 2 = 3\\y' + 3 = 2\end{array} \right.\)
Do đó \(\left\{ \begin{array}{l}x' = 5\\y' = - 1\end{array} \right.\)
Suy ra tọa độ tâm đường tròn (C’) là \(I'\left( {5;{\rm{ }}-1} \right).\)
Vậy ảnh của đường tròn (C) là đường tròn (C’) có phương trình là: \({\left( {x{\rm{ }}-{\rm{ }}5} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\)
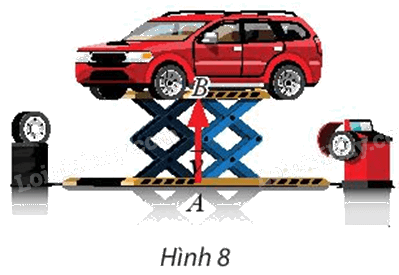
Trong Hình 8, người thợ sửa xe đã dùng kích nâng thủy lực để đưa ô tô từ mặt đất đến vị trí cần thiết thông qua phép biến hình nào?
Phương pháp giải:
Quan sát hình vẽ và suy luận để trả lời
Lời giải chi tiết:
Ta thấy ô tô được nâng từ vị trí A đến vị trí B.
Khi đó chiếc xe ô tô được tịnh tiến theo vectơ \(\vec v = \overrightarrow {AB} \) từ mặt đất lên vị trí cần thiết.
Vậy người thợ sửa xe đã dùng kích nâng thủy lực để đưa ô tô từ mặt đất đến vị trí cần thiết thông qua phép tịnh tiến theo \(\vec v = \overrightarrow {AB} \).
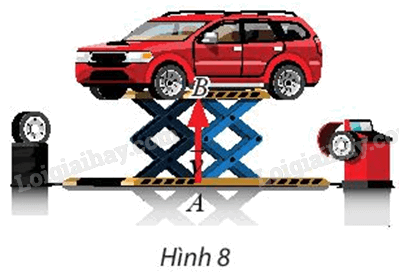
Trong Hình 8, người thợ sửa xe đã dùng kích nâng thủy lực để đưa ô tô từ mặt đất đến vị trí cần thiết thông qua phép biến hình nào?
Phương pháp giải:
Quan sát hình vẽ và suy luận để trả lời
Lời giải chi tiết:
Ta thấy ô tô được nâng từ vị trí A đến vị trí B.
Khi đó chiếc xe ô tô được tịnh tiến theo vectơ \(\vec v = \overrightarrow {AB} \) từ mặt đất lên vị trí cần thiết.
Vậy người thợ sửa xe đã dùng kích nâng thủy lực để đưa ô tô từ mặt đất đến vị trí cần thiết thông qua phép tịnh tiến theo \(\vec v = \overrightarrow {AB} \).
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là rất quan trọng để hiểu rõ hơn về các khái niệm và ứng dụng của Toán học trong thực tế.
Để giải quyết các bài tập trong mục 2 trang 12, 13, trước tiên chúng ta cần hiểu rõ các khái niệm và định lý liên quan. Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường trình bày các kiến thức một cách trực quan và dễ hiểu, nhưng việc luyện tập thường xuyên là cần thiết để nắm vững chúng.
Bài tập 1 thường yêu cầu học sinh áp dụng các kiến thức đã học để giải quyết một vấn đề cụ thể. Để giải bài tập này, chúng ta cần:
Bài tập 2 thường yêu cầu học sinh ứng dụng các kiến thức đã học để giải quyết một vấn đề thực tế. Để giải bài tập này, chúng ta cần:
Trong mục 2 trang 12, 13, học sinh có thể gặp các dạng bài tập sau:
Để giải bài tập Toán 11 hiệu quả, học sinh có thể áp dụng các mẹo sau:
Ví dụ: Giải phương trình 2x + 3 = 7
Giải:
Vậy nghiệm của phương trình là x = 2.
Để học tập và ôn luyện Toán 11 hiệu quả, học sinh có thể tham khảo các tài liệu sau:
Việc giải mục 2 trang 12, 13 Chuyên đề học tập Toán 11 - Chân trời sáng tạo đòi hỏi sự hiểu biết vững chắc về các khái niệm và kỹ năng giải bài tập. Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập một cách hiệu quả. Chúc các em học tập tốt!