Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 1 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải này một cách cẩn thận, dễ hiểu, phù hợp với trình độ của học sinh.
Sử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây:
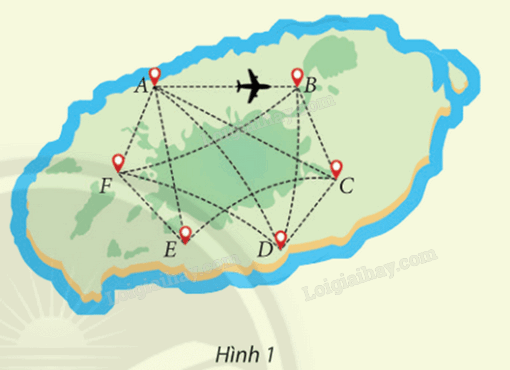
Sử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây:
a) Từ thành phố A, hãng X có bao nhiêu đường bay đến năm thành phố còn lại?
b) Giữa sáu thành phố trên, có tất cả bao nhiêu đường bay của hãng X?
c) Có thể giải đáp thắc mắc ở Hoạt động khởi động không?
Phương pháp giải:
Quan sát hình 1 để trả lời câu hỏi
Lời giải chi tiết:
a) Quan sát sơ đồ ở Hình 1, ta thấy:
⦁ Có 1 đường bay từ thành phố A đến thành phố B;
⦁ Có 1 đường bay từ thành phố A đến thành phố D;
⦁ Có 1 đường bay từ thành phố A đến thành phố E;
⦁ Có 1 đường bay từ thành phố A đến thành phố F.
Vậy từ thành phố A, hãng X có tất cả 4 đường bay đến năm thành phố còn lại.
b)Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố B đến thành phố A đã được tính vào đường bay từ thành phố A đến thành phố B.
Do đó từ thành phố B, hãng X có thêm:
⦁ 1 đường bay đến thành phố C;
⦁ 1 đường bay đến thành phố D;
⦁ 1 đường bay đến thành phố F.
Khi đó, từ thành phố B, hãng X có thêm 3 đường bay đến năm thành phố còn lại.
Tương tự như vậy, ta được:
– Từ thành phố C, hãng X có thêm 2 đường bay đến năm thành phố còn lại;
– Từ thành phố D, hãng X có thêm 1 đường bay đến năm thành phố còn lại;
– Từ thành phố E, hãng X có thêm 1 đường bay đến năm thành phố còn lại.
Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố F đến năm thành phố còn lại đã được tính vào các đường bay kể trên.
Vậy giữa sáu thành phố trên, có tất cả 4 + 3 + 2 + 1 + 1 = 11 đường bay của hãng X.
Chú ý: Ngoài cách trên, ta có thể đếm số đường cong và đường thẳng (thể hiện đường bay) trên Hình 1 (hoặc Bảng 1) để kết luận về số đường bay của hãng X.
c) Ta có thể giải đáp thắc mắc ở Hoạt động khởi động như sau:
Bước 1: Từ thành phố A bay đến thành phố B;
Bước 2: Từ thành phố B bay đến thành phố C;
Bước 3: Từ thành phố C bay đến thành phố D;
Bước 4: Từ thành phố D bay đến thành phố F;
Bước 5: Từ thành phố F bay đến thành phố E;
Bước 6: Từ thành phố E bay về thành phố A.
Vậy từ thành phố A, ta có thể thăm năm thành phố B, C, D, E và F bằng các chuyến bay của hãng X sao cho mỗi thành phố chỉ qua đúng một lần, rồi quay trở về A.
Chú ý: Ta có thể thay đổi thứ tự bay đến các thành phố chỉ cần hãng X có chuyến bay giữa hai thành phố liền kề.
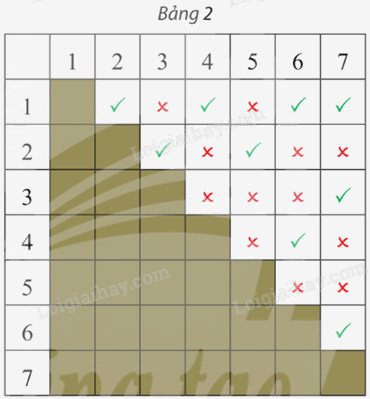
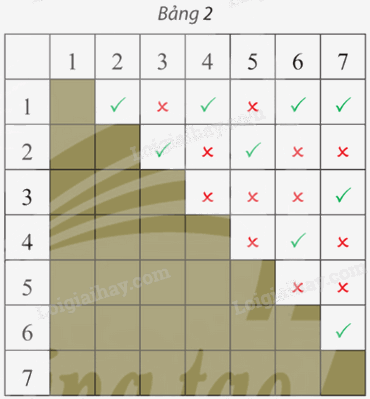
Một mạng cục bộ có bảy máy tính 1; 2; 3; 4; 5; 6 và 7. Bảng 2 cho biết giữa mỗi cặp máy tính có kết nối trực tiếp với nhau hay không (dấu ✔ là có kết nối, dấu ✘ là không kết nối). Hãy vẽ đồ thị biểu diễn sự kết nối giữa các máy tính của mạng này.
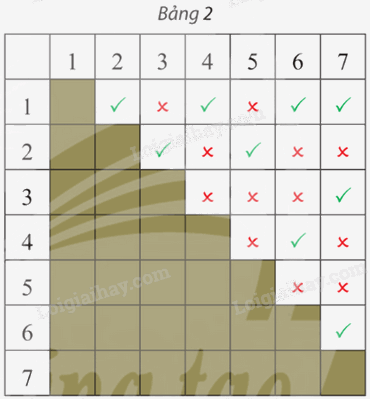
Phương pháp giải:
Dựa vào bảng 2 để vẽ đồ thị
Lời giải chi tiết:
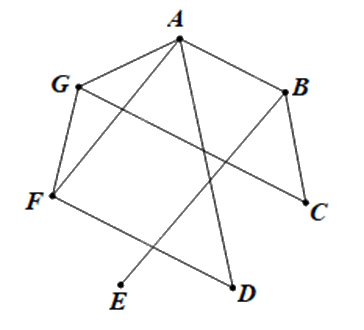
Ta vẽ đồ thị G có 7 đỉnh A, B, C, D, E, F, G lần lượt biểu diễn bảy máy tính 1; 2; 3; 4; 5; 6 và 7.
Hai đỉnh được nối bằng một cạnh nếu giữa hai máy tính có kết nối trực tiếp với nhau.
Ta có đồ thị G như sau:
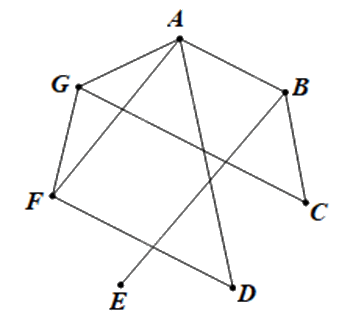
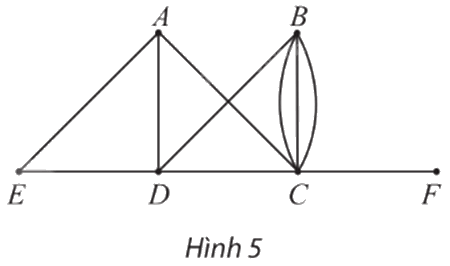
Cho đồ thị G như Hình 5.
a) Chỉ ra các đỉnh, các cạnh, số đỉnh, số cạnh của G.
b) Chỉ ra các đỉnh kề đỉnh D, các đỉnh kề đỉnh B.
c) Đồ thị G có đỉnh cô lập không?
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
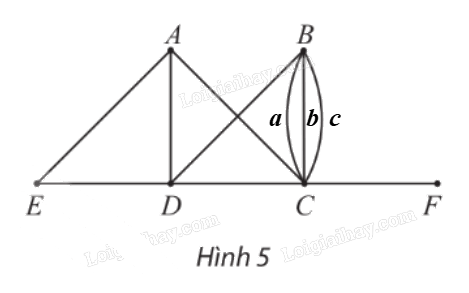
a) Các đỉnh của đồ thị G là: A, B, C, D, E và F. Đồ thị có 6 đỉnh.
Các cạnh của đồ thị G là: AC, AD, AE, a, b, c, BD, CD, CF, DE. Đồ thị có 10 cạnh.
b) Các đỉnh kề đỉnh D là: A, B, C, E.
Các đỉnh kề đỉnh B là: C, D.
c) Đồ thị G không có đỉnh cô lập.
Sử dụng sơ đồ ở Hình 1 để trả lời các câu hỏi dưới đây:
a) Từ thành phố A, hãng X có bao nhiêu đường bay đến năm thành phố còn lại?
b) Giữa sáu thành phố trên, có tất cả bao nhiêu đường bay của hãng X?
c) Có thể giải đáp thắc mắc ở Hoạt động khởi động không?
Phương pháp giải:
Quan sát hình 1 để trả lời câu hỏi
Lời giải chi tiết:
a) Quan sát sơ đồ ở Hình 1, ta thấy:
⦁ Có 1 đường bay từ thành phố A đến thành phố B;
⦁ Có 1 đường bay từ thành phố A đến thành phố D;
⦁ Có 1 đường bay từ thành phố A đến thành phố E;
⦁ Có 1 đường bay từ thành phố A đến thành phố F.
Vậy từ thành phố A, hãng X có tất cả 4 đường bay đến năm thành phố còn lại.
b)Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố B đến thành phố A đã được tính vào đường bay từ thành phố A đến thành phố B.
Do đó từ thành phố B, hãng X có thêm:
⦁ 1 đường bay đến thành phố C;
⦁ 1 đường bay đến thành phố D;
⦁ 1 đường bay đến thành phố F.
Khi đó, từ thành phố B, hãng X có thêm 3 đường bay đến năm thành phố còn lại.
Tương tự như vậy, ta được:
– Từ thành phố C, hãng X có thêm 2 đường bay đến năm thành phố còn lại;
– Từ thành phố D, hãng X có thêm 1 đường bay đến năm thành phố còn lại;
– Từ thành phố E, hãng X có thêm 1 đường bay đến năm thành phố còn lại.
Vì đường bay của hãng X là đường bay hai chiều nên đường bay từ thành phố F đến năm thành phố còn lại đã được tính vào các đường bay kể trên.
Vậy giữa sáu thành phố trên, có tất cả 4 + 3 + 2 + 1 + 1 = 11 đường bay của hãng X.
Chú ý: Ngoài cách trên, ta có thể đếm số đường cong và đường thẳng (thể hiện đường bay) trên Hình 1 (hoặc Bảng 1) để kết luận về số đường bay của hãng X.
c) Ta có thể giải đáp thắc mắc ở Hoạt động khởi động như sau:
Bước 1: Từ thành phố A bay đến thành phố B;
Bước 2: Từ thành phố B bay đến thành phố C;
Bước 3: Từ thành phố C bay đến thành phố D;
Bước 4: Từ thành phố D bay đến thành phố F;
Bước 5: Từ thành phố F bay đến thành phố E;
Bước 6: Từ thành phố E bay về thành phố A.
Vậy từ thành phố A, ta có thể thăm năm thành phố B, C, D, E và F bằng các chuyến bay của hãng X sao cho mỗi thành phố chỉ qua đúng một lần, rồi quay trở về A.
Chú ý: Ta có thể thay đổi thứ tự bay đến các thành phố chỉ cần hãng X có chuyến bay giữa hai thành phố liền kề.
Cho đồ thị G như Hình 5.
a) Chỉ ra các đỉnh, các cạnh, số đỉnh, số cạnh của G.
b) Chỉ ra các đỉnh kề đỉnh D, các đỉnh kề đỉnh B.
c) Đồ thị G có đỉnh cô lập không?
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
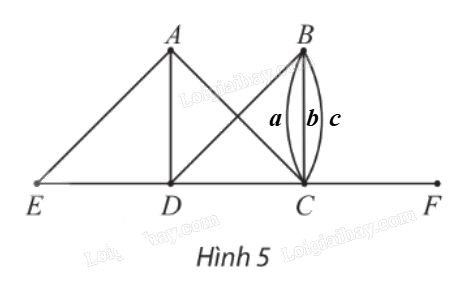
a) Các đỉnh của đồ thị G là: A, B, C, D, E và F. Đồ thị có 6 đỉnh.
Các cạnh của đồ thị G là: AC, AD, AE, a, b, c, BD, CD, CF, DE. Đồ thị có 10 cạnh.
b) Các đỉnh kề đỉnh D là: A, B, C, E.
Các đỉnh kề đỉnh B là: C, D.
c) Đồ thị G không có đỉnh cô lập.
Một mạng cục bộ có bảy máy tính 1; 2; 3; 4; 5; 6 và 7. Bảng 2 cho biết giữa mỗi cặp máy tính có kết nối trực tiếp với nhau hay không (dấu ✔ là có kết nối, dấu ✘ là không kết nối). Hãy vẽ đồ thị biểu diễn sự kết nối giữa các máy tính của mạng này.
Phương pháp giải:
Dựa vào bảng 2 để vẽ đồ thị
Lời giải chi tiết:
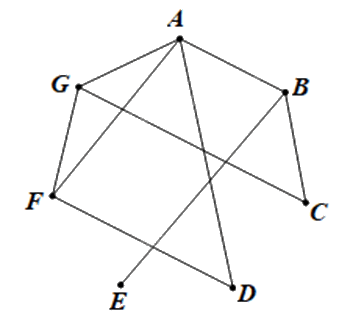
Ta vẽ đồ thị G có 7 đỉnh A, B, C, D, E, F, G lần lượt biểu diễn bảy máy tính 1; 2; 3; 4; 5; 6 và 7.
Hai đỉnh được nối bằng một cạnh nếu giữa hai máy tính có kết nối trực tiếp với nhau.
Ta có đồ thị G như sau:
Bài 1 trong Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về dãy số, giới hạn dãy số và cấp số cộng, cấp số nhân. Đây là nền tảng quan trọng cho việc học các kiến thức nâng cao hơn trong chương trình Toán 11.
Bài 1 bao gồm các dạng bài tập sau:
Đề bài: Cho dãy số (un) được xác định bởi u1 = 2 và un+1 = 2un - 1. Tính u5.
Lời giải:
Vậy u5 = 17.
Đề bài: Cho cấp số cộng (un) có u1 = 3 và công sai d = 2. Tính tổng của 10 số hạng đầu tiên của cấp số cộng.
Lời giải:
Tổng của n số hạng đầu tiên của cấp số cộng được tính theo công thức: Sn = n/2 * (2u1 + (n-1)d)
Áp dụng công thức, ta có:
S10 = 10/2 * (2(3) + (10-1)2) = 5 * (6 + 18) = 5 * 24 = 120
Vậy tổng của 10 số hạng đầu tiên của cấp số cộng là 120.
Đề bài: Chứng minh rằng dãy số (un) được xác định bởi un = n2 + 1 là dãy số tăng.
Lời giải:
Để chứng minh dãy số (un) là dãy số tăng, ta cần chứng minh un+1 > un với mọi n thuộc N*.
Ta có: un+1 = (n+1)2 + 1 = n2 + 2n + 1 + 1 = n2 + 2n + 2
Khi đó: un+1 - un = (n2 + 2n + 2) - (n2 + 1) = 2n + 1
Vì n thuộc N* nên 2n + 1 > 0. Do đó, un+1 - un > 0, suy ra un+1 > un.
Vậy dãy số (un) là dãy số tăng.
Để giải tốt các bài tập về dãy số, giới hạn dãy số và cấp số cộng, cấp số nhân, bạn cần:
Hy vọng bài giải chi tiết bài 1 trang 44, 45, 46 Chuyên đề học tập Toán 11 Chân trời sáng tạo này sẽ giúp bạn hiểu rõ hơn về các kiến thức về dãy số và tự tin giải các bài tập tương tự. Chúc bạn học tập tốt!