Bài 5 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 80, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài.
Dùng giấy kẻ ô li với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm
Đề bài
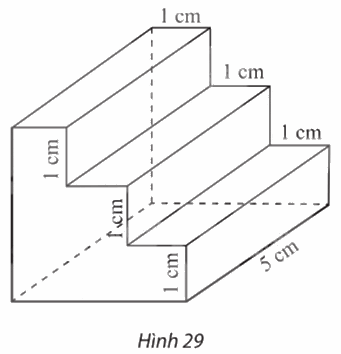
Dùng giấy kẻ ô li với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm, vẽ hình biểu diễn của chi tiết cơ khí có hình dạng và các kích thước như trong Hình 29.
Phương pháp giải - Xem chi tiết
Dựa vào hình 29 để vẽ
Lời giải chi tiết
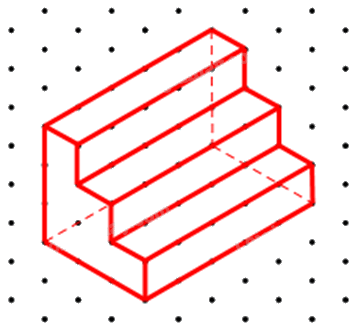
Hình biểu diễn của chi tiết cơ khí có hình dạng và các kích thước như trong Hình 29 là:
Bài 5 trang 80 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến sự biến thiên của hàm số. Cụ thể, bài toán yêu cầu học sinh xác định khoảng đơn điệu của hàm số, tìm cực trị và vẽ đồ thị hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý về đạo hàm, bao gồm đạo hàm của hàm số, điều kiện cần và đủ để hàm số đơn điệu, điều kiện để hàm số đạt cực trị.
Trước khi bắt đầu giải bài toán, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu và các dữ kiện đã cho. Sau đó, học sinh cần xác định phương pháp giải phù hợp. Trong trường hợp bài 5 trang 80, phương pháp giải chính là sử dụng đạo hàm để xét sự biến thiên của hàm số. Cụ thể, các bước giải như sau:
Để minh họa phương pháp giải, chúng ta sẽ cùng nhau giải bài 5 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo. (Giả sử đề bài cụ thể là: Xét hàm số f(x) = x3 - 3x2 + 2. Tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.)
f'(x) = 3x2 - 6x
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
| Khoảng | x < 0 | 0 < x < 2 | x > 2 |
|---|---|---|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
f''(x) = 6x - 6
f''(0) = -6 < 0 ⇒ Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2
f''(2) = 6 > 0 ⇒ Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2
Hàm số f(x) = x3 - 3x2 + 2 đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Đạo hàm không chỉ là một công cụ quan trọng trong toán học mà còn có nhiều ứng dụng trong thực tế, như:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài 5 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo và các bài tập tương tự. Chúc các em học tốt!