Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 6 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập, đáp án chính xác và giải thích rõ ràng từng bước để giúp học sinh hiểu sâu kiến thức.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O với góc quay 45°?
Đề bài
Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O với góc quay 45°?
A. \(M'\left( {1;{\rm{ }}1} \right).\)
B. \(M'\left( {1;{\rm{ }}0} \right).\)
C. \(M'\left( {\sqrt 2 ;0} \right)\)
D. \(M'\left( {0;\sqrt 2 } \right)\)
Phương pháp giải - Xem chi tiết
Phép quay tâm O, góc quay \(\alpha \) : \({Q_{(O,\alpha )\;}}{\rm{[}}M\left( {x;y} \right)]{\rm{ }} = {\rm{ }}M'\left( {x';y'} \right).\;\)
Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Lời giải chi tiết
Đáp án đúng là: D
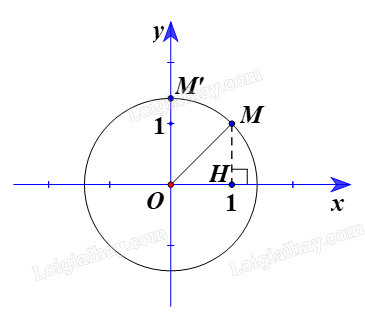
Ta có \(\overrightarrow {OM} = \left( {1;1} \right)\). Suy ra \(OM = \sqrt 2 \)
Vẽ đường tròn (C) tâm O, bán kính OM.
Ta có \({Q_{(O,{\rm{ }}45^\circ )}}\) biến điểm M khác O thành điểm M’ sao cho \(OM' = OM = \sqrt 2 \) và \(\left( {OM',{\rm{ }}OM} \right){\rm{ }} = {\rm{ }}45^\circ \;\) hay \(\widehat {MOM'} = 45^\circ \)
Kẻ \(MH \bot Ox\) tại H.
\(\Delta \) OMH vuông tại H: \(\cos \widehat {MOH} = \frac{{OH}}{{OM}} = \frac{1}{{\sqrt 2 }}\)
Suy ra \(\widehat {MOH} = 45^\circ \)
Ta có \(\widehat {HOM'} = \widehat {HOM} + \widehat {MOM'} = 45^\circ + 45^\circ = 90^\circ \)
Suy ra \(M' \in Oy\) nên \({x_{M'}}\; = {\rm{ }}0.\)
Mà \(OM' = \sqrt 2 \) (chứng minh trên) nên \({y_{M'}} = \sqrt 2 \)
Vậy tọa độ \(M'\left( {0;\sqrt 2 } \right)\)
Do đó ta chọn phương án D.
Bài 6 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải bài 6 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2.
Bước 1: Hàm số f(x) = x3 - 3x2 + 2.
Bước 2: Đạo hàm cấp nhất: f'(x) = 3x2 - 6x.
Bước 3: Tìm điểm dừng: f'(x) = 0 => 3x2 - 6x = 0 => x = 0 hoặc x = 2.
Bước 4: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Bước 5: Kết luận: Hàm số f(x) đồng biến trên khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2). Hàm số đạt cực đại tại x = 0 với giá trị f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị f(2) = -2.
Để học tập và ôn luyện hiệu quả, bạn có thể tham khảo các tài liệu sau:
Bài 6 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.