Bài tập khởi động trang 14 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo là cơ hội để học sinh ôn lại kiến thức cũ và làm quen với những khái niệm mới. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Trong các hình sau, hình nào có trục đối xứng?
Đề bài
Trong các hình sau, hình nào có trục đối xứng?
Có phép biến hình nào biến một nửa mỗi hình phẳng sau đây thành nửa còn lại không?

Phương pháp giải - Xem chi tiết
Quan sát hình vẽ, suy luận để trả lời
Lời giải chi tiết
+ Trong các hình đã cho, cả ba hình đều có trục đối xứng là đường thẳng màu vàng ở mỗi hình.
+ Ta xét hình chiếc lá:
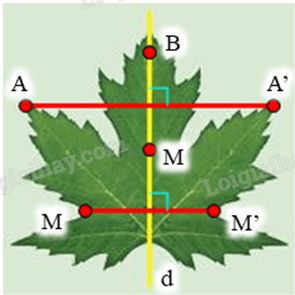
Lấy điểm A bất kì trên chiếc lá sao cho A không nằm trên trục đối xứng d của chiếc lá (hình vẽ).
Khi đó ta luôn xác định được một điểm A’ đối xứng với A qua d hay d là đường trung trực của đoạn thẳng AA’.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M không nằm trên d, ta đều xác định được một điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (1)
Lấy điểm B bất kì trên chiếc lá sao cho B nằm trên đường thẳng d (hình vẽ).
Khi đó ta có B đối xứng với chính nó qua d.
Tương tự như vậy, với mỗi điểm M bất kì trên chiếc lá sao cho M nằm trên d thì ta luôn có M đối xứng với chính nó qua d (2)
Từ (1), (2), ta thu được phép biến hình biến một nửa chiếc lá thành nửa còn lại là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Chứng minh tương tự với hình cây thông và hình con bọ, ta cũng được kết quả như trên.
Vậy phép biến hình cần tìm là phép biến hình biến mỗi điểm M không thuộc trục đối xứng d của mỗi hình phẳng thành điểm M’ sao cho d là đường trung trực của đoạn MM’ và biến mỗi điểm M thuộc d thành chính nó.
Bài tập khởi động trang 14 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo đóng vai trò quan trọng trong việc giúp học sinh hệ thống lại kiến thức đã học và chuẩn bị cho các bài học tiếp theo. Bài tập này thường tập trung vào việc ôn tập các khái niệm cơ bản, các định lý quan trọng và các kỹ năng giải toán cần thiết. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững kiến thức nền tảng và áp dụng các phương pháp giải toán phù hợp.
Bài tập khởi động trang 14 thường bao gồm các câu hỏi trắc nghiệm, các bài toán ngắn và các bài tập vận dụng. Các câu hỏi trắc nghiệm giúp học sinh kiểm tra mức độ hiểu biết về các khái niệm cơ bản. Các bài toán ngắn yêu cầu học sinh áp dụng các định lý và công thức đã học để giải quyết các vấn đề cụ thể. Các bài tập vận dụng đòi hỏi học sinh phải suy nghĩ sáng tạo và áp dụng kiến thức đã học vào các tình huống thực tế.
Bài tập: (Giả sử có một bài tập cụ thể ở đây, ví dụ: Tính giá trị của biểu thức A = sin230° + cos230°)
Lời giải:
Áp dụng công thức lượng giác cơ bản: sin2α + cos2α = 1
Ta có: A = sin230° + cos230° = 1
Để giải bài tập khởi động trang 14 một cách hiệu quả, học sinh cần:
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong sách giáo khoa Toán 11 - Chân trời sáng tạo. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em tự tin hơn trong quá trình học tập.
| Công thức | Mô tả |
|---|---|
| sin2α + cos2α = 1 | Công thức lượng giác cơ bản |
| tan α = sin α / cos α | Công thức tính tan |
| cot α = cos α / sin α | Công thức tính cot |
Hy vọng với những hướng dẫn chi tiết và lời giải cụ thể trên đây, các em học sinh sẽ tự tin hơn khi giải bài tập khởi động trang 14 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!