Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
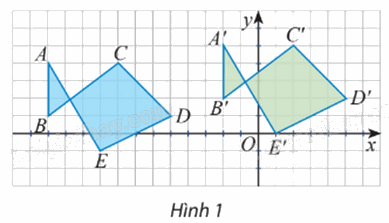
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).
Chứng minh phép đồng nhất là một phép tịnh tiến.
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
Giả sử A’ là ảnh của A qua phép đồng nhất f. Tức là, A’ = f(A).
Suy ra \(A'{\rm{ }} \equiv {\rm{ }}A\) hay \(AA'{\rm{ }} = {\rm{ }}0.\)
Khi đó \(\overrightarrow {AA'} = \vec 0\).
Tương tự như vậy, với mỗi điểm M bất kì, ta lấy điểm M’ là ảnh của điểm M qua phép đồng nhất f.
Khi đó ta cũng có \(\overrightarrow {MM'} = \vec 0\).
Vậy phép đồng nhất là một phép tịnh tiến theo \(\vec 0\)
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).
a) Có nhận xét gì về các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \)
b) Có hay không phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’?
Phương pháp giải:
Quan sát hình 1, nhận xét về hướng, độ dài của các vectơ
Lời giải chi tiết:
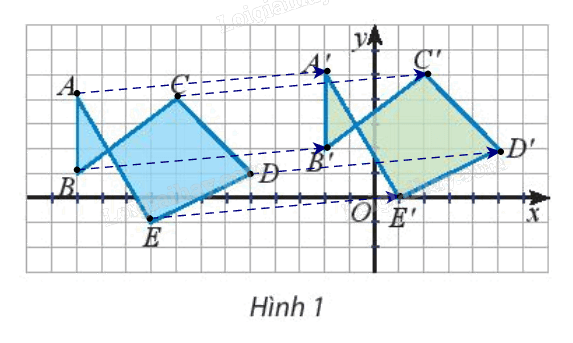
a) Quan sát Hình 1, ta thấy các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \) cùng hướng và có độ dài bằng nhau.
Vậy \(\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
b) Ta đặt \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
Khi đó tồn tại phép biến hình biến điểm A thành điểm A’ sao cho \(\overrightarrow {AA'} = {\rm{\vec u}}\)
Tương tự như vậy, ta thấy phép biến hình đó cũng biến các điểm B, C, D, E thành các điểm B’, C’, D’, E’ sao cho \(\overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} = {\rm{\vec u}}\)
Vậy có phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’
Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị).
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Lời giải chi tiết:
Từ Hoạt động khám phá 1, ta có \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \).
Ta đặt \({\rm{\vec v}} = {\rm{\vec u}}\)
Khi đó phép tịnh tiến theo \({\rm{\vec v}} = {\rm{\vec u}}\) biến các điểm A, B, C, D, E thành điểm A’, B’, C’, D’, E’.
Dựng \(\Delta AA'M\) vuông tại M (như hình vẽ).
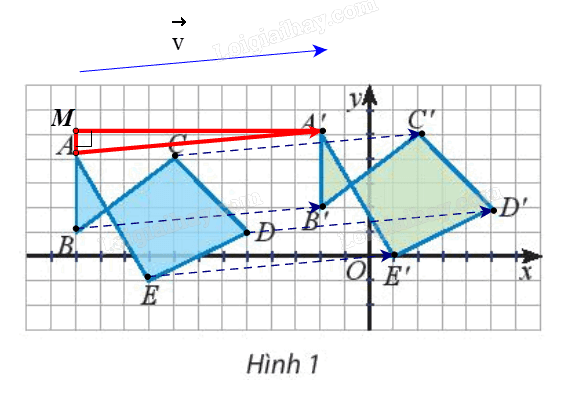
Ta có \(AM{\rm{ }} = {\rm{ }}1\) (đơn vị), \(A'M{\rm{ }} = {\rm{ }}10\) (đơn vị) (do cạnh mỗi ô vuông là 1 đơn vị).
Suy ra \(AA' = \sqrt {A{M^2} + {\rm{A'}}{{\rm{M}}^2}} = \sqrt {{1^2} + {{10}^2}} = \sqrt {101} \).
Khi đó \(\left| {{\rm{\vec v}}} \right| = \left| {\overrightarrow {AA'} } \right| = AA' = \sqrt {101} \)
Vậy độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) là \(\sqrt {101} \).
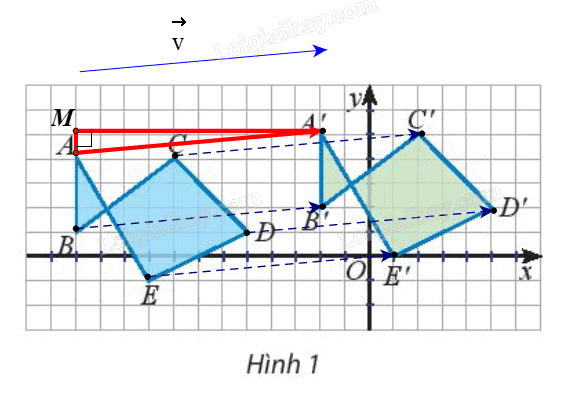
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).
a) Có nhận xét gì về các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \)
b) Có hay không phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’?
Phương pháp giải:
Quan sát hình 1, nhận xét về hướng, độ dài của các vectơ
Lời giải chi tiết:
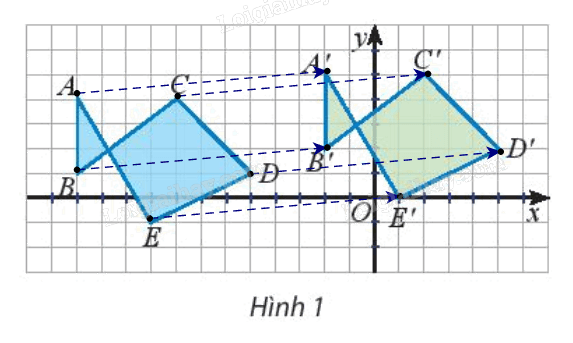
a) Quan sát Hình 1, ta thấy các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \) cùng hướng và có độ dài bằng nhau.
Vậy \(\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
b) Ta đặt \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \)
Khi đó tồn tại phép biến hình biến điểm A thành điểm A’ sao cho \(\overrightarrow {AA'} = {\rm{\vec u}}\)
Tương tự như vậy, ta thấy phép biến hình đó cũng biến các điểm B, C, D, E thành các điểm B’, C’, D’, E’ sao cho \(\overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} = {\rm{\vec u}}\)
Vậy có phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’
Chứng minh phép đồng nhất là một phép tịnh tiến.
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
Giả sử A’ là ảnh của A qua phép đồng nhất f. Tức là, A’ = f(A).
Suy ra \(A'{\rm{ }} \equiv {\rm{ }}A\) hay \(AA'{\rm{ }} = {\rm{ }}0.\)
Khi đó \(\overrightarrow {AA'} = \vec 0\).
Tương tự như vậy, với mỗi điểm M bất kì, ta lấy điểm M’ là ảnh của điểm M qua phép đồng nhất f.
Khi đó ta cũng có \(\overrightarrow {MM'} = \vec 0\).
Vậy phép đồng nhất là một phép tịnh tiến theo \(\vec 0\)
Tìm độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) biến các điểm A, B, C, D, E thành A’, B’, C’, D’, E’ trong Hoạt động khám phá 1 (biết cạnh mỗi ô vuông là 1 đơn vị).
Phương pháp giải:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Lời giải chi tiết:
Từ Hoạt động khám phá 1, ta có \({\rm{\vec u}} = \overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {CC'} = \overrightarrow {DD'} = \overrightarrow {EE'} \).
Ta đặt \({\rm{\vec v}} = {\rm{\vec u}}\)
Khi đó phép tịnh tiến theo \({\rm{\vec v}} = {\rm{\vec u}}\) biến các điểm A, B, C, D, E thành điểm A’, B’, C’, D’, E’.
Dựng \(\Delta AA'M\) vuông tại M (như hình vẽ).
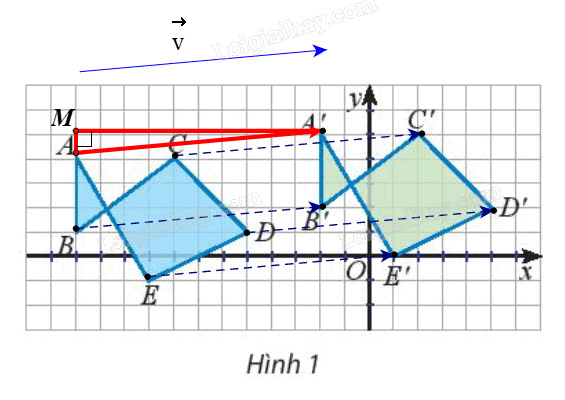
Ta có \(AM{\rm{ }} = {\rm{ }}1\) (đơn vị), \(A'M{\rm{ }} = {\rm{ }}10\) (đơn vị) (do cạnh mỗi ô vuông là 1 đơn vị).
Suy ra \(AA' = \sqrt {A{M^2} + {\rm{A'}}{{\rm{M}}^2}} = \sqrt {{1^2} + {{10}^2}} = \sqrt {101} \).
Khi đó \(\left| {{\rm{\vec v}}} \right| = \left| {\overrightarrow {AA'} } \right| = AA' = \sqrt {101} \)
Vậy độ dài vectơ tịnh tiến của phép tịnh tiến theo vectơ \({\rm{\vec v}}\) là \(\sqrt {101} \).
Mục 1 trang 11 trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một khái niệm hoặc kỹ năng nền tảng quan trọng. Việc nắm vững nội dung này là bước đệm cần thiết cho việc giải quyết các bài toán phức tạp hơn trong chương trình học. Bài viết này sẽ cung cấp một cái nhìn tổng quan về mục 1, phân tích các khái niệm chính và đưa ra phương pháp tiếp cận hiệu quả để giải các bài tập liên quan.
Để hiểu rõ hơn về Mục 1 trang 11, chúng ta cần xem xét các yếu tố sau:
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạo:
Lời giải: (Giải thích chi tiết từng bước giải bài tập 1, bao gồm các công thức, định lý được sử dụng và kết quả cuối cùng.)
Lời giải: (Giải thích chi tiết từng bước giải bài tập 2, bao gồm các công thức, định lý được sử dụng và kết quả cuối cùng.)
Lời giải: (Giải thích chi tiết từng bước giải bài tập 3, bao gồm các công thức, định lý được sử dụng và kết quả cuối cùng.)
Để giải các bài tập trong Mục 1 trang 11 một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Kiến thức được học trong Mục 1 trang 11 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của toán học, chẳng hạn như:
Để củng cố kiến thức và kỹ năng, bạn có thể luyện tập thêm các bài tập sau:
| Bài tập | Nguồn |
|---|---|
| Bài tập 1 | Sách bài tập Toán 11 |
| Bài tập 2 | Đề thi thử Toán 11 |
Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về Mục 1 trang 11 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc bạn học tập tốt!