Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về nội dung bài học.
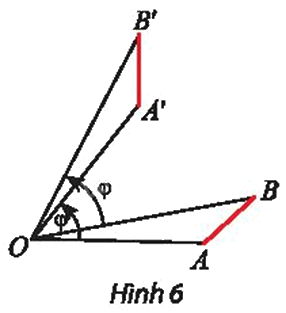
Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?
Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?
Phương pháp giải:
Quan sát hình 6 và xét các trường hợp bằng nhau của tam giác.
Lời giải chi tiết:
Ta có \({Q_{(O,{\rm{ }}\varphi )}}\) biến điểm A khác O thành điểm A’ sao cho \(OA{\rm{ }} = {\rm{ }}OA'\) và \(\left( {OA,{\rm{ }}OA'} \right){\rm{ }} = {\rm{ }}\varphi \;\) nên \(\widehat {AOA'} = \varphi \)
Tương tự, ta có \({Q_{\left( {O,{\rm{ }}\varphi } \right)}}\;\) biến điểm B khác O thành điểm B’ sao cho \(OB{\rm{ }} = {\rm{ }}OB'\) và \(\left( {OB,{\rm{ }}OB'} \right){\rm{ }} = {\rm{ }}\varphi \) nên \(\widehat {BO{B'}} = \varphi \)
Ta có \(\widehat {AOA'} = \widehat {BOB'}\left( { = \varphi } \right)\)
Suy ra \(\widehat {AOB} + \widehat {BOA'} = \widehat {BOA'} + \widehat {A'OB'}\)
Do đó \(\widehat {AOB} = \widehat {A'OB'}\)
Xét \(\Delta \) OAB và \(\Delta \) OA’B’, có:
OA = OA’ (chứng minh trên);
OB = OB’ (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (chứng minh trên).
Vậy \(\Delta \) OAB = \(\Delta \) OA’B’ (c.g.c).
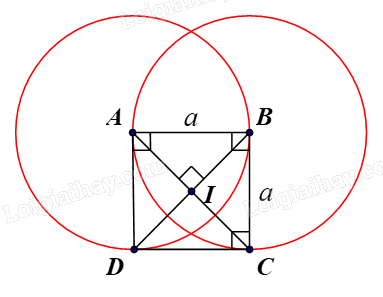
Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay \({Q_{(I,{\rm{ }}90^\circ )}}\;\) của các hình sau:
a) Tam giác IAB;
b) Đường thẳng BC;
c) Đường tròn (B, a).
Phương pháp giải:
Để tìm ảnh của một hình, đường thẳng qua phép quay, ta tìm ảnh của các điểm thuộc hình, đường thẳng đó qua phép quay. Sau đó nối chúng với nhau.
Lời giải chi tiết:

a) Hình vuông ABCD có tâm I.
Suy ra AC ⊥ BD tại I và IA = IB = IC = ID.
Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm I thành điểm I.
⦁ Điểm A thành điểm D;
⦁ Điểm B thành điểm A;
Vậy ảnh của tam giác IAB qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là tam giác IDA.
b) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm B thành điểm A;
⦁ Điểm C thành điểm B.
Vậy ảnh của đường thẳng BC qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường thẳng AB.
c) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) biến điểm B thành điểm A.
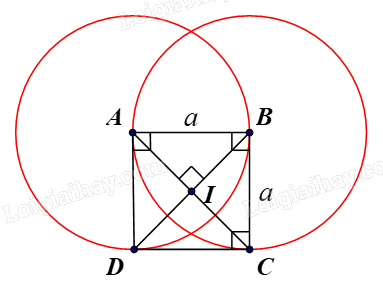
Vậy ảnh của đường tròn (B, a) qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường tròn (A, a).
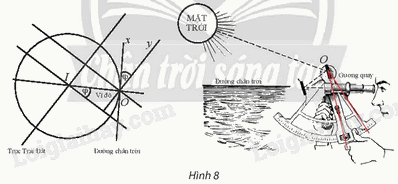
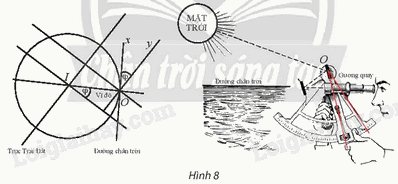
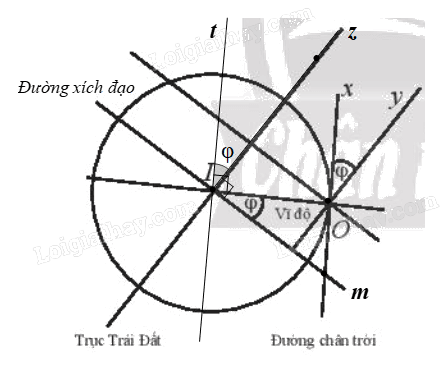
Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay \({Q_{(O,{\rm{ }}\varphi )}}\;\) biến tia Ox (song song với đường chân trời) thành tia Oy (song song với trục Trái Đất), nhờ đó đo được góc φ giữa trục của Trái Đất và đường chân trời tại vị trí của người đo. Hãy giải thích tại sao góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.
Phương pháp giải:
Quan sát hình 8 và suy luận để chứng minh
Lời giải chi tiết:
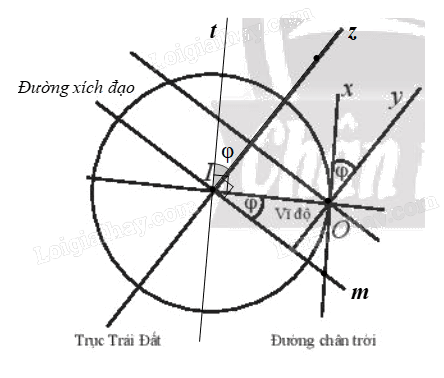
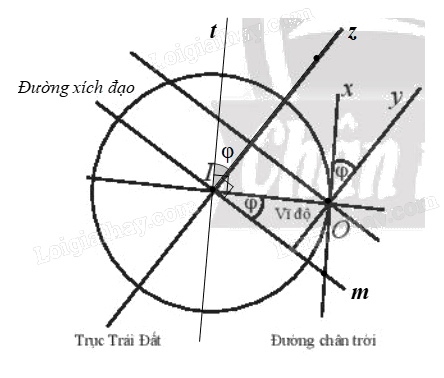
Gọi Iz là tia trùng với trục Trái Đất và nằm trên cùng một nửa mặt phẳng bờ IO chứa tia Ox, Oy.
Kẻ tia It song song với tia Ox.
Mà tia Oy song song với trục Trái Đất (giả thiết).
Do đó \(\widehat {tIz} = \widehat {xOy} = \varphi \)
Ta có tia Ox tiếp xúc với Trái Đất tại O.
Suy ra Ox là tiếp tuyến của đường tròn (I, IO).
Do đó \(Ox{\rm{ }} \bot {\rm{ }}IO.\)
Mà Ox // Ot nên \(Ot{\rm{ }} \bot {\rm{ }}IO.\)
Khi đó \(\widehat {tIz} + \widehat {zIO} = 90^\circ \,\,(1)\)
Gọi Im là tia trùng với đường xích đạo và nằm trên cùng một nửa mặt phẳng bờ Iz chứa đoạn thẳng IO.
Vì trục Trái Đất vuông góc với đường xích đạo nên ta có \(Iz \bot Im.\)
Suy ra \(\widehat {mIO} + \widehat {zIO} = 90^\circ \,\,(2)\)
Từ (1), (2), ta có \(\widehat {mIO} = \widehat {tIz} = \varphi \)
Vậy góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.
Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?
Phương pháp giải:
Quan sát hình 6 và xét các trường hợp bằng nhau của tam giác.
Lời giải chi tiết:
Ta có \({Q_{(O,{\rm{ }}\varphi )}}\) biến điểm A khác O thành điểm A’ sao cho \(OA{\rm{ }} = {\rm{ }}OA'\) và \(\left( {OA,{\rm{ }}OA'} \right){\rm{ }} = {\rm{ }}\varphi \;\) nên \(\widehat {AOA'} = \varphi \)
Tương tự, ta có \({Q_{\left( {O,{\rm{ }}\varphi } \right)}}\;\) biến điểm B khác O thành điểm B’ sao cho \(OB{\rm{ }} = {\rm{ }}OB'\) và \(\left( {OB,{\rm{ }}OB'} \right){\rm{ }} = {\rm{ }}\varphi \) nên \(\widehat {BO{B'}} = \varphi \)
Ta có \(\widehat {AOA'} = \widehat {BOB'}\left( { = \varphi } \right)\)
Suy ra \(\widehat {AOB} + \widehat {BOA'} = \widehat {BOA'} + \widehat {A'OB'}\)
Do đó \(\widehat {AOB} = \widehat {A'OB'}\)
Xét \(\Delta \) OAB và \(\Delta \) OA’B’, có:
OA = OA’ (chứng minh trên);
OB = OB’ (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (chứng minh trên).
Vậy \(\Delta \) OAB = \(\Delta \) OA’B’ (c.g.c).
Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay \({Q_{(I,{\rm{ }}90^\circ )}}\;\) của các hình sau:
a) Tam giác IAB;
b) Đường thẳng BC;
c) Đường tròn (B, a).
Phương pháp giải:
Để tìm ảnh của một hình, đường thẳng qua phép quay, ta tìm ảnh của các điểm thuộc hình, đường thẳng đó qua phép quay. Sau đó nối chúng với nhau.
Lời giải chi tiết:
a) Hình vuông ABCD có tâm I.
Suy ra AC ⊥ BD tại I và IA = IB = IC = ID.
Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm I thành điểm I.
⦁ Điểm A thành điểm D;
⦁ Điểm B thành điểm A;
Vậy ảnh của tam giác IAB qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là tam giác IDA.
b) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\)biến:
⦁ Điểm B thành điểm A;
⦁ Điểm C thành điểm B.
Vậy ảnh của đường thẳng BC qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường thẳng AB.
c) Ta có phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) biến điểm B thành điểm A.
Vậy ảnh của đường tròn (B, a) qua phép quay \({Q_{\left( {I,{\rm{ }}90^\circ } \right)}}\;\) là đường tròn (A, a).
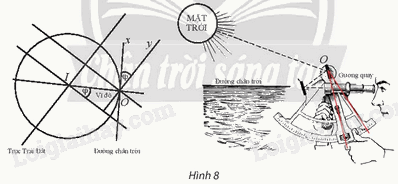
Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay \({Q_{(O,{\rm{ }}\varphi )}}\;\) biến tia Ox (song song với đường chân trời) thành tia Oy (song song với trục Trái Đất), nhờ đó đo được góc φ giữa trục của Trái Đất và đường chân trời tại vị trí của người đo. Hãy giải thích tại sao góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.
Phương pháp giải:
Quan sát hình 8 và suy luận để chứng minh
Lời giải chi tiết:
Gọi Iz là tia trùng với trục Trái Đất và nằm trên cùng một nửa mặt phẳng bờ IO chứa tia Ox, Oy.
Kẻ tia It song song với tia Ox.
Mà tia Oy song song với trục Trái Đất (giả thiết).
Do đó \(\widehat {tIz} = \widehat {xOy} = \varphi \)
Ta có tia Ox tiếp xúc với Trái Đất tại O.
Suy ra Ox là tiếp tuyến của đường tròn (I, IO).
Do đó \(Ox{\rm{ }} \bot {\rm{ }}IO.\)
Mà Ox // Ot nên \(Ot{\rm{ }} \bot {\rm{ }}IO.\)
Khi đó \(\widehat {tIz} + \widehat {zIO} = 90^\circ \,\,(1)\)
Gọi Im là tia trùng với đường xích đạo và nằm trên cùng một nửa mặt phẳng bờ Iz chứa đoạn thẳng IO.
Vì trục Trái Đất vuông góc với đường xích đạo nên ta có \(Iz \bot Im.\)
Suy ra \(\widehat {mIO} + \widehat {zIO} = 90^\circ \,\,(2)\)
Từ (1), (2), ta có \(\widehat {mIO} = \widehat {tIz} = \varphi \)
Vậy góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.
Mục 2 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Việc nắm vững kiến thức nền tảng và phương pháp giải quyết bài tập là yếu tố then chốt để đạt kết quả tốt. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 27 và 28, đồng thời phân tích các phương pháp tiếp cận hiệu quả.
Trang 27 thường chứa các bài tập vận dụng kiến thức đã học để giải quyết các vấn đề thực tế. Các bài tập này có thể bao gồm:
Ví dụ 1: Giải phương trình đạo hàm f'(x) = 0 để tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + 2.
Lời giải:
Trang 28 thường chứa các bài tập nâng cao, đòi hỏi học sinh phải vận dụng linh hoạt kiến thức và kỹ năng đã học. Các bài tập này có thể bao gồm:
Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x^4 - 2x^2 + 3 trên đoạn [-2, 2].
Lời giải:
Để giải quyết các bài tập trong mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo một cách hiệu quả, các em cần:
Việc giải bài tập mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo đòi hỏi sự kiên trì, nỗ lực và phương pháp học tập đúng đắn. Hy vọng rằng với lời giải chi tiết và các phương pháp tiếp cận hiệu quả được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc học tập và đạt kết quả tốt trong môn Toán.
| Chủ đề | Phương pháp |
|---|---|
| Hàm số | Xác định tập xác định, tập giá trị, tính đơn điệu, cực trị. |
| Đạo hàm | Tính đạo hàm, ứng dụng đạo hàm để giải quyết bài toán. |
| Giới hạn | Tính giới hạn, ứng dụng giới hạn để giải quyết bài toán. |