Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11 Chuyên đề học tập. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 6 trang 80, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 30a
Đề bài
Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 30a có hình biểu diễn được vẽ trên giấy kẻ ô li trên Hình 30b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 10 mm.
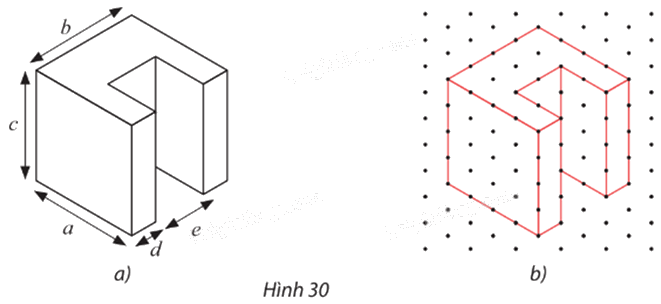
Phương pháp giải - Xem chi tiết
Dựa vào hình 30 để tìm các kích thước
Lời giải chi tiết
Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 30a được biểu diễn trên Hình 30b như sau:
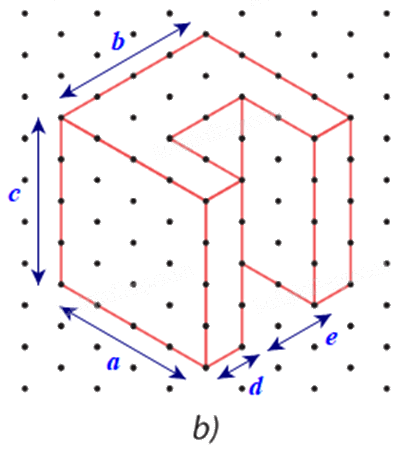
Do mỗi cạnh của tam giác đều biểu diễn độ dài 10 mm nên ta có:
Chiều dài a = 4.10 = 40 mm; chiều rộng b = 4.10 = 40 mm; chiều cao c = 4.10 = 40 mm; bề dày d = 1.10 = 10 mm; bề dày e = 2.10 = 20 mm.
Bài 6 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về đạo hàm, bao gồm đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị và khảo sát hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 6 trang 80 thường yêu cầu chúng ta tìm đạo hàm của một hàm số, hoặc sử dụng đạo hàm để giải quyết một bài toán liên quan đến tốc độ thay đổi của một đại lượng nào đó. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh những sai sót không đáng có.
Có nhiều phương pháp khác nhau để giải bài tập về đạo hàm, tùy thuộc vào dạng bài và yêu cầu cụ thể. Một số phương pháp phổ biến bao gồm:
Để cung cấp lời giải chi tiết cho bài 6 trang 80, chúng ta cần biết chính xác nội dung của bài toán. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số gợi ý về cách tiếp cận bài toán:
Ví dụ, nếu bài toán yêu cầu tìm đạo hàm của hàm số f(x) = x2 + 2x + 1, chúng ta có thể áp dụng quy tắc đạo hàm của hàm đa thức để tính đạo hàm như sau:
f'(x) = 2x + 2
Đạo hàm không chỉ là một công cụ toán học thuần túy, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau, như vật lý, kinh tế, kỹ thuật, và khoa học máy tính. Ví dụ, trong vật lý, đạo hàm được sử dụng để tính vận tốc và gia tốc của một vật thể. Trong kinh tế, đạo hàm được sử dụng để tính chi phí biên và doanh thu biên. Trong kỹ thuật, đạo hàm được sử dụng để tối ưu hóa các thiết kế và quy trình sản xuất.
Để nắm vững kiến thức về đạo hàm và rèn luyện kỹ năng giải bài tập, bạn nên luyện tập thêm các bài tập khác trong Chuyên đề học tập Toán 11 Chân trời sáng tạo, cũng như các bài tập từ các nguồn tài liệu khác. Bạn có thể tìm thấy các bài tập luyện tập trên giaitoan.edu.vn, hoặc trên các trang web và sách giáo khoa khác.
Bài 6 trang 80 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải bài tập. Hy vọng rằng, với hướng dẫn chi tiết và dễ hiểu trên đây, bạn đã có thể tự tin giải quyết bài toán này một cách hiệu quả. Chúc bạn học tập tốt!