Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 5 trang 90 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục kiến thức.
Hình, khối nào không được sử dụng để thiết kế chi tiết “đế đứng” có hình biểu diễn trong Hình 3.
Đề bài
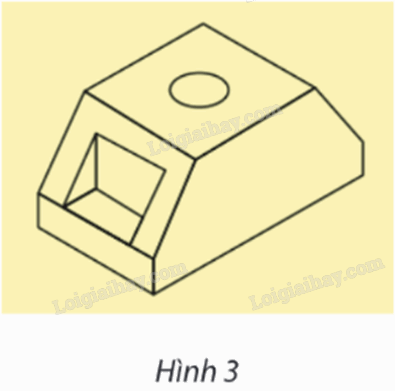
Hình, khối nào không được sử dụng để thiết kế chi tiết “đế đứng” có hình biểu diễn trong Hình 3.
A. Lăng trụ.
B. Hình hộp.
C. Hình chóp.
D. Hình trụ.
Phương pháp giải - Xem chi tiết
Dựa vào hình 3 để trả lời
Lời giải chi tiết
Đáp án đúng là: C
Các khối hình học tạo thành trong Hình 3 là: khối trụ rỗng tròn xoay, bốn khối lăng trụ đứng tam giác có đáy là tam giác vuông, khối hộp chữ nhật.
Do đó hình, khối chóp không được sử dụng để thiết kế chi tiết “đế đứng” có hình biểu diễn trong Hình 3.
Vậy ta chọn phương án C.
Bài 5 trang 90 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 5 trang 90 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5 trang 90, chúng ta sẽ đi vào phân tích từng dạng bài tập cụ thể.
Để tính đạo hàm của hàm số, ta cần áp dụng các quy tắc tính đạo hàm đã học, bao gồm:
Ví dụ: Cho hàm số y = x2 + 2x - 1. Tính đạo hàm y’.
Lời giải: y’ = 2x + 2
Để tìm cực trị của hàm số, ta thực hiện các bước sau:
Ví dụ: Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Lời giải:
Để xác định khoảng đơn điệu của hàm số, ta xét dấu đạo hàm y’ trên các khoảng xác định:
Ví dụ: Xác định khoảng đơn điệu của hàm số y = x2 - 4x + 3.
Lời giải:
Các bài toán ứng dụng thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các vấn đề thực tế, chẳng hạn như bài toán tối ưu hóa (tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số). Để giải các bài toán này, ta thường thực hiện các bước sau:
Bài 5 trang 90 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.