Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 20, 21 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, logic, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Cho điểm O. Gọi f là quy tắc xác định như sau:
Trong mặt phẳng tọa độ Oxy, cho các điểm I(1; 1), M(2; 2), N(0; –3) và P(–1; –2). Tìm tọa độ các điểm \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right),{\rm{ }}N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right),{\rm{ }}P'{\rm{ }} = {\rm{ }}{Đ_I}\left( P \right).\)
Phương pháp giải:
Nếu thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
+ Ta có \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right).\)
Suy ra I(1; 1) là trung điểm MM’ với M(2; 2).
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M} = 2.1 - 2 = 0\\{y_{M'}} = 2{y_I} - {y_M} = 2.1 - 2 = 0\end{array} \right.\)
Suy ra M’ có tọa độ là (0; 0).
+ Ta có \(N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right).\)
Suy ra I(1; 1) là trung điểm của NN’ với N(0; –3).
Do đó \(\left\{ \begin{array}{l}{x_{N'}} = 2{x_I} - {x_N} = 2.1 - 0 = 2\\{y_{N'}} = 2{y_I} - {y_N} = 2.1 + 3 = 5\end{array} \right.\)
Suy ra N’ có tọa độ là N’(2; 5).
+ Ta có \(P' = {\rm{ }}{Đ_I}\left( P \right).\)
Suy ra I(1; 1) là trung điểm PP’ với P(–1; –2).
Do đó \(\left\{ \begin{array}{l}{x_{P'}} = 2{x_I} - {x_P} = 2.1 + 1 = 3\\{y_{P'}} = 2{y_I} - {y_P} = 2.1 + 2 = 4\end{array} \right.\)
Suy ra P’ có tọa độ là P’(3; 4).
Vậy \(M'\left( {0;{\rm{ }}0} \right),{\rm{ }}N'\left( {2;{\rm{ }}5} \right),{\rm{ }}P'\left( {3;{\rm{ }}4} \right).\)
Cho điểm O. Gọi f là quy tắc xác định như sau:
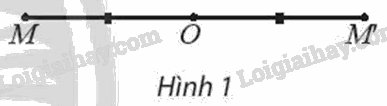
a) Với điểm M khác O, xác định điểm M’ sao cho O là trung điểm của MM’ (Hình 1).
b) Với điểm M trùng với O thì f biến điểm M thành chính nó.
Hỏi f có phải là phép biến hình không?
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
Theo đề, ta có M’ = f(M).
Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
Tìm phép đối xứng tâm biến mỗi hình sau thành chính nó.

Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
⦁ Ta xét hình màu đỏ:

Giả sử ta chọn điểm O trên hình màu đỏ như hình vẽ.
Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.
Lấy điểm A bất kì trên hình màu đỏ sao cho A ≠ O.
Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên hình màu đỏ, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến hình màu đỏ thành chính nó.
⦁ Ta xét hình màu xanh lá:
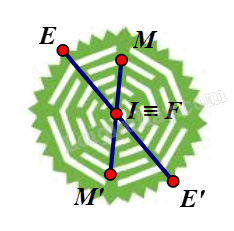
Giả sử ta chọn điểm I trên hình màu xanh lá như hình vẽ.
Lấy điểm F trùng I. Khi đó qua I, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên hình màu xanh lá sao cho E ≠ I.
Khi đó ta luôn xác định được một điểm E’ sao cho I là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác I trên hình màu xanh lá, ta đều xác định được một điểm M’ trên hình sao cho I là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm I biến hình màu xanh lá thành chính nó.
⦁ Ta xét hình màu xanh biển:
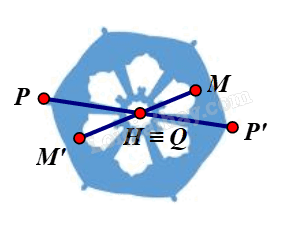
Giả sử ta chọn điểm H trên hình màu xanh biển như hình vẽ.
Lấy điểm P trùng H. Khi đó qua H, điểm đối xứng với P là chính nó.
Lấy điểm P bất kì trên hình màu xanh biển sao cho P ≠ H.
Khi đó ta luôn xác định được một điểm P’ sao cho H là trung điểm của đoạn PP’.
Tương tự như vậy, với mỗi điểm M bất kì khác H trên hình màu xanh biển, ta đều xác định được một điểm M’ trên hình sao cho H là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm H biến hình màu xanh biển thành chính nó.
Cho điểm O. Gọi f là quy tắc xác định như sau:
a) Với điểm M khác O, xác định điểm M’ sao cho O là trung điểm của MM’ (Hình 1).
b) Với điểm M trùng với O thì f biến điểm M thành chính nó.
Hỏi f có phải là phép biến hình không?

Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
Theo đề, ta có M’ = f(M).
Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
Trong mặt phẳng tọa độ Oxy, cho các điểm I(1; 1), M(2; 2), N(0; –3) và P(–1; –2). Tìm tọa độ các điểm \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right),{\rm{ }}N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right),{\rm{ }}P'{\rm{ }} = {\rm{ }}{Đ_I}\left( P \right).\)
Phương pháp giải:
Nếu thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
+ Ta có \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right).\)
Suy ra I(1; 1) là trung điểm MM’ với M(2; 2).
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M} = 2.1 - 2 = 0\\{y_{M'}} = 2{y_I} - {y_M} = 2.1 - 2 = 0\end{array} \right.\)
Suy ra M’ có tọa độ là (0; 0).
+ Ta có \(N'{\rm{ }} = {\rm{ }}{Đ_I}\left( N \right).\)
Suy ra I(1; 1) là trung điểm của NN’ với N(0; –3).
Do đó \(\left\{ \begin{array}{l}{x_{N'}} = 2{x_I} - {x_N} = 2.1 - 0 = 2\\{y_{N'}} = 2{y_I} - {y_N} = 2.1 + 3 = 5\end{array} \right.\)
Suy ra N’ có tọa độ là N’(2; 5).
+ Ta có \(P' = {\rm{ }}{Đ_I}\left( P \right).\)
Suy ra I(1; 1) là trung điểm PP’ với P(–1; –2).
Do đó \(\left\{ \begin{array}{l}{x_{P'}} = 2{x_I} - {x_P} = 2.1 + 1 = 3\\{y_{P'}} = 2{y_I} - {y_P} = 2.1 + 2 = 4\end{array} \right.\)
Suy ra P’ có tọa độ là P’(3; 4).
Vậy \(M'\left( {0;{\rm{ }}0} \right),{\rm{ }}N'\left( {2;{\rm{ }}5} \right),{\rm{ }}P'\left( {3;{\rm{ }}4} \right).\)
Tìm phép đối xứng tâm biến mỗi hình sau thành chính nó.

Phương pháp giải:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu . Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
⦁ Ta xét hình màu đỏ:
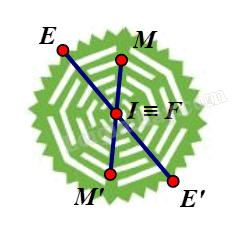
Giả sử ta chọn điểm O trên hình màu đỏ như hình vẽ.
Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.
Lấy điểm A bất kì trên hình màu đỏ sao cho A ≠ O.
Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.
Tương tự như vậy, với mỗi điểm M bất kì khác O trên hình màu đỏ, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm O biến hình màu đỏ thành chính nó.
⦁ Ta xét hình màu xanh lá:
Giả sử ta chọn điểm I trên hình màu xanh lá như hình vẽ.
Lấy điểm F trùng I. Khi đó qua I, điểm đối xứng với F là chính nó.
Lấy điểm E bất kì trên hình màu xanh lá sao cho E ≠ I.
Khi đó ta luôn xác định được một điểm E’ sao cho I là trung điểm của đoạn EE’.
Tương tự như vậy, với mỗi điểm M bất kì khác I trên hình màu xanh lá, ta đều xác định được một điểm M’ trên hình sao cho I là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm I biến hình màu xanh lá thành chính nó.
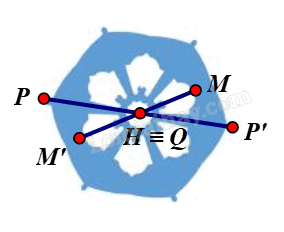
⦁ Ta xét hình màu xanh biển:
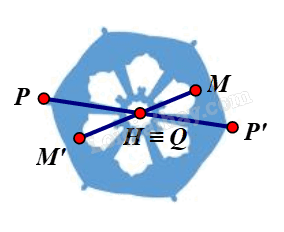
Giả sử ta chọn điểm H trên hình màu xanh biển như hình vẽ.
Lấy điểm P trùng H. Khi đó qua H, điểm đối xứng với P là chính nó.
Lấy điểm P bất kì trên hình màu xanh biển sao cho P ≠ H.
Khi đó ta luôn xác định được một điểm P’ sao cho H là trung điểm của đoạn PP’.
Tương tự như vậy, với mỗi điểm M bất kì khác H trên hình màu xanh biển, ta đều xác định được một điểm M’ trên hình sao cho H là trung điểm của đoạn MM’.
Vậy phép đối xứng tâm H biến hình màu xanh biển thành chính nó.
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một khái niệm hoặc kỹ năng toán học cụ thể. Trang 20 và 21 thường chứa các bài tập vận dụng và mở rộng kiến thức đã học. Việc giải các bài tập này không chỉ giúp học sinh củng cố lý thuyết mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Bài tập này thường yêu cầu học sinh áp dụng một định lý hoặc công thức đã học để giải quyết một bài toán cụ thể. Ví dụ, nếu mục 1 nói về hàm số bậc hai, bài tập có thể yêu cầu tìm đỉnh của parabol hoặc giải phương trình bậc hai. Lời giải cần trình bày rõ ràng các bước thực hiện, từ việc xác định dữ kiện đầu vào đến việc áp dụng công thức và kết luận.
Bài tập này có thể là một bài toán thực tế được mô hình hóa bằng toán học. Ví dụ, bài toán có thể liên quan đến việc tính toán diện tích, thể tích, hoặc tốc độ thay đổi của một đại lượng nào đó. Lời giải cần phân tích bài toán, xây dựng mô hình toán học, và giải mô hình đó để tìm ra kết quả.
Bài tập này thường là một bài tập nâng cao, yêu cầu học sinh kết hợp nhiều kiến thức và kỹ năng khác nhau để giải quyết. Ví dụ, bài tập có thể yêu cầu chứng minh một đẳng thức hoặc tìm điều kiện để một phương trình có nghiệm. Lời giải cần trình bày một cách chặt chẽ và logic, sử dụng các định lý và công thức đã học một cách chính xác.
Đề bài: Tìm tập xác định của hàm số y = √(x - 2).
Lời giải:
Hàm số y = √(x - 2) xác định khi và chỉ khi biểu thức dưới dấu căn không âm, tức là x - 2 ≥ 0. Điều này tương đương với x ≥ 2. Vậy tập xác định của hàm số là D = [2, +∞).
Việc giải các bài tập trong Chuyên đề học tập Toán 11 - Chân trời sáng tạo đòi hỏi sự hiểu biết sâu sắc về lý thuyết và kỹ năng giải toán. Bằng cách áp dụng các phương pháp giải bài tập hiệu quả và luyện tập thường xuyên, bạn có thể đạt được kết quả tốt trong môn Toán.