Bài 2 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chuyên đề. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo, đảm bảo hỗ trợ tối đa cho quá trình học tập của các em.
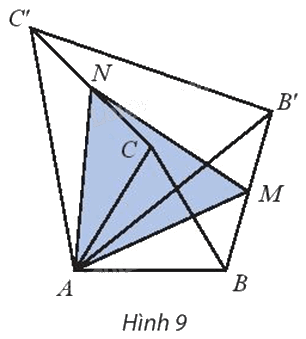
Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.
Đề bài
Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.
Phương pháp giải - Xem chi tiết
Tam giác cân có một góc bằng \({60^o}\) là tam giác đều.
Lời giải chi tiết
Do DABC là tam giác đều nên \(AB{\rm{ }} = {\rm{ }}AC\) và \(\widehat {BAC} = 60^\circ \)
Do DAB’C’ là tam giác đều nên \(AB'{\rm{ }} = {\rm{ }}AC'\) và \(\widehat {{\rm{B'}}AC'} = 60^\circ \)
Ta có phép quay tâm A, góc quay 60° biến:
⦁ Điểm B thành điểm C;
⦁ Điểm B’ thành điểm C’.
Do đó ảnh của đoạn thẳng BB’ qua phép quay tâm A, góc quay 60° là đoạn thẳng CC’.
Mà M, N lần lượt là trung điểm của BB’, CC’ (giả thiết).
Do đó phép quay tâm A, góc quay 60° biến điểm M thành điểm N.
Suy ra \(AM{\rm{ }} = {\rm{ }}AN\) và \(\widehat {MAN} = \left( {AM,AN} \right) = 60^\circ \)
DAMN có \(AM{\rm{ }} = {\rm{ }}AN\) và \(\widehat {MAN} = 60^\circ \) ° nên là tam giác đều.
Vậy ∆AMN đều.
Bài 2 trang 29 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo thường xoay quanh các chủ đề về hàm số, đồ thị hàm số, hoặc các ứng dụng của đạo hàm. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết và kỹ năng giải toán cơ bản.
Trước khi bắt đầu giải bài, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có. Ví dụ, đề bài có thể yêu cầu tìm tập xác định của hàm số, vẽ đồ thị hàm số, hoặc giải phương trình, bất phương trình.
Sau khi đã hiểu rõ yêu cầu của bài toán, hãy áp dụng các kiến thức lý thuyết đã học để giải bài. Ví dụ, nếu đề bài yêu cầu tìm tập xác định của hàm số, bạn cần nhớ các điều kiện để hàm số xác định (ví dụ: mẫu số khác 0, biểu thức dưới dấu căn lớn hơn hoặc bằng 0).
Ngoài kiến thức lý thuyết, bạn cũng cần sử dụng các kỹ năng giải toán cơ bản như biến đổi đại số, giải phương trình, bất phương trình, hoặc vẽ đồ thị hàm số. Việc rèn luyện kỹ năng giải toán thường xuyên sẽ giúp bạn tự tin hơn khi đối mặt với các bài tập khó.
Sau khi đã giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác. Bạn có thể thay thế các giá trị đã tìm được vào phương trình, bất phương trình, hoặc đồ thị hàm số để kiểm tra xem chúng có thỏa mãn điều kiện của bài toán hay không.
Đề bài: Cho hàm số y = f(x) = x2 - 4x + 3. Tìm tập xác định và vẽ đồ thị hàm số.
Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = f(x) = x2 - 4x + 3.
Để học tốt môn Toán 11 Chân trời sáng tạo, bạn cần:
Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn khi giải bài 2 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo và đạt kết quả tốt trong môn học.