Bài 4 trang 90 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng và kiến thức đã học trong chuyên đề. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em tự tin giải bài tập và nắm vững kiến thức Toán 11.
Chúng tôi luôn cập nhật đáp án nhanh chóng và chính xác, đồng thời cung cấp các phương pháp giải bài tập hiệu quả, giúp các em học tập tốt hơn.
Tính thể tích của cái nêm có hình chiếu trục đo vuông góc đều trong Hình 2, cho biết khoảng cách giữa hai chấm biểu diễn độ dài thật 1 dm.
Đề bài
Tính thể tích của cái nêm có hình chiếu trục đo vuông góc đều trong Hình 2, cho biết khoảng cách giữa hai chấm biểu diễn độ dài thật 1 dm.
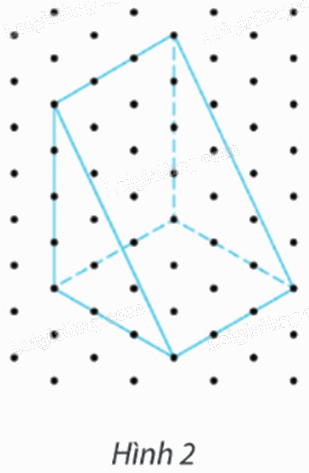
A. 36 dm3.
B. 24 dm3.
C. 18 dm3.
D. 9 dm3.
Phương pháp giải - Xem chi tiết
Thể tích khối lăng trụ: \(V = S.h\), S là diện tích đáy, h là chiều cao khối lăng trụ.
Lời giải chi tiết
Đáp án đúng là: C
Quan sát Hình 2, ta thấy khối lăng trụ đứng tam giác biểu diễn cái nêm có chiều cao 3 dm, tam giác đáy có kích thước hai cạnh góc vuông lần lượt là 3 dm và 4 dm.
Suy ra diện tích của tam giác đáy bằng: \(\frac{1}{2}.3.4 = 6\)\((d{m^2}).\)
Do đó thể tích của cái nêm đã cho bằng: \(6.3{\rm{ }} = {\rm{ }}18{\rm{ }}(d{m^3}).\)
Vậy ta chọn phương án C.
Bài 4 trang 90 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Bài 4 trang 90 thường yêu cầu học sinh thực hiện các bước sau:
Để giải bài 4 trang 90 Chuyên đề học tập Toán 11 Chân trời sáng tạo, chúng ta sẽ thực hiện theo các bước sau:
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2. Ta tính đạo hàm f'(x) như sau:
f'(x) = 3x2 - 6x
Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2.
Để xác định xem các điểm này là điểm cực đại hay cực tiểu, ta xét dấu của đạo hàm cấp hai f''(x):
f''(x) = 6x - 6
f''(0) = -6 < 0, vậy x = 0 là điểm cực đại.
f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.
Ta xét dấu của f'(x) trên các khoảng:
Để hiểu rõ hơn về cách giải bài 4 trang 90, chúng ta có thể xem xét một ví dụ minh họa khác. Giả sử hàm số là g(x) = x4 - 4x2 + 3. Thực hiện tương tự các bước trên, ta sẽ tìm được các điểm cực trị và khoảng đơn điệu của hàm số này.
Ngoài ra, các bạn có thể tự giải các bài tập tương tự trong sách giáo khoa và sách bài tập để rèn luyện kỹ năng giải toán. Một số bài tập tương tự có thể là:
Khi giải các bài tập về đạo hàm, các bạn cần lưu ý một số điểm sau:
Bài 4 trang 90 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết trên, các bạn sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán 11.