Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 89 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Đọc bản vẽ kĩ thuật trong Hình 16.
Đề bài
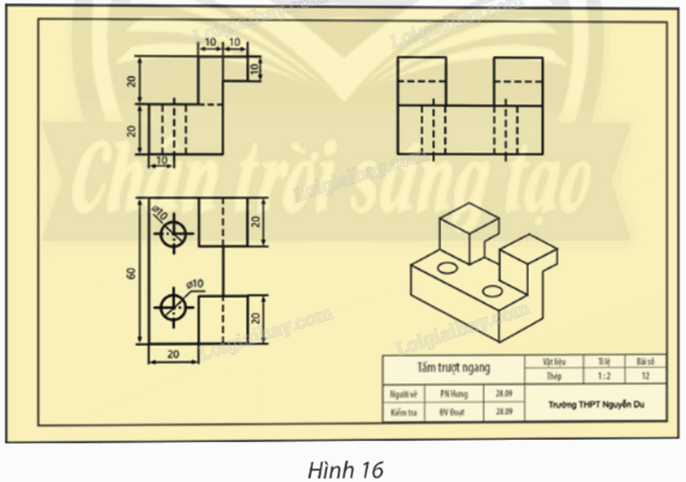
Đọc bản vẽ kĩ thuật trong Hình 16.
– Cho biết tên gọi của bản vẽ và tỉ lệ.
– Liệt kê các loại hình chiếu đã sử dụng.
– Liệt kê kích thước ba chiều của vật và kích thước các khối hình học tạo thành.
Phương pháp giải - Xem chi tiết
Dựa vào khung tên hình 16 để trả lời
Lời giải chi tiết
– Tên gọi của bản vẽ: Tấm trượt ngang.
– Tỉ lệ: 1:2.
– Có hai loại hình chiếu đã sử dụng: Hình chiếu vuông góc và hình chiếu trục đo.
– Liệt kê kích thước ba chiều của vật: chiều dài 60 cm, chiều rộng 40 cm, chiều cao 40 cm.
– Liệt kê kích thước các khối hình học tạo thành:
+ Hai khối trụ rỗng tròn xoay có đường kính 10 cm;
+ Khối hộp chữ nhật có chiều dài 60 cm, chiều rộng 20 cm, chiều cao 20 cm;
+ Khối hộp chữ nhật có chiều dài 60 cm, chiều rộng 10 cm, chiều cao 30 cm;
+ Khối hộp chữ nhật có chiều dài 20 cm, chiều rộng 10 cm, chiều cao 20 cm;
+ Khối hộp chữ nhật có chiều dài 20 cm, chiều rộng 10 cm, chiều cao 10 cm.
Bài 4 trang 89 Chuyên đề học tập Toán 11 Chân trời sáng tạo thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 4 trang 89, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập.
Lời giải:
Đặt u = x^2 + 1. Khi đó, y = sin(u).
Ta có: du/dx = 2x và dy/du = cos(u).
Áp dụng quy tắc đạo hàm hàm hợp, ta có:
dy/dx = (dy/du) * (du/dx) = cos(u) * 2x = 2x * cos(x^2 + 1).
Lời giải:
Đạo hàm cấp một: y' = 3x^2 - 4x.
Đạo hàm cấp hai: y'' = 6x - 4.
Lời giải:
Tính đạo hàm cấp một: y' = 3x^2 - 6x.
Tìm nghiệm của phương trình y' = 0: 3x^2 - 6x = 0 => x = 0 hoặc x = 2.
Lập bảng xét dấu y':
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| Hàm số | Đồng biến | Nghịch biến | Đồng biến |
Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Lời giải:
Tính đạo hàm cấp một: y' = 4x^3 - 8x.
Tìm nghiệm của phương trình y' = 0: 4x^3 - 8x = 0 => x = 0, x = √2, x = -√2.
Tính đạo hàm cấp hai: y'' = 12x^2 - 8.
Xét dấu y'' tại các điểm dừng:
Để giải các bài tập về đạo hàm một cách hiệu quả, các em cần:
Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em đã hiểu rõ hơn về cách giải bài 4 trang 89 Chuyên đề học tập Toán 11 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!