Bài 5 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Tìm đường đi ngắn nhất từ đỉnh A đến từng đỉnh (khác A) trong đồ thị có trọng số ở Hình 19.
Đề bài
Tìm đường đi ngắn nhất từ đỉnh A đến từng đỉnh (khác A) trong đồ thị có trọng số ở Hình 19.
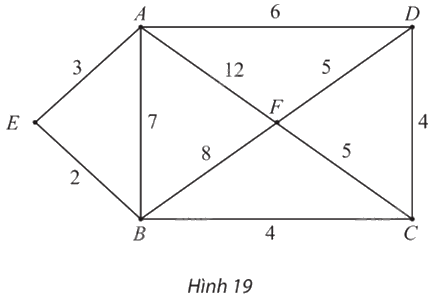
Phương pháp giải - Xem chi tiết
Thuật toán tìm đường đi ngắn nhất từ đỉnh A đến đỉnh T
Mở đầu: Gán nhãn của A bằng 0, các đỉnh khác bằng \(\infty \). Khoanh tròn đỉnh A.
Các bước lặp
Trong mỗi bước lặp thực hiện các thao tác sau đây:
- Gọi U là đỉnh vừa được khoanh tròn ở bước trước. Trong các đỉnh chưa khoanh tròn, xét lần lượt từng đỉnh V kề với đỉnh U, tính \({n_U}\; + {\rm{ }}{w_{UV}}\), rồi so sánh số này với nhãn hiện tại \({n_V}\;\) của V. Nếu số đó nhỏ hơn thì đổi nhãn \({n_V}\;\) bằng số đó.
- So sánh nhãn của tất cả các đỉnh chưa khoanh tròn. Đỉnh nào có nhãn nhỏ nhất thì khoanh tròn đỉnh đó (nếu có nhiều đỉnh hư vậy thì khoanh một đỉnh tùy ý trong số đó).
- Nếu đỉnh T chưa được khoanh tròn thì thực hiện bước lặp tiếp theo, trái lại thì kết thức các bước lặp.
Kết luận: Dò lại các bước lặp để viết được nhãn \({n_T}\) của T dưới dạng tổng độ dài các cạnh. Từ đó nhận được đường đi ngắn nhất từ A đến T cùng với độ dài của nó.
Lời giải chi tiết
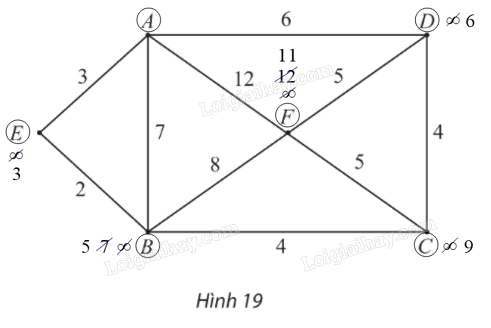
– Gán nhãn cho A bằng 0 (tức là, \({n_A}\; = {\rm{ }}0\)), các đỉnh khác bằng \(\infty \). Khoanh tròn đỉnh A.
– Tại các đỉnh kề với A, gồm E, B, D, F, ta có:
⦁ \({n_E}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}3\).Vì \(3{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của E thành 3.
⦁ \({n_B}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AB}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}7\).Vì \(7{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của B thành 7.
⦁ \({n_D}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}6\).Vì \(6{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của D thành 6.
⦁ \({n_F}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AF}}\; = {\rm{ }}0{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}12\).Vì \(12{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của F thành 12.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần A nhất, chỉ tính các đỉnh khác A).
Ta có \({n_E}\; = {\rm{ }}3{\rm{ }} = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; = {\rm{ }}{w_{AE}}\; = {\rm{ }}{l_{AE}}.\)
Vì vậy AE là đường đi ngắn nhất từ A đến E, với độ dài bằng 3.
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E chỉ có B, ta có:
\({n_B}\; = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}3{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}5\).Vì \(5{\rm{ }} < {\rm{ }}7\) (7 là nhãn hiện tại của B) nên ta đổi nhãn của B thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần A thứ hai).
Ta có \({n_B}\; = {\rm{ }}5{\rm{ }} = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; = {\rm{ }}{l_{AEB}}.\)
Vì vậy AEB là đường đi ngắn nhất từ A đến B, với độ dài bằng 5.
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B gồm F, C, ta có:
\({n_F}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BF}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}8{\rm{ }} = {\rm{ }}13\).Vì \(13{\rm{ }} > {\rm{ }}12\) (12 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 12.
\({n_C}\; = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}9.\)Vì \(9{\rm{ }} < {\rm{ }}\infty \) nên ta đổi nhãn của C thành 9.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là D nên ta khoanh tròn đỉnh D (đỉnh gần A thứ ba).
Ta có \({n_D}\; = {\rm{ }}6{\rm{ }} = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; = {\rm{ }}{w_{AD}}\; = {\rm{ }}{l_{AD}}.\)
Vì vậy AD là đường đi ngắn nhất từ đỉnh A đến D, với độ dài bằng 6.
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D gồm đỉnh F, C, ta có:
⦁ \({n_F}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}6{\rm{ }} + {\rm{ }}5{\rm{ }} = {\rm{ }}11.\)Vì \(11{\rm{ }} < {\rm{ }}12\) (12 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 11.
⦁ \({n_C}\; = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DC}}\; = {\rm{ }}6{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}10.\) Vì \(10{\rm{ }} > {\rm{ }}9\) (9 là nhãn hiện tại của C) nên ta giữ nguyên nhãn của C là 9.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh C nên ta khoanh tròn đỉnh C (đỉnh gần A thứ tư).
Ta có \({n_C}\; = {\rm{ }}9{\rm{ }} = {\rm{ }}{n_B}\; + {\rm{ }}{w_{BC}}\)
\(\begin{array}{*{20}{l}}{ = {\rm{ }}{n_E}\; + {\rm{ }}{w_{EB}}\; + {\rm{ }}{w_{BC}}}\\{ = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; + {\rm{ }}{w_{BC}}}\\{ = {\rm{ }}{w_{AE}}\; + {\rm{ }}{w_{EB}}\; + {\rm{ }}{w_{BC}}}\\{ = {\rm{ }}{l_{AEBC}}.}\end{array}\)
Vì vậy AEBC là đường đi ngắn nhất từ A đến C, với độ dài bằng 9.
– Lúc này, ta thấy chỉ còn đỉnh F chưa được khoanh tròn nên ta khoanh tròn đỉnh F (đỉnh gần A thứ năm).
Ta có \({n_F}\; = {\rm{ }}11{\rm{ }} = {\rm{ }}{n_D}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}{n_A}\; + {\rm{ }}{w_{AD}}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}{w_{AD}}\; + {\rm{ }}{w_{DF}}\; = {\rm{ }}{l_{ADF}}.\)
Vì vậy ADF là đường đi ngắn nhất từ A đến F, với độ dài bằng 11.
Vậy đường đi ngắn nhất từ đỉnh A đến các đỉnh B, C, D, E, F lần lượt là AEB, AEBC, AD, AE, ADF.
Bài 5 trang 66 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Cụ thể, bài toán yêu cầu học sinh xác định và tính toán đạo hàm của hàm số, sau đó sử dụng đạo hàm để tìm ra các giá trị cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết bài toán này một cách hiệu quả.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Đề bài thường cung cấp một hàm số cụ thể và yêu cầu chúng ta thực hiện một hoặc nhiều thao tác như:
Để giải quyết bài toán này, chúng ta cần áp dụng các công thức và quy tắc về đạo hàm đã học, bao gồm:
(Giả sử đề bài cụ thể là: Cho hàm số y = x3 - 3x2 + 2. Hãy tìm các điểm cực trị của hàm số.)
y' = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của đạo hàm cấp hai y'' = 6x - 6:
y(0) = 03 - 3(0)2 + 2 = 2
y(2) = 23 - 3(2)2 + 2 = -2
Kết luận: Hàm số đạt cực đại tại điểm (0; 2) và đạt cực tiểu tại điểm (2; -2).
Ngoài bài toán tìm điểm cực trị, bài 5 trang 66 và các bài tập tương tự còn có thể yêu cầu chúng ta:
Để giải quyết các bài toán này, chúng ta cần nắm vững các kiến thức về đạo hàm, khoảng đồng biến, nghịch biến, điểm uốn và cách vẽ đồ thị hàm số.
Bài 5 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.