Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong Chuyên đề học tập Toán 11, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 30, 31, 32 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Hãy cùng bắt đầu!
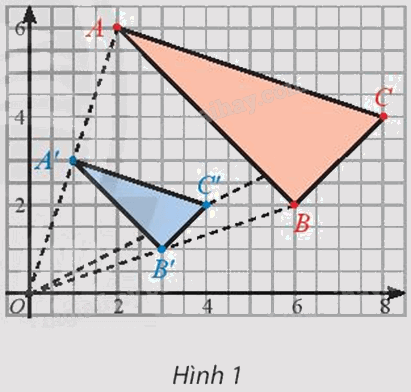
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; 9). Tìm tọa độ các điểm M1 và M2 lần lượt là ảnh của M qua các phép vị tự \({V_{\left( {O,{\rm{ }}3} \right)}}\;\) và \({V_{(O,{\rm{ }}-2)}}.\)
Phương pháp giải:
Nếu \({V_{(I,k)}}{\rm{[}}M(x,y){\rm{]}} = M'(x',y')\). Khi đó, \(\left\{ \begin{array}{l}x' - a = k(x - a)\\y' - b = k(y - b)\end{array} \right.\) với \(I(a;b)\)
Lời giải chi tiết:
Ta có \(\overrightarrow {OM} = \left( {3;9} \right)\)
⦁ Gọi \({M_1}({x_1};{\rm{ }}{y_1}),\;\) ta có \(\overrightarrow {O{M_1}} = \left( {{{\rm{x}}_1};{{\rm{y}}_1}} \right)\)
Theo đề, ta có \(\;{V_{(O,{\rm{ }}3)}}\left( M \right){\rm{ }} = {\rm{ }}{M_1}.\)
Suy ra \(\overrightarrow {O{M_1}} = 3\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_1} = 3.3 = 9}\\{{{\rm{y}}_1} = 3.9 = 27}\end{array}} \right.\)
Vì vậy tọa độ M1(9; 27).
⦁ Gọi \({M_2}({x_2};{\rm{ }}{y_2}),\;\) ta có \(\overrightarrow {O{M_2}} = \left( {{{\rm{x}}_2};{{\rm{y}}_2}} \right)\)
Theo đề, ta có \({V_{\left( {O,{\rm{ }}-2} \right)}}\left( M \right){\rm{ }} = {\rm{ }}{M_2}.\)
Suy ra \(\overrightarrow {O{M_2}} = - 2\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_2} = - 2.3 = - 6}\\{{{\rm{y}}_2} = - 2.9 = - 18}\end{array}} \right.\)
Vì vậy tọa độ \({M_2}\left( {-6;{\rm{ }}-18} \right).\)
Vậy \({M_1}\left( {9;{\rm{ }}27} \right),{M_2}\left( {-6;{\rm{ }}-18} \right).\)
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
a) Xét xem hai tam giác ABC và A’B’C’ đồng dạng không?
b) Thảo luận nhóm để tìm xem có phép biến hình nào biến tam giác ABC thành tam giác A’B’C’ không?
Phương pháp giải:
Quan sát hình 1 và chứng minh 2 tam giác đồng dạng theo trường hợp c.c.c
Lời giải chi tiết:
a) Ta có A’ là trung điểm của OA.
Suy ra \(OA' = \frac{1}{2}OA\) hay \(\frac{{OA'}}{{OA}} = \frac{1}{2}\)
Chứng minh tương tự, ta được \(\frac{{OB'}}{{OB}} = \frac{1}{2}\) và \(\frac{{OC'}}{{OC}} = \frac{1}{2}\)
Do \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\left( { = \frac{1}{2}} \right)\) nên áp dụng định lí Thales đảo, ta được A’B’ // AB.
Từ A’B’ // AB, theo hệ quả định lí Thales ta có: \(\frac{{A'B'}}{{AB}} = \frac{{OA'}}{{OA}} = \frac{1}{2}\) hay \(\frac{{AB}}{{A'B'}} = 2\)
Chứng minh tương tự, ta được \(\frac{{BC}}{{B'C'}} = 2\) và \(\frac{{AC}}{{A'C'}} = 2\)
Xét \(\Delta ABC{\rm{ }}\) và có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\left( { = 2} \right)\)
Vậy \(\Delta ABC\) đồng dạng với \(\Delta A\prime B\prime C\prime \) (c.c.c).
b) Để tìm phép biến hình biến ∆ABC thành ∆A’B’C’, ta tìm phép biến hình biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
Ta có A’ là trung điểm OA (giả thiết).
Suy ra \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \)
Do đó phép biến hình biến điểm A thành điểm A’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \,\,(1)\)
Thực hiện tương tự, ta được \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \)
Suy ra phép biến hình biến điểm B thành điểm B’ thỏa mãn \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \,\,(2)\)
Thực hiện tương tự, ta được \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \)
Do đó phép biến hình biến điểm C thành điểm C’ sao cho \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \,\,(3)\)
Từ (1), (2), (3), ta thu được phép biến hình biến \(\Delta ABC\) thành là phép biến hình biến ba điểm A, B, C thành ba điểm A’, B’, C’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} ,\,\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} ,\,\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \) với O là giao điểm của ba đường thẳng AA’, BB’, CC’.
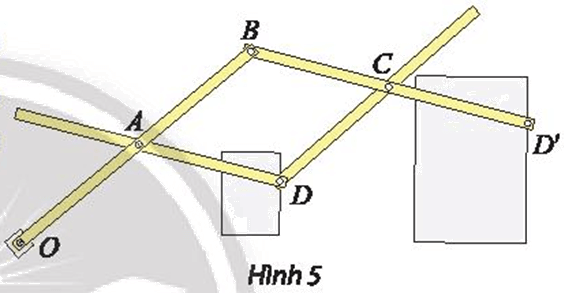
Thước vẽ truyền là một dụng cụ gồm bốn thanh gỗ hoặc kim loại được ghép với nhau nhờ bốn khớp xoay tại các điểm A, B, C, D sao cho ABCD là hình bình hành và ba điểm O, D, D’ thẳng hàng. Khi sử dụng, người vẽ ghim cố định điểm O xuống mặt giấy (thước vẫn có thể xoay quanh O). Đặt hai cây bút tại hai điểm D và D’. Khi đầu bút D vẽ hình ℋ, đầu bút D’ sẽ tự động vẽ truyền cho ta hình ℋ ’ là ảnh của ℋ.
a) Xác định tâm và tỉ số k của phép vị tự được sử dụng trong cây thước vẽ truyền ở Hình 5.
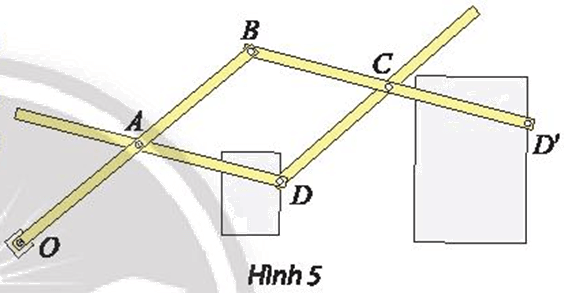
b) Nếu ngược lại cho đầu bút D’ vẽ hình ℋ ’ khi đó đầu bút D sẽ tự động vẽ truyền cho ta hình ℋ là ảnh của ℋ ’. Xác định phép vị tự trong trường hợp này.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
a) Do ba điểm O, D, D’ thẳng hàng (giả thiết), suy ra \(\overrightarrow {OD'} = k\overrightarrow {OD} \)
Do đó \({V_{(O,{\rm{ }}k)}}\left( D \right){\rm{ }} = {\rm{ }}D'\) và \(OD'{\rm{ }} = {\rm{ }}\left| k \right|.OD.\)
Vì D, D’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0.\)
Suy ra \(k = \frac{{OD'}}{{OD}}\)
Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).
Khi đó áp dụng định lí Thales, ta được \(k = \frac{{OD}}{{OD'}} = \frac{{OA}}{{OB}}\)
Vậy phép vị tự cần tìm là \({V_{\left( {O,\frac{{OA}}{{OB}}} \right)}}\)
b) Từ câu a, ta có \(\overrightarrow {OD'} = k\overrightarrow {OD} \,\,\left( {k{\rm{ }} > {\rm{ }}0} \right).\)
Suy ra \(\overrightarrow {OD} = \frac{1}{k}\overrightarrow {OD'} \)
Khi đó \({V_{\left( {O,\frac{1}{k}} \right)}}\left( {D'} \right) = D\)
Ta có \(\frac{1}{k} = 1:\frac{{OA}}{{OB}} = \frac{{OB}}{{OA}}\)
Vậy phép vị tự cần tìm là \({{\rm{V}}_{\left( {O,\frac{{OB}}{{OA}}} \right)}}\)
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
a) Xét xem hai tam giác ABC và A’B’C’ đồng dạng không?
b) Thảo luận nhóm để tìm xem có phép biến hình nào biến tam giác ABC thành tam giác A’B’C’ không?
Phương pháp giải:
Quan sát hình 1 và chứng minh 2 tam giác đồng dạng theo trường hợp c.c.c
Lời giải chi tiết:
a) Ta có A’ là trung điểm của OA.
Suy ra \(OA' = \frac{1}{2}OA\) hay \(\frac{{OA'}}{{OA}} = \frac{1}{2}\)
Chứng minh tương tự, ta được \(\frac{{OB'}}{{OB}} = \frac{1}{2}\) và \(\frac{{OC'}}{{OC}} = \frac{1}{2}\)
Do \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\left( { = \frac{1}{2}} \right)\) nên áp dụng định lí Thales đảo, ta được A’B’ // AB.
Từ A’B’ // AB, theo hệ quả định lí Thales ta có: \(\frac{{A'B'}}{{AB}} = \frac{{OA'}}{{OA}} = \frac{1}{2}\) hay \(\frac{{AB}}{{A'B'}} = 2\)
Chứng minh tương tự, ta được \(\frac{{BC}}{{B'C'}} = 2\) và \(\frac{{AC}}{{A'C'}} = 2\)
Xét \(\Delta ABC{\rm{ }}\) và có:
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\left( { = 2} \right)\)
Vậy \(\Delta ABC\) đồng dạng với \(\Delta A\prime B\prime C\prime \) (c.c.c).
b) Để tìm phép biến hình biến ∆ABC thành ∆A’B’C’, ta tìm phép biến hình biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
Ta có A’ là trung điểm OA (giả thiết).
Suy ra \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \)
Do đó phép biến hình biến điểm A thành điểm A’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} \,\,(1)\)
Thực hiện tương tự, ta được \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \)
Suy ra phép biến hình biến điểm B thành điểm B’ thỏa mãn \(\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} \,\,(2)\)
Thực hiện tương tự, ta được \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \)
Do đó phép biến hình biến điểm C thành điểm C’ sao cho \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \,\,(3)\)
Từ (1), (2), (3), ta thu được phép biến hình biến \(\Delta ABC\) thành là phép biến hình biến ba điểm A, B, C thành ba điểm A’, B’, C’ thỏa mãn \(\overrightarrow {OA'} = \frac{1}{2}\overrightarrow {OA} ,\,\overrightarrow {OB'} = \frac{1}{2}\overrightarrow {OB} ,\,\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \) với O là giao điểm của ba đường thẳng AA’, BB’, CC’.
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; 9). Tìm tọa độ các điểm M1 và M2 lần lượt là ảnh của M qua các phép vị tự \({V_{\left( {O,{\rm{ }}3} \right)}}\;\) và \({V_{(O,{\rm{ }}-2)}}.\)
Phương pháp giải:
Nếu \({V_{(I,k)}}{\rm{[}}M(x,y){\rm{]}} = M'(x',y')\). Khi đó, \(\left\{ \begin{array}{l}x' - a = k(x - a)\\y' - b = k(y - b)\end{array} \right.\) với \(I(a;b)\)
Lời giải chi tiết:
Ta có \(\overrightarrow {OM} = \left( {3;9} \right)\)
⦁ Gọi \({M_1}({x_1};{\rm{ }}{y_1}),\;\) ta có \(\overrightarrow {O{M_1}} = \left( {{{\rm{x}}_1};{{\rm{y}}_1}} \right)\)
Theo đề, ta có \(\;{V_{(O,{\rm{ }}3)}}\left( M \right){\rm{ }} = {\rm{ }}{M_1}.\)
Suy ra \(\overrightarrow {O{M_1}} = 3\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_1} = 3.3 = 9}\\{{{\rm{y}}_1} = 3.9 = 27}\end{array}} \right.\)
Vì vậy tọa độ M1(9; 27).
⦁ Gọi \({M_2}({x_2};{\rm{ }}{y_2}),\;\) ta có \(\overrightarrow {O{M_2}} = \left( {{{\rm{x}}_2};{{\rm{y}}_2}} \right)\)
Theo đề, ta có \({V_{\left( {O,{\rm{ }}-2} \right)}}\left( M \right){\rm{ }} = {\rm{ }}{M_2}.\)
Suy ra \(\overrightarrow {O{M_2}} = - 2\overrightarrow {OM} \)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{x}}_2} = - 2.3 = - 6}\\{{{\rm{y}}_2} = - 2.9 = - 18}\end{array}} \right.\)
Vì vậy tọa độ \({M_2}\left( {-6;{\rm{ }}-18} \right).\)
Vậy \({M_1}\left( {9;{\rm{ }}27} \right),{M_2}\left( {-6;{\rm{ }}-18} \right).\)
Thước vẽ truyền là một dụng cụ gồm bốn thanh gỗ hoặc kim loại được ghép với nhau nhờ bốn khớp xoay tại các điểm A, B, C, D sao cho ABCD là hình bình hành và ba điểm O, D, D’ thẳng hàng. Khi sử dụng, người vẽ ghim cố định điểm O xuống mặt giấy (thước vẫn có thể xoay quanh O). Đặt hai cây bút tại hai điểm D và D’. Khi đầu bút D vẽ hình ℋ, đầu bút D’ sẽ tự động vẽ truyền cho ta hình ℋ ’ là ảnh của ℋ.
a) Xác định tâm và tỉ số k của phép vị tự được sử dụng trong cây thước vẽ truyền ở Hình 5.
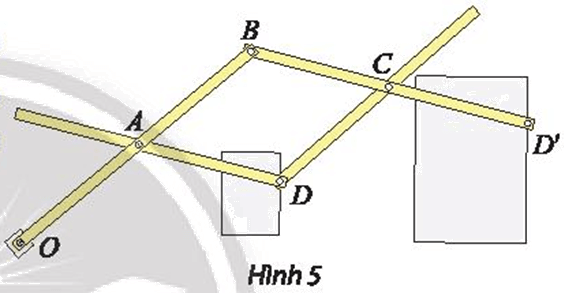
b) Nếu ngược lại cho đầu bút D’ vẽ hình ℋ ’ khi đó đầu bút D sẽ tự động vẽ truyền cho ta hình ℋ là ảnh của ℋ ’. Xác định phép vị tự trong trường hợp này.
Phương pháp giải:
Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Lời giải chi tiết:
a) Do ba điểm O, D, D’ thẳng hàng (giả thiết), suy ra \(\overrightarrow {OD'} = k\overrightarrow {OD} \)
Do đó \({V_{(O,{\rm{ }}k)}}\left( D \right){\rm{ }} = {\rm{ }}D'\) và \(OD'{\rm{ }} = {\rm{ }}\left| k \right|.OD.\)
Vì D, D’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0.\)
Suy ra \(k = \frac{{OD'}}{{OD}}\)
Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).
Khi đó áp dụng định lí Thales, ta được \(k = \frac{{OD}}{{OD'}} = \frac{{OA}}{{OB}}\)
Vậy phép vị tự cần tìm là \({V_{\left( {O,\frac{{OA}}{{OB}}} \right)}}\)
b) Từ câu a, ta có \(\overrightarrow {OD'} = k\overrightarrow {OD} \,\,\left( {k{\rm{ }} > {\rm{ }}0} \right).\)
Suy ra \(\overrightarrow {OD} = \frac{1}{k}\overrightarrow {OD'} \)
Khi đó \({V_{\left( {O,\frac{1}{k}} \right)}}\left( {D'} \right) = D\)
Ta có \(\frac{1}{k} = 1:\frac{{OA}}{{OB}} = \frac{{OB}}{{OA}}\)
Vậy phép vị tự cần tìm là \({{\rm{V}}_{\left( {O,\frac{{OB}}{{OA}}} \right)}}\)
Mục 1 của Chuyên đề học tập Toán 11 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt vào giải bài tập. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để đạt kết quả tốt.
Trước khi đi vào giải bài tập, chúng ta cần xác định rõ nội dung chính của Mục 1. Thông thường, mục này sẽ giới thiệu các khái niệm mới, định lý quan trọng và các ví dụ minh họa. Việc đọc kỹ sách giáo khoa và ghi chép đầy đủ là bước chuẩn bị quan trọng.
Bài 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng từng bước và kết luận). Lưu ý: (Ghi chú quan trọng liên quan đến bài tập).
Bài 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng từng bước và kết luận). Lưu ý: (Ghi chú quan trọng liên quan đến bài tập).
Bài 3: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng từng bước và kết luận). Lưu ý: (Ghi chú quan trọng liên quan đến bài tập).
Bài 4: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng từng bước và kết luận). Lưu ý: (Ghi chú quan trọng liên quan đến bài tập).
Bài 5: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng từng bước và kết luận). Lưu ý: (Ghi chú quan trọng liên quan đến bài tập).
Bài 6: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng từng bước và kết luận). Lưu ý: (Ghi chú quan trọng liên quan đến bài tập).
Bài 7: (Nêu lại đề bài). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng từng bước và kết luận). Lưu ý: (Ghi chú quan trọng liên quan đến bài tập).
Để hiểu sâu hơn về các khái niệm trong Mục 1, các em có thể tham khảo thêm các tài liệu sau:
Để củng cố kiến thức, các em nên tự giải thêm các bài tập tương tự. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Hy vọng với hướng dẫn chi tiết này, các em đã có thể tự giải các bài tập trong mục 1 trang 30, 31, 32 Chuyên đề học tập Toán 11 - Chân trời sáng tạo. Chúc các em học tập tốt!
Dạng bài tập: Tính giá trị của biểu thức...
Cách giải: (Giải thích cách giải, đưa ra các bước thực hiện cụ thể và ví dụ minh họa).
Khi giải bài tập Toán 11, các em cần chú ý đến các dấu hiệu nhận biết, các công thức và định lý liên quan. Việc vẽ hình minh họa cũng rất quan trọng, giúp các em hình dung rõ hơn về bài toán.
Hãy dành thời gian ôn tập lý thuyết thường xuyên và làm bài tập đầy đủ. Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè.