Bài 5 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn AB’ và nằm ngoài đoạn A’B
Đề bài
Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn AB’ và nằm ngoài đoạn A’B. Gọi G và G’ lần lượt là trọng tâm của \(\Delta \)OAA’ và \(\Delta \)OBB’. Chứng minh rằng \(\Delta \)OGG’ là tam giác vuông cân.
Phương pháp giải - Xem chi tiết
Tam giác vuông cân là tam giác có một góc bằng \({90^o}\) và 2 cạnh góc vuông bằng nhau.
Lời giải chi tiết
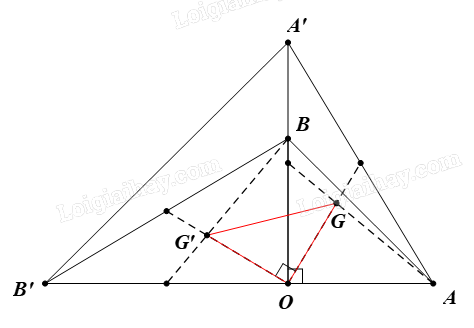
Do DOAB là tam giác vuông cân nên OA = OB và \(\widehat {AOB} = 90^\circ \)
Do DOA’B’ là tam giác vuông cân nên OA’ = OB’ và \(\widehat {A'OB'} = 90^\circ \)
Phép quay tâm O, góc quay 90° biến:
⦁ Điểm O thành điểm O;
⦁ Điểm A thành điểm B;
⦁ Điểm A’ thành điểm B’.
Do đó ảnh của \(\Delta \) OAA’ qua phép quay tâm O, góc quay 90° là \(\Delta \) OBB’.
Mà G, G’ lần lượt là trọng tâm của \(\;\Delta OAA',{\rm{ }}\Delta OBB'.\)
Vì vậy ảnh của G qua phép quay tâm O, góc quay 90° là G’.
Suy ra \(OG{\rm{ }} = {\rm{ }}OG'\) và \(\widehat {GOG'} = \left( {OG,OG'} \right) = 90^\circ \)
DOGG’ có \(OG{\rm{ }} = {\rm{ }}OG'\) và \(\widehat {GOG'} = 90^\circ \) nên là tam giác vuông cân tại O.
Vậy \(\Delta OGG'\) vuông cân tại O.
Bài 5 trang 29 thuộc Chuyên đề học tập Toán 11 Chân trời sáng tạo tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Cụ thể, bài toán yêu cầu học sinh xác định và tính toán đạo hàm của hàm số, sau đó sử dụng đạo hàm để tìm ra các giá trị cực trị hoặc giải quyết các bài toán tối ưu hóa đơn giản.
Để giải bài 5 trang 29 hiệu quả, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài toán thường bao gồm các bước sau:
(Giả sử đề bài là: Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Bước 1: Tính đạo hàm
f'(x) = 3x2 - 6x
Bước 2: Tìm điểm cực trị
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Bước 3: Xác định loại cực trị
Tính đạo hàm cấp hai:
f''(x) = 6x - 6
Tại x = 0: f''(0) = -6 < 0, vậy hàm số đạt cực đại tại x = 0.
Tại x = 2: f''(2) = 6 > 0, vậy hàm số đạt cực tiểu tại x = 2.
Bước 4: Kết luận
Hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là f(0) = 2.
Hàm số f(x) = x3 - 3x2 + 2 đạt cực tiểu tại x = 2 với giá trị là f(2) = -2.
Ngoài bài 5 trang 29, Chuyên đề học tập Toán 11 Chân trời sáng tạo còn có nhiều bài tập tương tự liên quan đến ứng dụng đạo hàm. Các bài tập này có thể yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức và phương pháp đã trình bày ở trên, đồng thời luyện tập thường xuyên để nâng cao kỹ năng giải toán.
Ngoài sách giáo khoa và sách bài tập, học sinh có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải bài 5 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo sẽ giúp các em học sinh học tập hiệu quả và đạt kết quả tốt trong môn Toán.